1.2.2 相反数 课件 (共16张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 1.2.2 相反数 课件 (共16张PPT)初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 869.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 18:15:35 | ||
图片预览






文档简介
(共16张PPT)
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.2 相反数
学习目标
1.借助数轴理解相反数的意义,了解一对相反数在数轴上 的位置关系;(难点)
2.会求给定有理数的相反数;(重点)
3.通过从数与形两方面了解相反数,初步体会数形结合的 思想方法.
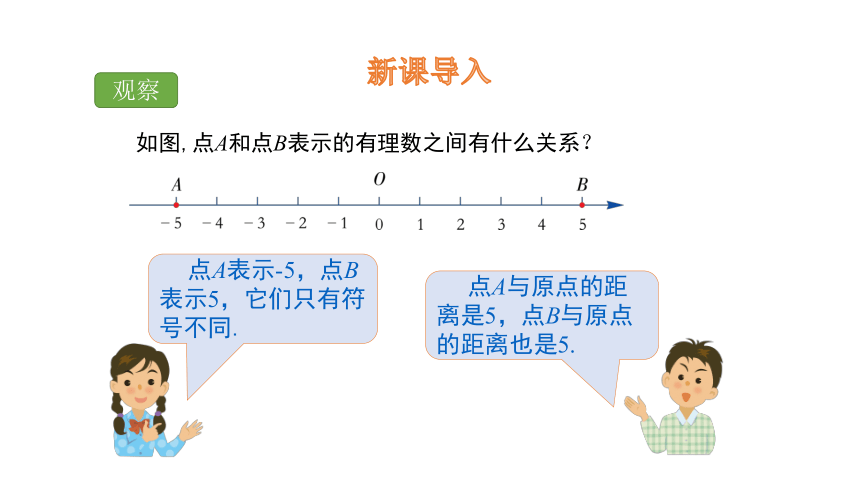
观察
如图,点A和点B表示的有理数之间有什么关系?
点A与原点的距离是5,点B与原点的距离也是5.
点A表示-5,点B表示5,它们只有符号不同.
新课导入
请观察这两个数,它们有什么异同点?
数字相同
符号不同
你还能列举
两个这样的
数吗?
像5和-5这样,如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数,也称这两个数互为相反数.
例如,2.6的相反数是-2.6,-2.6的相反数是2.6.
我们把数a的相反数记做-a.于是“-2.6 的相反数是2.6”就可以记做“-(-2.6)= 2.6”.
探究新知
特别地,0的相反数是0.
表示互为相反数的两个数的点,在数轴上分别位于原点的两侧,并且与原点的距离相等.
注意
例 3
例题讲解
画一条数轴,并标出表示下列各数的相反数的点:
3,1.5,-6.
解:3的相反数是-3;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如图所示.
1.代数意义:如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数.数a的相反数记作-a.特别地,0的相反数是0.
2.几何意义:表示互为相反数的两个点,在数轴上分别位于原点的两侧,并且与原点的距离相等.
3.-a表示a的相反数.因此,在这个数的前面添上“-”号,就得到这个数的相反数.正数的“+”号可省略不写,因此,在一个数前面添上“+”号,表示这个数本身.
4.正数的相反数是负数,负数的相反数是正数,0的相反数是0.
总结
补充练习
1.判断题,看谁回答的又对又快!
(1)-10是10的相反数. ( )
(2)10是10的相反数. ( )
(3)1.5与-1.5互为相反数.( )
(4)-2是相反数. ( )
×
√
√
×
2.(1)数轴上离原点3个单位长度的点所表示的数是________,它们的关系为____________.
(2)在数轴上,若点A和点B分别表示互为相反数的两个数,点A在点B的左侧,并且这两个数的距离是12.8,则A=______,B=______.
3或-3
互为相反数
-6.4
6.4
说一说
-(+1)= -(-1)=
因为-1的相反数是1,所以-(-1)=1.
因为+1的相反数是-1,所以-(+1)=-1.
例 4
例题讲解
填空:-(+0.8)= ;-(-3)= .
-0.8
3
注意:
+a的相反数是-a,记作-(+a)=-a;
-a的相反数是+a,记作-(-a)=+a.
这里a可表示正数,负数和0.
总结
2.对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.如果有奇数个“-”号,结果的符号就是“-”号;如果有偶数个“-”号,结果的符号就是“+”号.
1.在一个数前面加上“-”号表示这个数的相反数;在一个数前面加上“+”仍表示这个数,“+”号可省略.
补充练习
1、化简下列各数的符号:
(1)-(+3); (2)+(-1);
(3)+(+); (4)-[-(+3.5)];
(5)-{-[+(-)]}; (6)-[-(-a)].
解:(1)-(+3)=-3; (2)+(-1)=-1;
(3)+(+)=; (4)-[-(+3.5)]=3.5;
(5)-{-[+(-)]}=-; (6)-[-(-a)]=-a.
2.(1)若+5前面有2 022个负号,化简后结果是多少?
(2)若-5前面有2 023个负号,化简后结果是多少?你能总结出什么规律?
解:(1)若+5前面有2 022个负号,化简后结果是+5.
(2)若-5前面有2 023个负号,化简后结果+5.
总结规律:若一个数的前面有奇数个负号,则化简的结果等于它的相反数;若一个数的前面有偶数个负号,则化简的结果等于它本身.
课堂小结
1.相反数
(1)定义:只有符号不同的两个数互为相反数.
(2)代数意义:a的相反数是-a,0的相反数是0.
(3)几何意义:互为相反数的两个点到原点的距离相等.
2.多重符号的化简
(1)偶数个“-”号,结果为正数.
(2)奇数个“-”号,结果为负数.
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.2 相反数
学习目标
1.借助数轴理解相反数的意义,了解一对相反数在数轴上 的位置关系;(难点)
2.会求给定有理数的相反数;(重点)
3.通过从数与形两方面了解相反数,初步体会数形结合的 思想方法.
观察
如图,点A和点B表示的有理数之间有什么关系?
点A与原点的距离是5,点B与原点的距离也是5.
点A表示-5,点B表示5,它们只有符号不同.
新课导入
请观察这两个数,它们有什么异同点?
数字相同
符号不同
你还能列举
两个这样的
数吗?
像5和-5这样,如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数,也称这两个数互为相反数.
例如,2.6的相反数是-2.6,-2.6的相反数是2.6.
我们把数a的相反数记做-a.于是“-2.6 的相反数是2.6”就可以记做“-(-2.6)= 2.6”.
探究新知
特别地,0的相反数是0.
表示互为相反数的两个数的点,在数轴上分别位于原点的两侧,并且与原点的距离相等.
注意
例 3
例题讲解
画一条数轴,并标出表示下列各数的相反数的点:
3,1.5,-6.
解:3的相反数是-3;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如图所示.
1.代数意义:如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数.数a的相反数记作-a.特别地,0的相反数是0.
2.几何意义:表示互为相反数的两个点,在数轴上分别位于原点的两侧,并且与原点的距离相等.
3.-a表示a的相反数.因此,在这个数的前面添上“-”号,就得到这个数的相反数.正数的“+”号可省略不写,因此,在一个数前面添上“+”号,表示这个数本身.
4.正数的相反数是负数,负数的相反数是正数,0的相反数是0.
总结
补充练习
1.判断题,看谁回答的又对又快!
(1)-10是10的相反数. ( )
(2)10是10的相反数. ( )
(3)1.5与-1.5互为相反数.( )
(4)-2是相反数. ( )
×
√
√
×
2.(1)数轴上离原点3个单位长度的点所表示的数是________,它们的关系为____________.
(2)在数轴上,若点A和点B分别表示互为相反数的两个数,点A在点B的左侧,并且这两个数的距离是12.8,则A=______,B=______.
3或-3
互为相反数
-6.4
6.4
说一说
-(+1)= -(-1)=
因为-1的相反数是1,所以-(-1)=1.
因为+1的相反数是-1,所以-(+1)=-1.
例 4
例题讲解
填空:-(+0.8)= ;-(-3)= .
-0.8
3
注意:
+a的相反数是-a,记作-(+a)=-a;
-a的相反数是+a,记作-(-a)=+a.
这里a可表示正数,负数和0.
总结
2.对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.如果有奇数个“-”号,结果的符号就是“-”号;如果有偶数个“-”号,结果的符号就是“+”号.
1.在一个数前面加上“-”号表示这个数的相反数;在一个数前面加上“+”仍表示这个数,“+”号可省略.
补充练习
1、化简下列各数的符号:
(1)-(+3); (2)+(-1);
(3)+(+); (4)-[-(+3.5)];
(5)-{-[+(-)]}; (6)-[-(-a)].
解:(1)-(+3)=-3; (2)+(-1)=-1;
(3)+(+)=; (4)-[-(+3.5)]=3.5;
(5)-{-[+(-)]}=-; (6)-[-(-a)]=-a.
2.(1)若+5前面有2 022个负号,化简后结果是多少?
(2)若-5前面有2 023个负号,化简后结果是多少?你能总结出什么规律?
解:(1)若+5前面有2 022个负号,化简后结果是+5.
(2)若-5前面有2 023个负号,化简后结果+5.
总结规律:若一个数的前面有奇数个负号,则化简的结果等于它的相反数;若一个数的前面有偶数个负号,则化简的结果等于它本身.
课堂小结
1.相反数
(1)定义:只有符号不同的两个数互为相反数.
(2)代数意义:a的相反数是-a,0的相反数是0.
(3)几何意义:互为相反数的两个点到原点的距离相等.
2.多重符号的化简
(1)偶数个“-”号,结果为正数.
(2)奇数个“-”号,结果为负数.
同课章节目录
