1.2.3 绝对值 课件 (共15张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 1.2.3 绝对值 课件 (共15张PPT)初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 580.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 18:16:15 | ||
图片预览




文档简介
(共15张PPT)
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.3 绝对值
学习目标
1.理解绝对值的概念及其几何意义;(重点、难点)
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.(难点)
动脑筋
新课导入
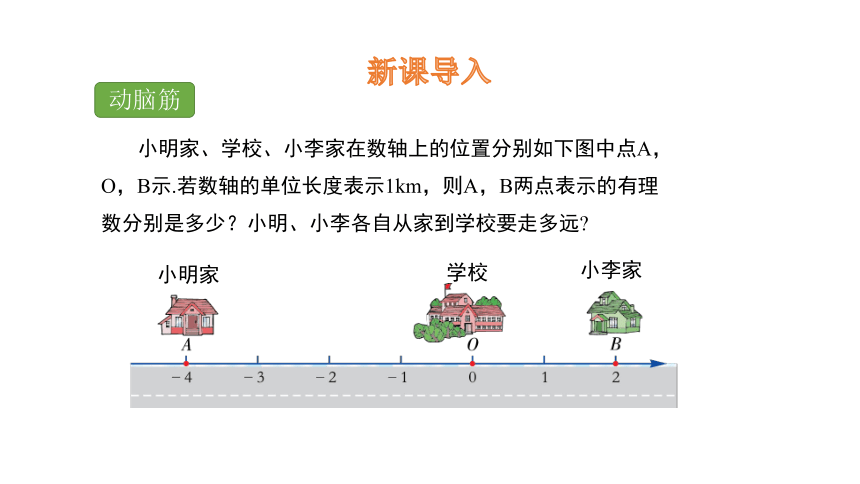
小明家、学校、小李家在数轴上的位置分别如下图中点A,O,B示.若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远
学校
小明家
小李家
点A表示-4,小明从家到学校要走4 km,点B表示2,小李从家到学校要走2 km.
学校
小明家
小李家
把4叫做-4的绝对值,记做“=4”.
把2叫做2的绝对值,记做“=2”.
从而,互为相反数的两个数的绝对值相等.
0的绝对值是0.
一般地,数学上规定:
正数的绝对值是它本身.
负数的绝对值是它的相反数.
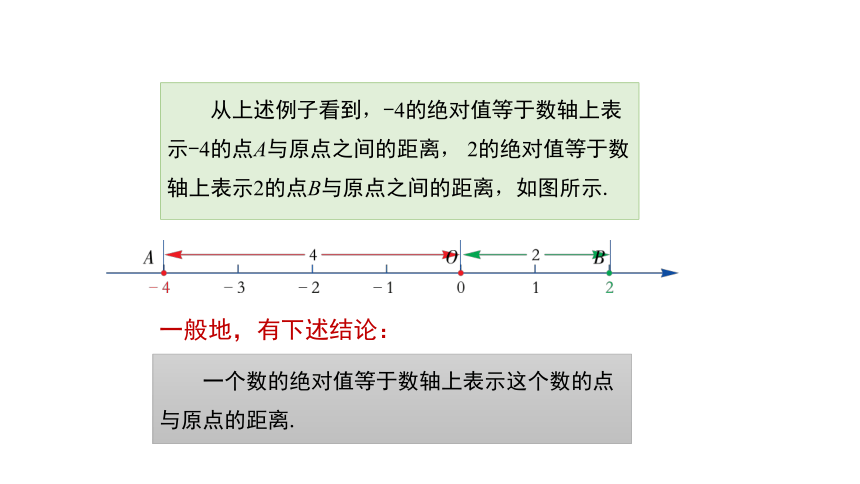
从上述例子看到,-4的绝对值等于数轴上表示-4的点A与原点之间的距离, 2的绝对值等于数轴上表示2的点B与原点之间的距离,如图所示.
一般地,有下述结论:
一个数的绝对值等于数轴上表示这个数的点与原点的距离.
例 5
例题讲解
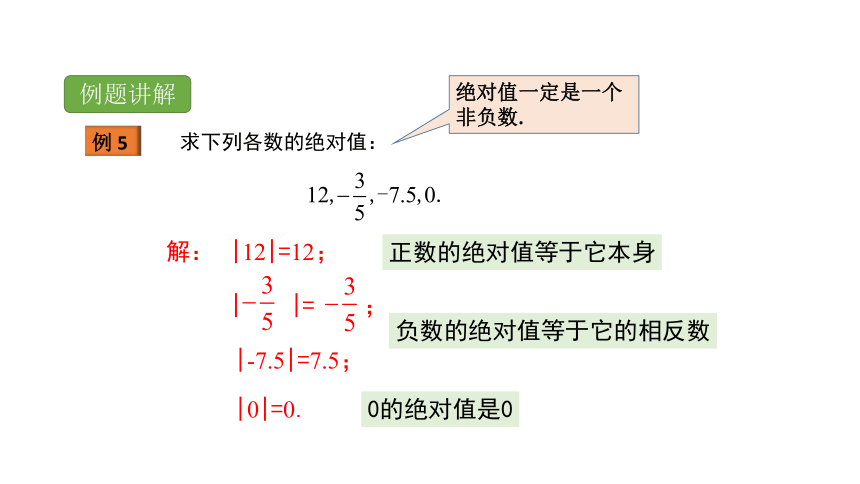
求下列各数的绝对值:
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
绝对值一定是一个
非负数.
补充练习
1.表示2.8的点与原点的距离是 个单位长度,即2.8的绝对值是 ,记作 ;
2.表示0的点与原点的距离是 个单位长度,即0的绝对值是 ,记作 ;
3. 表示-6的点与原点的距离是 个单位长度,即-6的绝对值是____,记作 .
2.8
2.8
|2.8|
0
0
|0|
6
6
|-6|
4.写出下列各数的绝对值:
解:
说一说
如果a表示一个数,则等于多少
一般地,如果a表示一个数,则
(1)当a是正数时,=a;
(2)当a=0时,=0;
(3)当a是负数时,=-a.
即是指a和-a中非负数的那一个数.
归纳
强调
若=8.7,求a.
解:因为绝对值等于8.7的有理数有8.7和-8.7两个,
所以a=8.7或a=-8.7.
例 6
例题讲解
互为相反数的两个数的绝对值相等.
补充练习
1.(1)绝对值是7的数有几个?各是什么?有没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7.
没有绝对值是-2的数.
(2)绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0.
(3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2.
2.已知|x|=2,|y|=3,且x解:因为|x|=2,|y|=3,
所以x=±2,y=±3.
又因为x所以x=2,y=3或x=-2,y=3.
解:根据题意可知x-4=0,y-3=0,
所以x=4,y=3,
故x+y=7.
【归纳】 几个非负数的和为0,则这几个数都为0.
3.已知=0,求x+y的值.
课堂小结
绝对值
定义
应用
几何意义
代数意义
求一个数的绝对值
用绝对值解决实际问题
由绝对值求数
|a|=a,(a>0)
|a|=-a,(a<0)
|a|=0,(a=0)
在数轴上,表示数a到原点的距离
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.3 绝对值
学习目标
1.理解绝对值的概念及其几何意义;(重点、难点)
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.(难点)
动脑筋
新课导入
小明家、学校、小李家在数轴上的位置分别如下图中点A,O,B示.若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远
学校
小明家
小李家
点A表示-4,小明从家到学校要走4 km,点B表示2,小李从家到学校要走2 km.
学校
小明家
小李家
把4叫做-4的绝对值,记做“=4”.
把2叫做2的绝对值,记做“=2”.
从而,互为相反数的两个数的绝对值相等.
0的绝对值是0.
一般地,数学上规定:
正数的绝对值是它本身.
负数的绝对值是它的相反数.
从上述例子看到,-4的绝对值等于数轴上表示-4的点A与原点之间的距离, 2的绝对值等于数轴上表示2的点B与原点之间的距离,如图所示.
一般地,有下述结论:
一个数的绝对值等于数轴上表示这个数的点与原点的距离.
例 5
例题讲解
求下列各数的绝对值:
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
绝对值一定是一个
非负数.
补充练习
1.表示2.8的点与原点的距离是 个单位长度,即2.8的绝对值是 ,记作 ;
2.表示0的点与原点的距离是 个单位长度,即0的绝对值是 ,记作 ;
3. 表示-6的点与原点的距离是 个单位长度,即-6的绝对值是____,记作 .
2.8
2.8
|2.8|
0
0
|0|
6
6
|-6|
4.写出下列各数的绝对值:
解:
说一说
如果a表示一个数,则等于多少
一般地,如果a表示一个数,则
(1)当a是正数时,=a;
(2)当a=0时,=0;
(3)当a是负数时,=-a.
即是指a和-a中非负数的那一个数.
归纳
强调
若=8.7,求a.
解:因为绝对值等于8.7的有理数有8.7和-8.7两个,
所以a=8.7或a=-8.7.
例 6
例题讲解
互为相反数的两个数的绝对值相等.
补充练习
1.(1)绝对值是7的数有几个?各是什么?有没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7.
没有绝对值是-2的数.
(2)绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0.
(3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2.
2.已知|x|=2,|y|=3,且x
所以x=±2,y=±3.
又因为x
解:根据题意可知x-4=0,y-3=0,
所以x=4,y=3,
故x+y=7.
【归纳】 几个非负数的和为0,则这几个数都为0.
3.已知=0,求x+y的值.
课堂小结
绝对值
定义
应用
几何意义
代数意义
求一个数的绝对值
用绝对值解决实际问题
由绝对值求数
|a|=a,(a>0)
|a|=-a,(a<0)
|a|=0,(a=0)
在数轴上,表示数a到原点的距离
同课章节目录
