1.2.1 数轴 课件(共16张PPT) 初中数学湘教版七年级上册
文档属性
| 名称 | 1.2.1 数轴 课件(共16张PPT) 初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 20:37:52 | ||
图片预览






文档简介
(共16张PPT)
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.1 数轴
学习目标
1.了解数轴的概念及其三个要素,会画数轴;(重点)
2.理解数轴上的点和有理数的对应关系.(难点)
我们看到的刻度尺的边缘上都有一些点,并且这些点在一条直线上,它们分别表示一些数.由此联想,能不能用一条直线上的点来表示数?
新课导入
观察
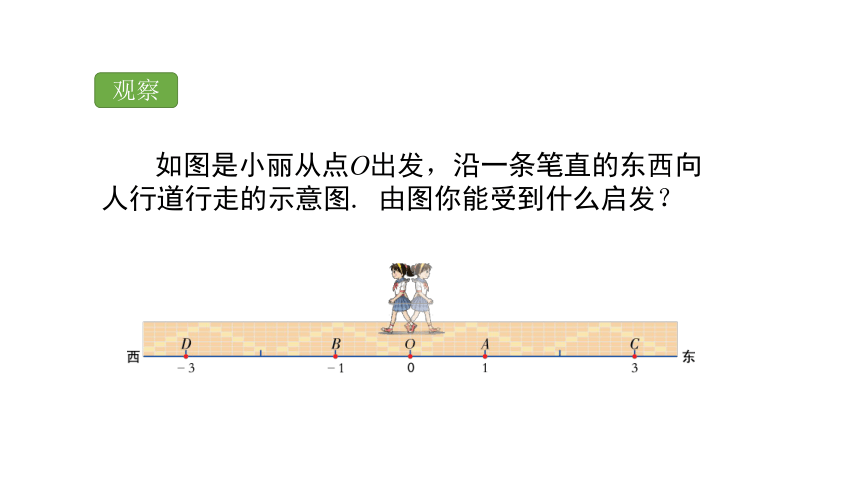
如图是小丽从点O出发,沿一条笔直的东西向人行道行走的示意图. 由图你能受到什么启发?
让出发点O表示0,向东走1m到达点A,就让点A表示1.向西走1m到达点B,就让点B表示-1.
向东走3m到达点C,就让点C表示3.向西走3m到达点D,就让点D表示-3.
从上面的例子受到启发,我们可以用一条直线上的点来直观地表示数.
画一条直线(通常把它水平放置),在直线上取一点O,把点O叫做原点,用原点表示0.
规定直线的正方向(标上箭头).通常把直线上从原点向右的方向规定为正方向,从原点向左的方向规定为负方向.
选取适当的长度为单位长度.
数轴的画法:
像这样,规定了原点、正方向和单位长度的直线叫做数轴.
归纳
1.数轴的三要素:原点、正方向和单位长度,三者
缺一不可.
2.任何有理数都可以用数轴上唯一的一个点来表示.
例题讲解
如下图,数轴上的点M,P,Q分别表示哪个有理数
解:点M,P,Q分别表示-3,-0.5,2.5.
例 1
画一条数轴,并标出表示下列各数的点:
-5, 1.5,-3.5, 4.5, ,.
解:所画数轴及各数在数轴上对应的点如下图所示.
例 2
注意:①把点标在线上;②把数标在点的上方,以便观看.
补充练习
1.关于数轴,下列说法中,最准确的是( )
A.一条直线
B.有原点、正方向的一条直线
C.有单位长度的一条直线
D.规定了原点、正方向、单位长度的直线
D
2.如图,数轴的单位长度为1,如果点A表示的数是-1,那么点B表示的数是( )
A.0 B.1
C.2 D.3
D
3.如图,在数轴上,若点B表示一个负数,则原点可以是( )
A.点E B.点D
C.点C D.点A
D
4.数轴上表示-2 的点在原点的_____侧,距原点的距离是______________;表示-6 的点在原点的____侧,距原点的距离是_____________;到表示 -2 的点的距离为 3 的点表示的数是________.
左
2 个单位长度
左
6 个单位长度
-5或1
方法总结:利用数轴可直观的求出两点的距离,由于距离没有方向性,所以到某点距离为某个正值的点一般有两个,因此要注意考虑所有情况.
5.下面所画数轴(如图)正确的是________(填序号).
①④
注意:在画数轴时常出现以下三种错误:
①“三要素”不全;
②单位长度不统一;
③标数时顺序不对.
课堂小结
数轴
应用
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
画法
一画:画直线
二定:定原点
三选:选正方向
四统一:统一单位长度
定义
规定了原点 、正方向 和 单位长度 的直线,叫做数轴.
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.1 数轴
学习目标
1.了解数轴的概念及其三个要素,会画数轴;(重点)
2.理解数轴上的点和有理数的对应关系.(难点)
我们看到的刻度尺的边缘上都有一些点,并且这些点在一条直线上,它们分别表示一些数.由此联想,能不能用一条直线上的点来表示数?
新课导入
观察
如图是小丽从点O出发,沿一条笔直的东西向人行道行走的示意图. 由图你能受到什么启发?
让出发点O表示0,向东走1m到达点A,就让点A表示1.向西走1m到达点B,就让点B表示-1.
向东走3m到达点C,就让点C表示3.向西走3m到达点D,就让点D表示-3.
从上面的例子受到启发,我们可以用一条直线上的点来直观地表示数.
画一条直线(通常把它水平放置),在直线上取一点O,把点O叫做原点,用原点表示0.
规定直线的正方向(标上箭头).通常把直线上从原点向右的方向规定为正方向,从原点向左的方向规定为负方向.
选取适当的长度为单位长度.
数轴的画法:
像这样,规定了原点、正方向和单位长度的直线叫做数轴.
归纳
1.数轴的三要素:原点、正方向和单位长度,三者
缺一不可.
2.任何有理数都可以用数轴上唯一的一个点来表示.
例题讲解
如下图,数轴上的点M,P,Q分别表示哪个有理数
解:点M,P,Q分别表示-3,-0.5,2.5.
例 1
画一条数轴,并标出表示下列各数的点:
-5, 1.5,-3.5, 4.5, ,.
解:所画数轴及各数在数轴上对应的点如下图所示.
例 2
注意:①把点标在线上;②把数标在点的上方,以便观看.
补充练习
1.关于数轴,下列说法中,最准确的是( )
A.一条直线
B.有原点、正方向的一条直线
C.有单位长度的一条直线
D.规定了原点、正方向、单位长度的直线
D
2.如图,数轴的单位长度为1,如果点A表示的数是-1,那么点B表示的数是( )
A.0 B.1
C.2 D.3
D
3.如图,在数轴上,若点B表示一个负数,则原点可以是( )
A.点E B.点D
C.点C D.点A
D
4.数轴上表示-2 的点在原点的_____侧,距原点的距离是______________;表示-6 的点在原点的____侧,距原点的距离是_____________;到表示 -2 的点的距离为 3 的点表示的数是________.
左
2 个单位长度
左
6 个单位长度
-5或1
方法总结:利用数轴可直观的求出两点的距离,由于距离没有方向性,所以到某点距离为某个正值的点一般有两个,因此要注意考虑所有情况.
5.下面所画数轴(如图)正确的是________(填序号).
①④
注意:在画数轴时常出现以下三种错误:
①“三要素”不全;
②单位长度不统一;
③标数时顺序不对.
课堂小结
数轴
应用
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
画法
一画:画直线
二定:定原点
三选:选正方向
四统一:统一单位长度
定义
规定了原点 、正方向 和 单位长度 的直线,叫做数轴.
同课章节目录
