2.5 第3课时 整式的加减 课件 (共16张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 2.5 第3课时 整式的加减 课件 (共16张PPT)初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 896.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 21:29:37 | ||
图片预览






文档简介
(共16张PPT)
第2章 代数式
2.5 整式的加法和减法
第3课时 整式的加减
学习目标
1.进一步经历用字母表示数量关系的过程,发展符号感.(重点)
2.灵活准确的运用整式的加减的步骤进行运算.(难点)
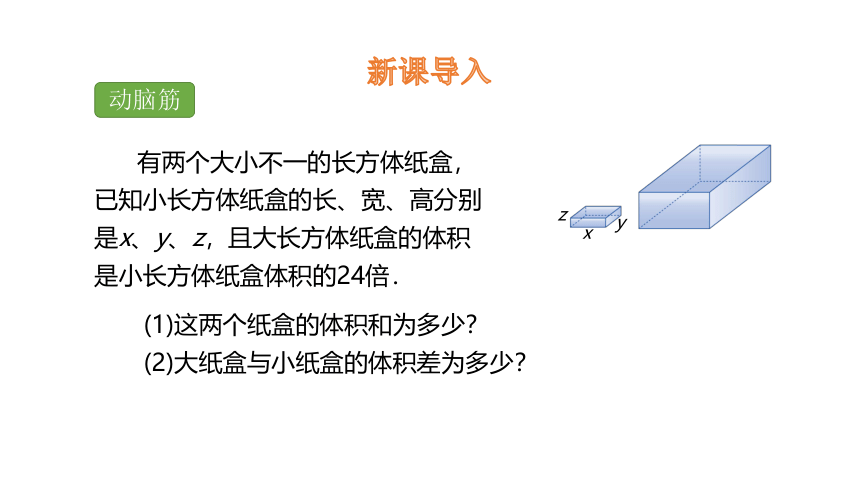
动脑筋
新课导入
有两个大小不一的长方体纸盒,已知小长方体纸盒的长、宽、高分别是x、y、z,且大长方体纸盒的体积是小长方体纸盒体积的24倍.
x
y
z
(1)这两个纸盒的体积和为多少?
(2)大纸盒与小纸盒的体积差为多少?
小纸盒和大纸盒的体积分别是xyz和24xyz,故两纸盒的体积和为xyz+24xyz=25xyz.
大纸盒的体积与小纸盒的体积差为24xyz-xyz=23xyz.
解:根据题意,得
求多项式 与多项式 的和与差.
去括号
合并同类项
例 4
例题讲解
例 5
先化简, 再求值.
5xy-(4x2 + 2xy)-2(2.5xy+10),其中x=1,y=-2.
解 5xy-(4x2+2xy)-2(2.5xy+10)
= 5xy-4x2-2xy-(5xy+20)
= 5xy-4x2-2xy-5xy-20
= -4x2-2xy-20.
当 x=1 ,y= -2 时,
-4x2-2xy-20= -4×12-2×1×(-2)-20= -20 .
例 6
如图,正方形的边长为x,用整式表示图中阴影部分的面积,并计算当x=4m时阴影部分的面积( 取3.14).
x
x
解:阴影部分的面积为
当x=4m 时,阴影部分的面积为
(1)整式的加减运算重点注意去括号时的符号、系数的处理,不要把符号弄错,不要漏乘括号外的系数;
(2)整式的化简求值题,能够化简的最好先化简,尽量不要直接把字母的值代入计算;
(3)解决整式加减的实际应用题时,先要把具体量用代数式表示出来,然后根据整式加减运算的法则、步骤进行计算;
(4)注意最后结果是几个单项式的和的形式,且要带单位时,要整体加括号.
归纳
整式化简求值的一般步骤
应用整式的加减进行化简求值,一般先去括号、合并同类项,再代入字母的值进行计算,简记为“一化二代三计算”,这样做能减少运算量,使计算简便.
补充练习
2.化简5(2x-3)+4(3-2x)的结果为( )
A.2x-3 B.2x+9 C.8x-3 D.18x-3
1.多项式3a-a2与单项式2a2的和等于( )
A.3a B.3a+a2 C.3a+2a2 D.4a2
B
A
3.加上5x2-3x-5等于3x的代数式是( )
A.-5x2+6x+5 B.5-5x2
C.5x2-6x-5 D.5x2-5
A
4.计算:
(1)7(p +p -p-1)-2(p +p);
7(p +p -p-1)-2(p +p)
=7p +7p -7p-7-2p -2p
=5p +7p -9p-7.
解:
5.求整式 与 的和.
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
6.已知|x|=2y,y=,且xy<0,
求代数式4(2x y-xy )-2(2xy +3x y)的值.
7.笔记本的单价是x元,圆珠笔的单价是y元.
小红买3本笔记本,2支圆珠笔;
小明买4本笔记本,3支圆珠笔.
买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红花费:(3x+2y)元;
小明花费:(4x+3y)元;
小红和小明一共花费:(3x+2y)+(4x+3y)=(7x+5y)元.
8.已知 A=3x +y -2xy,B=xy-y +2x .
求:(1)2A-3B;
(2)若|x+2|+(y-3) =0,求2A-3B的值.
解:(1)因为A=3x +y -2xy,B=xy-y +2x ,
所以2A-3B=2(3x +y -2xy)-3(xy-y +2x )=6x +2y -4xy-3xy+3y -6x =5y -7xy.
(2)因为|x+2|+(y-3) =0,
所以x+2=0,y-3=0,所以x=-2,y=3.
当x=-2,y=3时,2A-3B=5y -7xy=5×(-2) -7×(-2)×3=62.
课堂小结
②合并同类项
①去括号
再代入求值
整式的加减
先化简
整式加减的步骤
整式的化简求值
第2章 代数式
2.5 整式的加法和减法
第3课时 整式的加减
学习目标
1.进一步经历用字母表示数量关系的过程,发展符号感.(重点)
2.灵活准确的运用整式的加减的步骤进行运算.(难点)
动脑筋
新课导入
有两个大小不一的长方体纸盒,已知小长方体纸盒的长、宽、高分别是x、y、z,且大长方体纸盒的体积是小长方体纸盒体积的24倍.
x
y
z
(1)这两个纸盒的体积和为多少?
(2)大纸盒与小纸盒的体积差为多少?
小纸盒和大纸盒的体积分别是xyz和24xyz,故两纸盒的体积和为xyz+24xyz=25xyz.
大纸盒的体积与小纸盒的体积差为24xyz-xyz=23xyz.
解:根据题意,得
求多项式 与多项式 的和与差.
去括号
合并同类项
例 4
例题讲解
例 5
先化简, 再求值.
5xy-(4x2 + 2xy)-2(2.5xy+10),其中x=1,y=-2.
解 5xy-(4x2+2xy)-2(2.5xy+10)
= 5xy-4x2-2xy-(5xy+20)
= 5xy-4x2-2xy-5xy-20
= -4x2-2xy-20.
当 x=1 ,y= -2 时,
-4x2-2xy-20= -4×12-2×1×(-2)-20= -20 .
例 6
如图,正方形的边长为x,用整式表示图中阴影部分的面积,并计算当x=4m时阴影部分的面积( 取3.14).
x
x
解:阴影部分的面积为
当x=4m 时,阴影部分的面积为
(1)整式的加减运算重点注意去括号时的符号、系数的处理,不要把符号弄错,不要漏乘括号外的系数;
(2)整式的化简求值题,能够化简的最好先化简,尽量不要直接把字母的值代入计算;
(3)解决整式加减的实际应用题时,先要把具体量用代数式表示出来,然后根据整式加减运算的法则、步骤进行计算;
(4)注意最后结果是几个单项式的和的形式,且要带单位时,要整体加括号.
归纳
整式化简求值的一般步骤
应用整式的加减进行化简求值,一般先去括号、合并同类项,再代入字母的值进行计算,简记为“一化二代三计算”,这样做能减少运算量,使计算简便.
补充练习
2.化简5(2x-3)+4(3-2x)的结果为( )
A.2x-3 B.2x+9 C.8x-3 D.18x-3
1.多项式3a-a2与单项式2a2的和等于( )
A.3a B.3a+a2 C.3a+2a2 D.4a2
B
A
3.加上5x2-3x-5等于3x的代数式是( )
A.-5x2+6x+5 B.5-5x2
C.5x2-6x-5 D.5x2-5
A
4.计算:
(1)7(p +p -p-1)-2(p +p);
7(p +p -p-1)-2(p +p)
=7p +7p -7p-7-2p -2p
=5p +7p -9p-7.
解:
5.求整式 与 的和.
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
6.已知|x|=2y,y=,且xy<0,
求代数式4(2x y-xy )-2(2xy +3x y)的值.
7.笔记本的单价是x元,圆珠笔的单价是y元.
小红买3本笔记本,2支圆珠笔;
小明买4本笔记本,3支圆珠笔.
买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红花费:(3x+2y)元;
小明花费:(4x+3y)元;
小红和小明一共花费:(3x+2y)+(4x+3y)=(7x+5y)元.
8.已知 A=3x +y -2xy,B=xy-y +2x .
求:(1)2A-3B;
(2)若|x+2|+(y-3) =0,求2A-3B的值.
解:(1)因为A=3x +y -2xy,B=xy-y +2x ,
所以2A-3B=2(3x +y -2xy)-3(xy-y +2x )=6x +2y -4xy-3xy+3y -6x =5y -7xy.
(2)因为|x+2|+(y-3) =0,
所以x+2=0,y-3=0,所以x=-2,y=3.
当x=-2,y=3时,2A-3B=5y -7xy=5×(-2) -7×(-2)×3=62.
课堂小结
②合并同类项
①去括号
再代入求值
整式的加减
先化简
整式加减的步骤
整式的化简求值
同课章节目录
