3.1 建立一元一次方程模型 课件 (共19张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 3.1 建立一元一次方程模型 课件 (共19张PPT)初中数学湘教版七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 626.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 21:30:07 | ||
图片预览






文档简介
(共19张PPT)
第3章 一元一次方程
3.1 建立一元一次方程模型
学习目标
1. 理解方程、一元一次方程及方程的解的概念.
2. 会根据具体问题中的等量关系列出一元一次方程.(重点、难点)
动脑筋
新课导入
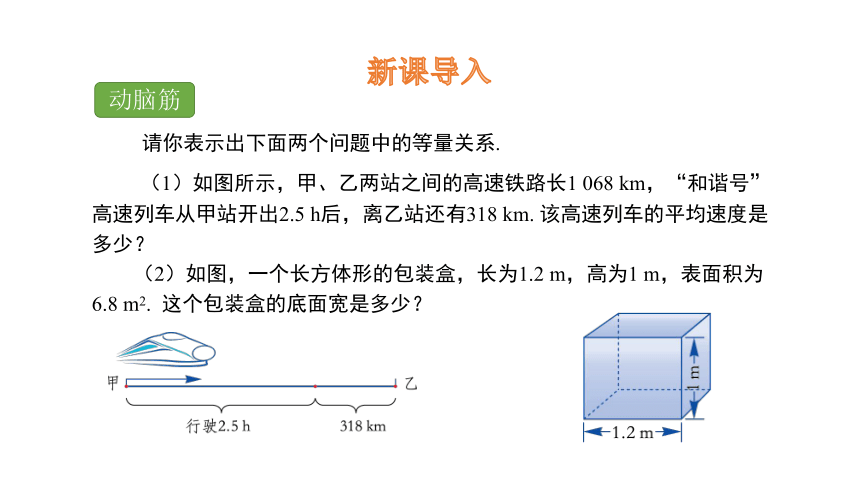
请你表示出下面两个问题中的等量关系.
(1)如图所示,甲、乙两站之间的高速铁路长1 068 km,“和谐号”高速列车从甲站开出2.5 h后,离乙站还有318 km. 该高速列车的平均速度是多少?
(2)如图,一个长方体形的包装盒,长为1.2 m,高为1 m,表面积为6.8 m2. 这个包装盒的底面宽是多少?
对于(1),如果设高速列车的平均速度为x km/h,我们可以用含x的式子表示上述等量关系,即
2.5x + 318 = 1 068
问题(1)的等量关系是:
已行驶的路程+剩余的路程=全长.
对于(2),若设包装盒的底面宽是y m,则等量关系可表示为
1.2×y×2+y×1×2+1.2×1×2 = 6.8,
即
2.4y + 2y + 2.4= 6.8
问题(2)的等量关系是:底面积+侧面积=表面积.
在等式2.5x +318=1 068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程.
归纳
2.5x + 318 = 1 068
已知数
未知数
2.5x + 318 = 1 068,
2.4y + 2y + 2.4= 6.8,
x – 2y = 6,
如
这些等式都是方程.
中,x,y,t 都是未知数,
像上面这样,把所要求的量用字母x(或y,…)表示,根据问题中的等量关系列出方程,这一过程叫做建立方程.
方程2.5x + 318 = 1 068、 2.4y + 2y + 2.4= 6.8中,每个方程含有几个未知数?每个未知数的次数是多少?
说一说
像2.5x + 318 = 1 068, 2.4y + 2y + 2.4= 6.8这样,只含有一个未知数,并且未知数的次数是1,我们把这样的方程叫做一元一次方程.
2.5x + 318 = 1 068有一个未知数,次数是1.
2.4y + 2y + 2.4= 6.8有一个未知数,次数是1.
(2)方程中只有一个未知数;
(3)未知数的次数是1.
判断一个方程是一元一次方程,化简后必须满足三个条件:
(1)等号两边都是整式;
归纳
判断下列各式是不是一元一次方程.
①2x2-5=4;②-m+8=1;③x=1;④x+y=1;
⑤x+3>0;⑥2x2-2(x2-x)=1;⑦ ;⑧πx=12.
解:①未知数的指数是1,所以不是;④含有2个未知数,所以不是;
⑤不是等式,所以不是;⑦未知数指数不是1,所以不是.
注意:⑥2x -2(x -x)=1,可化简为2x=1,所以⑥是一元一次方程.
补充练习
√
√
√
√
能使方程左、右两边相等的未知数的值.叫做方程的解.
在方程x+5=8中,当x=3时,方程两边的值相等,我们就说x=3是方程x+5=8的解.
例
例题讲解
检验下列x的值是否是方程2.5x+318=1 068的解.
(1)x=300; (2)x=330.
解:(1)把x=300代入原方程得,
左边=2.5×300+318=1 068,
左边=右边,
所以x=300是方程2.5x+318=1 068的解.
例
例题讲解
检验下列x的值是否是方程2.5x+318=1 068的解.
(1)x=300; (2)x=330.
(2)把x=330代入原方程得,
左边=2.5×330+318=1 143,
左边≠右边,
所以x=330不是方程2.5x+318=1 068的解.
判断方程解的三个步骤:
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号的左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.
总结
补充练习
1.已知九年级某班30名学生种树72棵,男生每人种3棵树,女生每人种2棵树,设男生有x人,则下面所列方程正确的是( )
A.2x+3(72-x)=30 B.3x+2(72-x)=30
C.2x+3(30-x)=72 D.3x+2(30-x)=72
2. 根据下列条件能列出方程的是( )
A.a与5的和的3倍 B.甲数的3倍与乙数的2倍的和
C.a与b的差的15% D.一个数的5倍是18
D
D
3.已知关于 x 的一元一次方程2(x-1)+3a=3的解为4,则 a 的值是( )
A.-1 B.1 C.-2 D.-3
解析:将x=4代入2(x-1)+3a=3,得2×3+3a=3,解得a= -1.
A
技巧点拨:根据方程的解的定义求有关字母的值时,通常先将解代入方程中,得到关于字母的方程,求解即可得到这个字母的值.
4.下列方程是一元一次方程的是( )
A.-2=0 B.2x=1 C.x+2y=5 D.x2-1=2x
B
5.x=5是下列方程的解吗?
(1)2x+(15-x)=10;
(2)4x -12x+5=9x.
不是
是
6.(分类讨论题)若方程3-3x +2x-2=0是关于x的一元一次方程,求n -n+1的值.
课堂小结
建立一元一次方程模型
方程的有关概念
一元一次方程的概念
建立一元一次方程模型
设字母表示数
把其他部分的量也用字母表示出来
找等量关系,列出方程
方程的概念
方程的解概念
第3章 一元一次方程
3.1 建立一元一次方程模型
学习目标
1. 理解方程、一元一次方程及方程的解的概念.
2. 会根据具体问题中的等量关系列出一元一次方程.(重点、难点)
动脑筋
新课导入
请你表示出下面两个问题中的等量关系.
(1)如图所示,甲、乙两站之间的高速铁路长1 068 km,“和谐号”高速列车从甲站开出2.5 h后,离乙站还有318 km. 该高速列车的平均速度是多少?
(2)如图,一个长方体形的包装盒,长为1.2 m,高为1 m,表面积为6.8 m2. 这个包装盒的底面宽是多少?
对于(1),如果设高速列车的平均速度为x km/h,我们可以用含x的式子表示上述等量关系,即
2.5x + 318 = 1 068
问题(1)的等量关系是:
已行驶的路程+剩余的路程=全长.
对于(2),若设包装盒的底面宽是y m,则等量关系可表示为
1.2×y×2+y×1×2+1.2×1×2 = 6.8,
即
2.4y + 2y + 2.4= 6.8
问题(2)的等量关系是:底面积+侧面积=表面积.
在等式2.5x +318=1 068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程.
归纳
2.5x + 318 = 1 068
已知数
未知数
2.5x + 318 = 1 068,
2.4y + 2y + 2.4= 6.8,
x – 2y = 6,
如
这些等式都是方程.
中,x,y,t 都是未知数,
像上面这样,把所要求的量用字母x(或y,…)表示,根据问题中的等量关系列出方程,这一过程叫做建立方程.
方程2.5x + 318 = 1 068、 2.4y + 2y + 2.4= 6.8中,每个方程含有几个未知数?每个未知数的次数是多少?
说一说
像2.5x + 318 = 1 068, 2.4y + 2y + 2.4= 6.8这样,只含有一个未知数,并且未知数的次数是1,我们把这样的方程叫做一元一次方程.
2.5x + 318 = 1 068有一个未知数,次数是1.
2.4y + 2y + 2.4= 6.8有一个未知数,次数是1.
(2)方程中只有一个未知数;
(3)未知数的次数是1.
判断一个方程是一元一次方程,化简后必须满足三个条件:
(1)等号两边都是整式;
归纳
判断下列各式是不是一元一次方程.
①2x2-5=4;②-m+8=1;③x=1;④x+y=1;
⑤x+3>0;⑥2x2-2(x2-x)=1;⑦ ;⑧πx=12.
解:①未知数的指数是1,所以不是;④含有2个未知数,所以不是;
⑤不是等式,所以不是;⑦未知数指数不是1,所以不是.
注意:⑥2x -2(x -x)=1,可化简为2x=1,所以⑥是一元一次方程.
补充练习
√
√
√
√
能使方程左、右两边相等的未知数的值.叫做方程的解.
在方程x+5=8中,当x=3时,方程两边的值相等,我们就说x=3是方程x+5=8的解.
例
例题讲解
检验下列x的值是否是方程2.5x+318=1 068的解.
(1)x=300; (2)x=330.
解:(1)把x=300代入原方程得,
左边=2.5×300+318=1 068,
左边=右边,
所以x=300是方程2.5x+318=1 068的解.
例
例题讲解
检验下列x的值是否是方程2.5x+318=1 068的解.
(1)x=300; (2)x=330.
(2)把x=330代入原方程得,
左边=2.5×330+318=1 143,
左边≠右边,
所以x=330不是方程2.5x+318=1 068的解.
判断方程解的三个步骤:
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号的左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.
总结
补充练习
1.已知九年级某班30名学生种树72棵,男生每人种3棵树,女生每人种2棵树,设男生有x人,则下面所列方程正确的是( )
A.2x+3(72-x)=30 B.3x+2(72-x)=30
C.2x+3(30-x)=72 D.3x+2(30-x)=72
2. 根据下列条件能列出方程的是( )
A.a与5的和的3倍 B.甲数的3倍与乙数的2倍的和
C.a与b的差的15% D.一个数的5倍是18
D
D
3.已知关于 x 的一元一次方程2(x-1)+3a=3的解为4,则 a 的值是( )
A.-1 B.1 C.-2 D.-3
解析:将x=4代入2(x-1)+3a=3,得2×3+3a=3,解得a= -1.
A
技巧点拨:根据方程的解的定义求有关字母的值时,通常先将解代入方程中,得到关于字母的方程,求解即可得到这个字母的值.
4.下列方程是一元一次方程的是( )
A.-2=0 B.2x=1 C.x+2y=5 D.x2-1=2x
B
5.x=5是下列方程的解吗?
(1)2x+(15-x)=10;
(2)4x -12x+5=9x.
不是
是
6.(分类讨论题)若方程3-3x +2x-2=0是关于x的一元一次方程,求n -n+1的值.
课堂小结
建立一元一次方程模型
方程的有关概念
一元一次方程的概念
建立一元一次方程模型
设字母表示数
把其他部分的量也用字母表示出来
找等量关系,列出方程
方程的概念
方程的解概念
同课章节目录
