1.6 有理数的乘方 课件(共30张PPT) 初中数学湘教版七年级上册
文档属性
| 名称 | 1.6 有理数的乘方 课件(共30张PPT) 初中数学湘教版七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 21:31:30 | ||
图片预览








文档简介
(共30张PPT)
第1章 有理数
1.6 有理数的乘方
第1课时 有理数的乘方
学习目标
1.理解并掌握有理数的乘方、幂、底数、指数的概
念及意义.(重点)
2.能够正确进行有理数的乘方运算.(难点)
动脑筋
新课导入
(-2)×(-2)×(-2)×(-2)×(-2)可以简记为什么?
在小学我们就学过,2×2可以简记为22,2×2×2可以简记为23. 类似地,我们把(-2)×(-2)×(-2)×(-2)×(-2)简记为(-2)5.
一般地,a 是有理数,n 是正整数,则把
a × a × a ×…×a 简记为 an,
n 个
我们把 an 读作 a 的 n 次方,也读做 a 的 n 次幂.
即
an = a × a × a ×…×a
n 个
知识要点
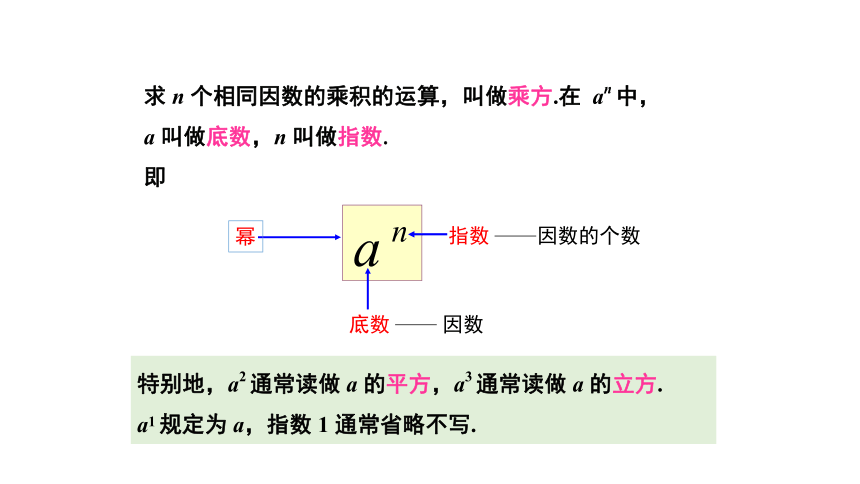
求 n 个相同因数的乘积的运算,叫做乘方.在 an 中, a 叫做底数,n 叫做指数.
即
幂
指数
因数的个数
底数
因数
特别地,a2 通常读做 a 的平方,a3 通常读做 a 的立方.
a1 规定为 a,指数 1 通常省略不写.
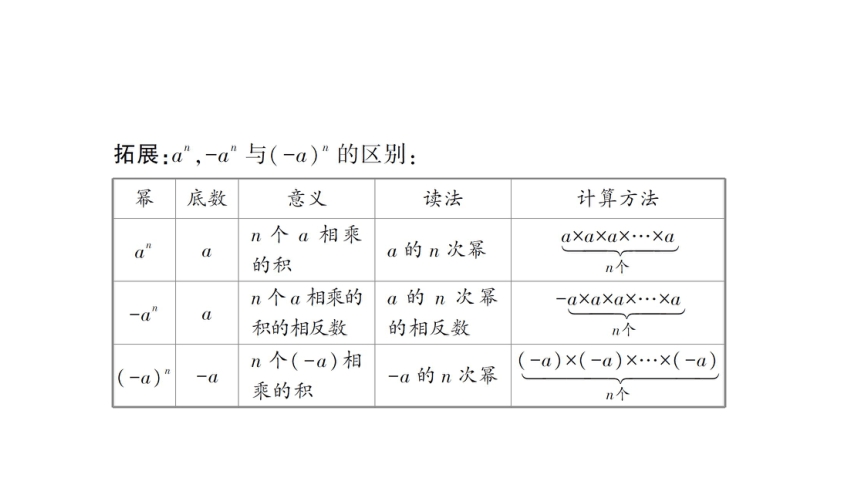
(-2)4 与 -24 的含义相同吗?它们的结果相同吗?(-2)3 与 -23 的含义与结果也分别相同吗?
(-2)3 表示 -2 的 3 次方. -23 表示 2 的 3 次方的相反数.
议一议
(-2)4与表示-2的4次方.
-24 表示2的4次方的相反数.
......
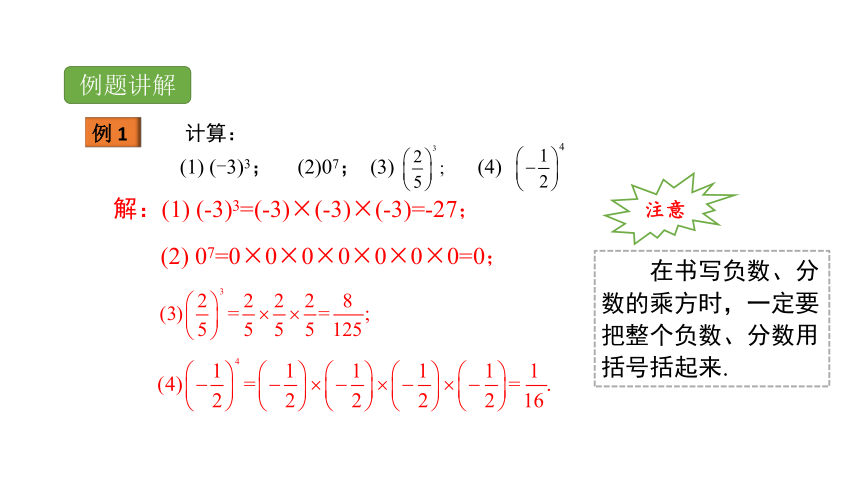
例 1
例题讲解
计算:
(1) (-3)3; (2)07; (3) (4)
解:(1) (-3)3=(-3)×(-3)×(-3)=-27;
(2) 07=0×0×0×0×0×0×0=0;
在书写负数、分数的乘方时,一定要把整个负数、分数用括号括起来.
注意
补充练习
完成下面的内容,寻找规律:
(1)22=___,23= ___ ,24= ___ ,25= ___;
(2)(-2)2= ___ ,(-2)3= ___ ,
(-2)4= ___,(-2)5= _____ ;
(3)(-1)1= ___ ,(-1)3= ___ ,
(-1)4= ___ ,(-1)5= ___ ;
(4)02= ___ ,03= ___ ,
04= ___ ,05= ___ .
32
4
4
8
16
-8
16
-32
1
1
-1
-1
0
0
0
0
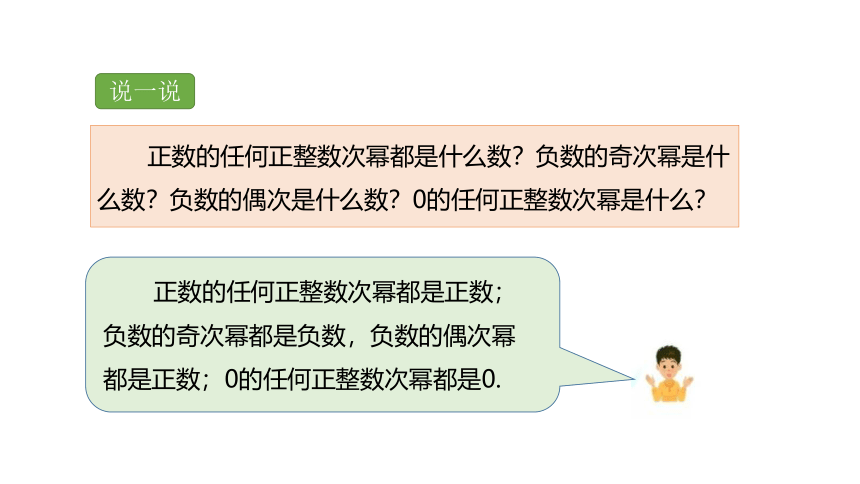
正数的任何正整数次幂都是什么数?负数的奇次幂是什么数?负数的偶次是什么数?0的任何正整数次幂是什么?
正数的任何正整数次幂都是正数;负数的奇次幂都是负数,负数的偶次幂都是正数;0的任何正整数次幂都是0.
说一说
知识要点
有理数乘方运算的符号法则
正数的任何正整数次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0 的任何正整数次幂都是 0.
有理数乘方运算的步骤
将有理数的乘方运算转化为乘法运算,先确定幂的符号,再计算幂的绝对值.
例 2
例题讲解
总结:先乘方,再乘除;如果有括号,先进行括号里的运算.
计算:
解:
1.填空:
(1) -(-3)2 = ; (2) -32 = ;
(3) (-5)3 = ; (4) 0.13 = ;
(5) (-1)9 = ; (6) (-1)12 = ;
(7) (-1)n = .
-9
-9
-125
0.001
-1
1
(当 n 为正奇数时)
(当 n 为正偶数时)
补充练习
2.计算:
(1) ; (2)-23×(-32)
(3)64÷(-2)5 ; (4)(-4)3÷(-1)200 + 2×(-3)4
(2)-23×(-32) = -8×(-9) = 72;
(3)64÷(-2)5 = 64÷(-32) = -2;
(4)(-4)3÷(-1)200 + 2×(-3)4 = -64÷1 + 2×81 = 98.
方法总结:几个非负数的和为 0,则这几个数都等于 0.
3.如果 |x-3| +(y+2)2=0,求 yx 的值.
且 |x-3| +(y+2)2=0,
解:∵ |x-3| ≥0,(y+2)2≥0
∴ |x-3| =0,(y+2)2=0,
∴x=3,y=-2,
∴yx=(-2)3=-8.
4.计算:0.1252 023×82 024.
2 024 个
2 023 个
2 023 个
解:原式 =
课堂小结
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正数次幂都是零.
幂
指数
因数的个数
底数
因数
第1章 有理数
1.6 有理数的乘方
第2课时 科学记数法
学习目标
1.能用科学记数法表示大数,会把用科学记数法表示的大数还原成原数.(重点)
2.归纳出科学记数法中指数与整数位数之间的关系.(难点)
新课导入
在日常生活中,我们会遇到一些较大的数,如地球的表面积约为 511 000 000 km2,能不能用一种较简单的方式来表示这样的大数?
5.11×108
102,103,104,… ,10n分别等于多少?你发现了什么?
探究
,,
,…,
10的n次幂就是1后面有n个0
我们可以利用10的乘方来表示一些大数,例如,
511 000 000=5.11×100 000 000=5.11×,
读做5.11乘10的8次方.
把一个绝对值大于10的数表记做a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10,n是整数),这种记数法叫科学记数法.
科学记数法的形式为a×10n ,其中n为正整数.
210 000 000 = 2.1×108
8 + 1 位
科学记数法中 10 的指数 n 值的确定法:
①比原整数位数少 1 (当原数的绝对值≥10 时);
②由小数点的移动位数来确定.
指数为 8
反之,1后面有多少个0,10的幂指数就是多少.
例 3
例题讲解
用科学记数法表示下列各数:
(1)108 000 000; (2)-32 000 000.
解 (1)108 000 000=1.08× ;
(2)-32 000 000=-3.2× .
2010年11月14日,半年评选一次的全球超级计算机500强名单正式公布,我国“天河一号”超级计算机以每秒 2 570 万亿次的实测运算速度,成为世界运算最快的超级计算机.请用科学记数法表示“天河一号”的实测运算速度为每秒多少次.
解: 2 570万亿就是2 570 000 000 000 000.
用科学记数法表示为2.57 × 1015,即“天河一号”的实测运算速度为每秒2.57 × 1015次.
补充练习
1.节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约 3 亿 5 千万人.3 亿 5 千万用科学记数法表示为( )
A.3.5×107 B.3.5×108
C.3.5×109 D.3.5×1010
B
2. 将下列用科学记数法表示的数还原成原数:
(1)1.23×107
(2)-3.141 592×105
解:(1)1.23×107 = 12 300 000;
(2)-3.141 592×105 = -314 159.2.
3. 用科学记数法表示下列各数:
(1)181 万;
(2)612 亿;
(3)1230.5 万;
(4)398.2 千万.
3. 用科学记数法表示下列各数:
(1)181 万;
(2)612 亿;
(3)1230.5 万;
(4)398.2 千万.
解:(1)181 万 = 1 810 000=1.81×106;
(2)612 亿=61 200 000 000=6.12×1010;
(3)1230.5 万=12 305 000=1.230 5×107;
(4)398.2 千万=3 982 000 000=3.982×109.
一个绝对值大于 10 的数都可记成 a×10n 的形式,其中 a 的取值范围 1≤a<10 .n 等于原数整数位减 1.这种记数方法叫做科学记数法.
科学记数法
概念
应用
表示绝对值大于 10 的数
根据科学记数法写原数
n 等于整数位数减 1
原数整数位数等于指数 n 加 1
课堂小结
第1章 有理数
1.6 有理数的乘方
第1课时 有理数的乘方
学习目标
1.理解并掌握有理数的乘方、幂、底数、指数的概
念及意义.(重点)
2.能够正确进行有理数的乘方运算.(难点)
动脑筋
新课导入
(-2)×(-2)×(-2)×(-2)×(-2)可以简记为什么?
在小学我们就学过,2×2可以简记为22,2×2×2可以简记为23. 类似地,我们把(-2)×(-2)×(-2)×(-2)×(-2)简记为(-2)5.
一般地,a 是有理数,n 是正整数,则把
a × a × a ×…×a 简记为 an,
n 个
我们把 an 读作 a 的 n 次方,也读做 a 的 n 次幂.
即
an = a × a × a ×…×a
n 个
知识要点
求 n 个相同因数的乘积的运算,叫做乘方.在 an 中, a 叫做底数,n 叫做指数.
即
幂
指数
因数的个数
底数
因数
特别地,a2 通常读做 a 的平方,a3 通常读做 a 的立方.
a1 规定为 a,指数 1 通常省略不写.
(-2)4 与 -24 的含义相同吗?它们的结果相同吗?(-2)3 与 -23 的含义与结果也分别相同吗?
(-2)3 表示 -2 的 3 次方. -23 表示 2 的 3 次方的相反数.
议一议
(-2)4与表示-2的4次方.
-24 表示2的4次方的相反数.
......
例 1
例题讲解
计算:
(1) (-3)3; (2)07; (3) (4)
解:(1) (-3)3=(-3)×(-3)×(-3)=-27;
(2) 07=0×0×0×0×0×0×0=0;
在书写负数、分数的乘方时,一定要把整个负数、分数用括号括起来.
注意
补充练习
完成下面的内容,寻找规律:
(1)22=___,23= ___ ,24= ___ ,25= ___;
(2)(-2)2= ___ ,(-2)3= ___ ,
(-2)4= ___,(-2)5= _____ ;
(3)(-1)1= ___ ,(-1)3= ___ ,
(-1)4= ___ ,(-1)5= ___ ;
(4)02= ___ ,03= ___ ,
04= ___ ,05= ___ .
32
4
4
8
16
-8
16
-32
1
1
-1
-1
0
0
0
0
正数的任何正整数次幂都是什么数?负数的奇次幂是什么数?负数的偶次是什么数?0的任何正整数次幂是什么?
正数的任何正整数次幂都是正数;负数的奇次幂都是负数,负数的偶次幂都是正数;0的任何正整数次幂都是0.
说一说
知识要点
有理数乘方运算的符号法则
正数的任何正整数次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0 的任何正整数次幂都是 0.
有理数乘方运算的步骤
将有理数的乘方运算转化为乘法运算,先确定幂的符号,再计算幂的绝对值.
例 2
例题讲解
总结:先乘方,再乘除;如果有括号,先进行括号里的运算.
计算:
解:
1.填空:
(1) -(-3)2 = ; (2) -32 = ;
(3) (-5)3 = ; (4) 0.13 = ;
(5) (-1)9 = ; (6) (-1)12 = ;
(7) (-1)n = .
-9
-9
-125
0.001
-1
1
(当 n 为正奇数时)
(当 n 为正偶数时)
补充练习
2.计算:
(1) ; (2)-23×(-32)
(3)64÷(-2)5 ; (4)(-4)3÷(-1)200 + 2×(-3)4
(2)-23×(-32) = -8×(-9) = 72;
(3)64÷(-2)5 = 64÷(-32) = -2;
(4)(-4)3÷(-1)200 + 2×(-3)4 = -64÷1 + 2×81 = 98.
方法总结:几个非负数的和为 0,则这几个数都等于 0.
3.如果 |x-3| +(y+2)2=0,求 yx 的值.
且 |x-3| +(y+2)2=0,
解:∵ |x-3| ≥0,(y+2)2≥0
∴ |x-3| =0,(y+2)2=0,
∴x=3,y=-2,
∴yx=(-2)3=-8.
4.计算:0.1252 023×82 024.
2 024 个
2 023 个
2 023 个
解:原式 =
课堂小结
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正数次幂都是零.
幂
指数
因数的个数
底数
因数
第1章 有理数
1.6 有理数的乘方
第2课时 科学记数法
学习目标
1.能用科学记数法表示大数,会把用科学记数法表示的大数还原成原数.(重点)
2.归纳出科学记数法中指数与整数位数之间的关系.(难点)
新课导入
在日常生活中,我们会遇到一些较大的数,如地球的表面积约为 511 000 000 km2,能不能用一种较简单的方式来表示这样的大数?
5.11×108
102,103,104,… ,10n分别等于多少?你发现了什么?
探究
,,
,…,
10的n次幂就是1后面有n个0
我们可以利用10的乘方来表示一些大数,例如,
511 000 000=5.11×100 000 000=5.11×,
读做5.11乘10的8次方.
把一个绝对值大于10的数表记做a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10,n是整数),这种记数法叫科学记数法.
科学记数法的形式为a×10n ,其中n为正整数.
210 000 000 = 2.1×108
8 + 1 位
科学记数法中 10 的指数 n 值的确定法:
①比原整数位数少 1 (当原数的绝对值≥10 时);
②由小数点的移动位数来确定.
指数为 8
反之,1后面有多少个0,10的幂指数就是多少.
例 3
例题讲解
用科学记数法表示下列各数:
(1)108 000 000; (2)-32 000 000.
解 (1)108 000 000=1.08× ;
(2)-32 000 000=-3.2× .
2010年11月14日,半年评选一次的全球超级计算机500强名单正式公布,我国“天河一号”超级计算机以每秒 2 570 万亿次的实测运算速度,成为世界运算最快的超级计算机.请用科学记数法表示“天河一号”的实测运算速度为每秒多少次.
解: 2 570万亿就是2 570 000 000 000 000.
用科学记数法表示为2.57 × 1015,即“天河一号”的实测运算速度为每秒2.57 × 1015次.
补充练习
1.节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约 3 亿 5 千万人.3 亿 5 千万用科学记数法表示为( )
A.3.5×107 B.3.5×108
C.3.5×109 D.3.5×1010
B
2. 将下列用科学记数法表示的数还原成原数:
(1)1.23×107
(2)-3.141 592×105
解:(1)1.23×107 = 12 300 000;
(2)-3.141 592×105 = -314 159.2.
3. 用科学记数法表示下列各数:
(1)181 万;
(2)612 亿;
(3)1230.5 万;
(4)398.2 千万.
3. 用科学记数法表示下列各数:
(1)181 万;
(2)612 亿;
(3)1230.5 万;
(4)398.2 千万.
解:(1)181 万 = 1 810 000=1.81×106;
(2)612 亿=61 200 000 000=6.12×1010;
(3)1230.5 万=12 305 000=1.230 5×107;
(4)398.2 千万=3 982 000 000=3.982×109.
一个绝对值大于 10 的数都可记成 a×10n 的形式,其中 a 的取值范围 1≤a<10 .n 等于原数整数位减 1.这种记数方法叫做科学记数法.
科学记数法
概念
应用
表示绝对值大于 10 的数
根据科学记数法写原数
n 等于整数位数减 1
原数整数位数等于指数 n 加 1
课堂小结
同课章节目录
