3.4 第4课时 方案选择、分段计费与几何图形问题 课件 (共20张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 3.4 第4课时 方案选择、分段计费与几何图形问题 课件 (共20张PPT)初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 21:33:42 | ||
图片预览








文档简介
(共20张PPT)
第3章 一元一次方程
3.4 一元一次方程模型的应用
第4课时 方案选择、分段计费与几何图形问题
学习目标
1.理解题意,找出分段收费及盈不足问题的等量关系.(难点)
2.通过列一元一次方程解决分段收费及间隔问题、盈不足问题.(重点)
3.了解形积变化问题的意义,能分析题中已知数与未知数之间的相等关系,列出一元一次方程解简单的应用题.
动脑筋
新课导入
为鼓励居民节约用水,某市出台了新的家庭用水收费标准,规定:所交水费分为标准内水费与超标部分水费两部分,其中标准内水费为 1.96 元/ t,超标部分水费为2.94 元/t. 某家庭 6 月份用水 12 t,需交水费 27.44元. 求该市规定的家庭月标准用水量.
本问题首先要判断所交水费 27.44 元中是否含有超标部分,由于 1.96×12 = 23.52 (元),小于 27.44 元,
因此所交水费中含有超标部分的水费,即
月标准内水费 + 超标部分的水费 = 该月所交水费
设家庭月标准用水量为 x t,根据等量关系,得
1.96x + (12 - x)×2.94 = 27.44.
解得 x = 8.
因此,该市家庭月标准用水量为 8 t.
对应练习
为鼓励节约用电,某地用电收费标准规定:如果每户每月用
电不超过150 kW·h,那么1kW·h电按0.5元缴纳;超过部分则
按1kW·h电0.8元缴纳.如果小张家某月缴纳的电费为147.8元,
那么小张家该月用电多少?
0.8(x-150)+150×0.5=147.8.
解得 x=241.
答:小张家该月用电约241kw·h.
解:设小张家该月用电xkw·h,根据题意,得
解分段计费问题首先要考虑收费是在哪一段,所用水(电)是否超过标准.
如果在标准内,那么所交费用=标准内费率×所用水(电)量;如果超过标准,那么所交费用=标准内费用+超过标准的费用,即:所交费用=标准内费率×标准量+标准外费率×超过标准的量.
注意
例 4
例题讲解
现有树苗若干棵,计划栽在一段公路的一侧,要求路的两端各栽1棵,并且每2棵树的间隔相等. 方案一:如果每隔5m栽1棵,则树苗缺21棵;方案二:如果每隔5.5m栽1棵,则树苗正好完.根据以上方案,请算出原有树苗的棵数和这段路的长度.
分析 观察下面植树示意图,想一想:
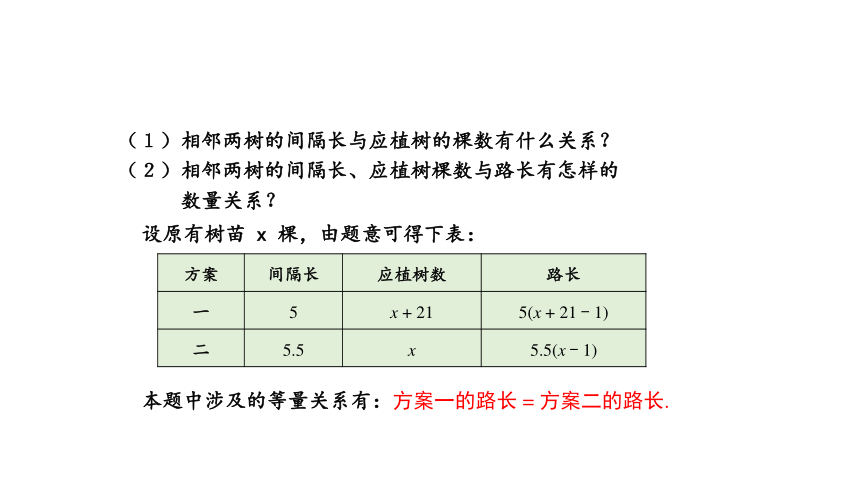
(1)相邻两树的间隔长与应植树的棵数有什么关系?
(2)相邻两树的间隔长、应植树棵数与路长有怎样的
数量关系?
设原有树苗 x 棵,由题意可得下表:
方案 间隔长 应植树数 路长
一 5 x + 21 5(x + 21 - 1)
二 5.5 x 5.5(x - 1)
本题中涉及的等量关系有:方案一的路长 = 方案二的路长.
解:设原有树苗 x 棵,根据等量关系,得
5(x + 21 - 1) = 5.5(x - 1) ,
即 5(x + 20) = 5.5(x - 1),
化简, 得 -0.5x = -105.5,
解得 x = 211.
因此,这段路长为 5×(211 + 20) = 1 155 (m).
答:原有树苗 211 棵,这段路的长度为 1 155 m.
对应练习
某道路一侧原有路灯106盏(两端都有),相邻两盏灯的距离为36m,
现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70m,则
需安装新型节能灯多少盏?
答:需安装新型节能灯55盏.
解:设需安装新型节能灯x盏,根据题意,得
解得 x=55.
70(x-1)=(106-1)×36.
间隔问题应用比较普遍,如路边种树,街道装路灯等.
需要注意:
(1)两个端点都种上树(装上灯),则树数-1=间隔数;
(2)两个端点都不种树(装上灯),则树数+1=间隔数.
注意
拓展:几何图形问题
等积(等长)变形问题
形状发生了变化,而体积(周长)没变,此时,相等关系是变化前后体积(周长)相等.
特别提醒
(1)列方程时结合题意找出变化过程中保持不变的量;
(2)设未知数时多将图形的长、宽、半径等设为未知数;
(3)列方程时要注意所有单位要统一.
补充练习
1.小明所在城市的“阶梯水价”收费办法是:每户用水不超过5 t,每吨水费x元;超过5 t,超过部分每吨加收2元,小明家今年5月份用水9 t,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44 B.5x+4(x-2)=44
C.9(x+2)=44 D.9(x+2)-4×2=44
A
2.某市生活拨号上网有两种收费方式,用户可以任选 其一. A计时制:0.05 元/分钟;B包月制:60 元/月 (限一部个人住宅电话上网). 此外,两种上网方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种收费方式下该用户应该支付的费用.
解:(1)采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
解:(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,上网
时间越长,采用包月制越合算.所以,
当 0 < x < 20 时,采用计时制合算;
当 x=20 时,采用两种方式费用相同;
当 x > 20 时,采用包月制合算.
2.某市生活拨号上网有两种收费方式,用户可以任选 其一. A计时制:0.05 元/分钟;B包月制:60 元/月 (限一部个人住宅电话上网). 此外,两种上网方式都得加收通信费 0.02 元/分钟.
(2) 你认为采用哪种方式比较合算?
3. 用A4纸在某复印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.
问:如何根据复印的页数选择复印的地点使总价格比较便宜? (复印的页数不为零)
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x,依题意,列表得:
(3) 当 x 大于20时,依题意得
2.4+0.09(x-20) = 0.1 x.
解得 x = 60
所以,当x大于20且小于60时,图书馆价格便宜;
当x等于60时,两者价格相同;
当x大于60时,复印社价格便宜.
综上所述:当 x 小于60页时,图书馆价格便宜;
当 x 等于60时,两者价格相同;
当 x 大于60时,复印社价格便宜.
(1) 当 x <20 时,0.12x 大于 0.1x 恒成立,图书馆价格便宜;
(2) 当 x = 20 时,图书馆价格便宜;
4.如图所示,将一个正方形纸片剪去一个宽为5 cm的长条后,再从剩下的长方形纸片上剪去一个宽为6 cm的长条.
(1)如果两次剪下的长条面积正好相等,那么这个正方形纸片的面积多少
解:(1)设正方形纸片的边长为x cm,
依题意,得5x=6(x-5),解得x=30,
所以30×30=900(cm2).
故这个正方形纸片的面积是900 cm2.
5 cm
6 cm
4.如图所示,将一个正方形纸片剪去一个宽为5 cm的长条后,再从剩下的长方形纸片上剪去一个宽为6 cm的长条.
(2)第二次剪下的长条的面积能是第一次剪下的长条的面积的2倍吗 如果能,请求出正方形纸片的面积;如果不能,请说明理由.
解:(2)不能.理由如下:
设正方形纸片的边长为y cm,
依题意,得2×5y=6(y-5),
解得y=-7.5.
因为不符合实际,所以不能.
5 cm
6 cm
分段计费问题
方案问题
几何图形问题
一元一次方程模型的应用
课堂小结
第3章 一元一次方程
3.4 一元一次方程模型的应用
第4课时 方案选择、分段计费与几何图形问题
学习目标
1.理解题意,找出分段收费及盈不足问题的等量关系.(难点)
2.通过列一元一次方程解决分段收费及间隔问题、盈不足问题.(重点)
3.了解形积变化问题的意义,能分析题中已知数与未知数之间的相等关系,列出一元一次方程解简单的应用题.
动脑筋
新课导入
为鼓励居民节约用水,某市出台了新的家庭用水收费标准,规定:所交水费分为标准内水费与超标部分水费两部分,其中标准内水费为 1.96 元/ t,超标部分水费为2.94 元/t. 某家庭 6 月份用水 12 t,需交水费 27.44元. 求该市规定的家庭月标准用水量.
本问题首先要判断所交水费 27.44 元中是否含有超标部分,由于 1.96×12 = 23.52 (元),小于 27.44 元,
因此所交水费中含有超标部分的水费,即
月标准内水费 + 超标部分的水费 = 该月所交水费
设家庭月标准用水量为 x t,根据等量关系,得
1.96x + (12 - x)×2.94 = 27.44.
解得 x = 8.
因此,该市家庭月标准用水量为 8 t.
对应练习
为鼓励节约用电,某地用电收费标准规定:如果每户每月用
电不超过150 kW·h,那么1kW·h电按0.5元缴纳;超过部分则
按1kW·h电0.8元缴纳.如果小张家某月缴纳的电费为147.8元,
那么小张家该月用电多少?
0.8(x-150)+150×0.5=147.8.
解得 x=241.
答:小张家该月用电约241kw·h.
解:设小张家该月用电xkw·h,根据题意,得
解分段计费问题首先要考虑收费是在哪一段,所用水(电)是否超过标准.
如果在标准内,那么所交费用=标准内费率×所用水(电)量;如果超过标准,那么所交费用=标准内费用+超过标准的费用,即:所交费用=标准内费率×标准量+标准外费率×超过标准的量.
注意
例 4
例题讲解
现有树苗若干棵,计划栽在一段公路的一侧,要求路的两端各栽1棵,并且每2棵树的间隔相等. 方案一:如果每隔5m栽1棵,则树苗缺21棵;方案二:如果每隔5.5m栽1棵,则树苗正好完.根据以上方案,请算出原有树苗的棵数和这段路的长度.
分析 观察下面植树示意图,想一想:
(1)相邻两树的间隔长与应植树的棵数有什么关系?
(2)相邻两树的间隔长、应植树棵数与路长有怎样的
数量关系?
设原有树苗 x 棵,由题意可得下表:
方案 间隔长 应植树数 路长
一 5 x + 21 5(x + 21 - 1)
二 5.5 x 5.5(x - 1)
本题中涉及的等量关系有:方案一的路长 = 方案二的路长.
解:设原有树苗 x 棵,根据等量关系,得
5(x + 21 - 1) = 5.5(x - 1) ,
即 5(x + 20) = 5.5(x - 1),
化简, 得 -0.5x = -105.5,
解得 x = 211.
因此,这段路长为 5×(211 + 20) = 1 155 (m).
答:原有树苗 211 棵,这段路的长度为 1 155 m.
对应练习
某道路一侧原有路灯106盏(两端都有),相邻两盏灯的距离为36m,
现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70m,则
需安装新型节能灯多少盏?
答:需安装新型节能灯55盏.
解:设需安装新型节能灯x盏,根据题意,得
解得 x=55.
70(x-1)=(106-1)×36.
间隔问题应用比较普遍,如路边种树,街道装路灯等.
需要注意:
(1)两个端点都种上树(装上灯),则树数-1=间隔数;
(2)两个端点都不种树(装上灯),则树数+1=间隔数.
注意
拓展:几何图形问题
等积(等长)变形问题
形状发生了变化,而体积(周长)没变,此时,相等关系是变化前后体积(周长)相等.
特别提醒
(1)列方程时结合题意找出变化过程中保持不变的量;
(2)设未知数时多将图形的长、宽、半径等设为未知数;
(3)列方程时要注意所有单位要统一.
补充练习
1.小明所在城市的“阶梯水价”收费办法是:每户用水不超过5 t,每吨水费x元;超过5 t,超过部分每吨加收2元,小明家今年5月份用水9 t,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44 B.5x+4(x-2)=44
C.9(x+2)=44 D.9(x+2)-4×2=44
A
2.某市生活拨号上网有两种收费方式,用户可以任选 其一. A计时制:0.05 元/分钟;B包月制:60 元/月 (限一部个人住宅电话上网). 此外,两种上网方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种收费方式下该用户应该支付的费用.
解:(1)采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
解:(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,上网
时间越长,采用包月制越合算.所以,
当 0 < x < 20 时,采用计时制合算;
当 x=20 时,采用两种方式费用相同;
当 x > 20 时,采用包月制合算.
2.某市生活拨号上网有两种收费方式,用户可以任选 其一. A计时制:0.05 元/分钟;B包月制:60 元/月 (限一部个人住宅电话上网). 此外,两种上网方式都得加收通信费 0.02 元/分钟.
(2) 你认为采用哪种方式比较合算?
3. 用A4纸在某复印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.
问:如何根据复印的页数选择复印的地点使总价格比较便宜? (复印的页数不为零)
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x,依题意,列表得:
(3) 当 x 大于20时,依题意得
2.4+0.09(x-20) = 0.1 x.
解得 x = 60
所以,当x大于20且小于60时,图书馆价格便宜;
当x等于60时,两者价格相同;
当x大于60时,复印社价格便宜.
综上所述:当 x 小于60页时,图书馆价格便宜;
当 x 等于60时,两者价格相同;
当 x 大于60时,复印社价格便宜.
(1) 当 x <20 时,0.12x 大于 0.1x 恒成立,图书馆价格便宜;
(2) 当 x = 20 时,图书馆价格便宜;
4.如图所示,将一个正方形纸片剪去一个宽为5 cm的长条后,再从剩下的长方形纸片上剪去一个宽为6 cm的长条.
(1)如果两次剪下的长条面积正好相等,那么这个正方形纸片的面积多少
解:(1)设正方形纸片的边长为x cm,
依题意,得5x=6(x-5),解得x=30,
所以30×30=900(cm2).
故这个正方形纸片的面积是900 cm2.
5 cm
6 cm
4.如图所示,将一个正方形纸片剪去一个宽为5 cm的长条后,再从剩下的长方形纸片上剪去一个宽为6 cm的长条.
(2)第二次剪下的长条的面积能是第一次剪下的长条的面积的2倍吗 如果能,请求出正方形纸片的面积;如果不能,请说明理由.
解:(2)不能.理由如下:
设正方形纸片的边长为y cm,
依题意,得2×5y=6(y-5),
解得y=-7.5.
因为不符合实际,所以不能.
5 cm
6 cm
分段计费问题
方案问题
几何图形问题
一元一次方程模型的应用
课堂小结
同课章节目录
