4.2 第2课时 线段长短的比较 课件 (共19张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 4.2 第2课时 线段长短的比较 课件 (共19张PPT)初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第4章 图形的认识
4.2 线段、射线、直线
第2课时 线段长短的比较
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两
条线段的长短. (重点)
2. 理解线段等分点的意义.
3. 能够运用线段的和、差、倍、分关系求线段的
长度. (重点、难点)
4. 体会文字语言、符号语言和图形语言的相互转化.
5. 了解两点间距离的意义,理解“两点之间,线段
最短”的线段性质,并学会运用. (难点)
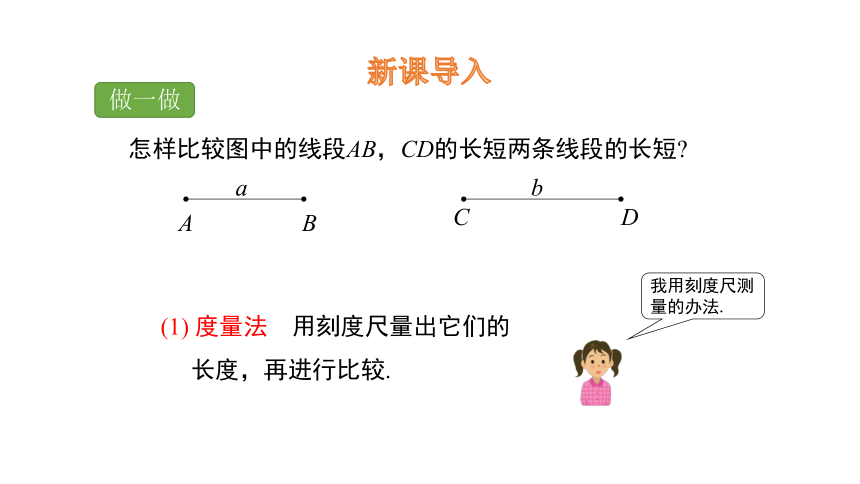
做一做
新课导入
怎样比较图中的线段AB,CD的长短两条线段的长短
(1) 度量法 用刻度尺量出它们的
长度,再进行比较.
A B
C D
a
b
我用刻度尺测量的办法.
把其中一条线段移到另一条上作比较.
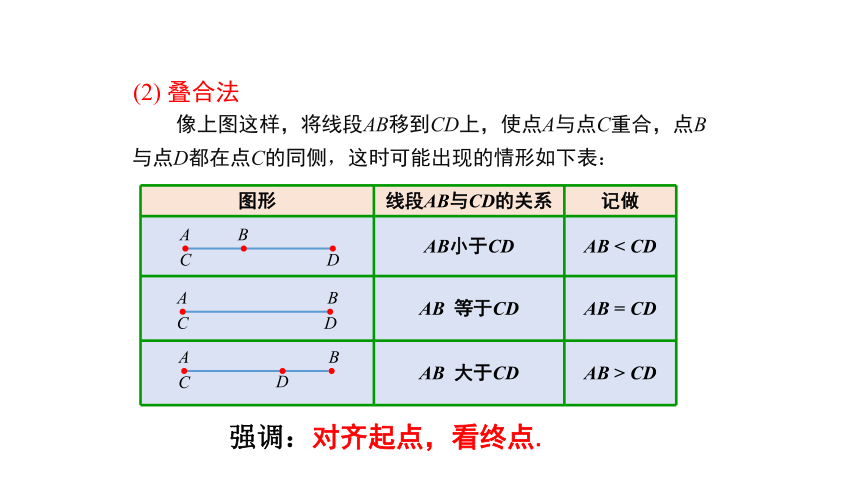
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
强调:对齐起点,看终点.
像上图这样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
AB小于CD AB < CD
AB 等于CD AB = CD
AB 大于CD AB > CD
C
A
D
B
C
A
D
B
C
A
D
B
(2) 叠合法
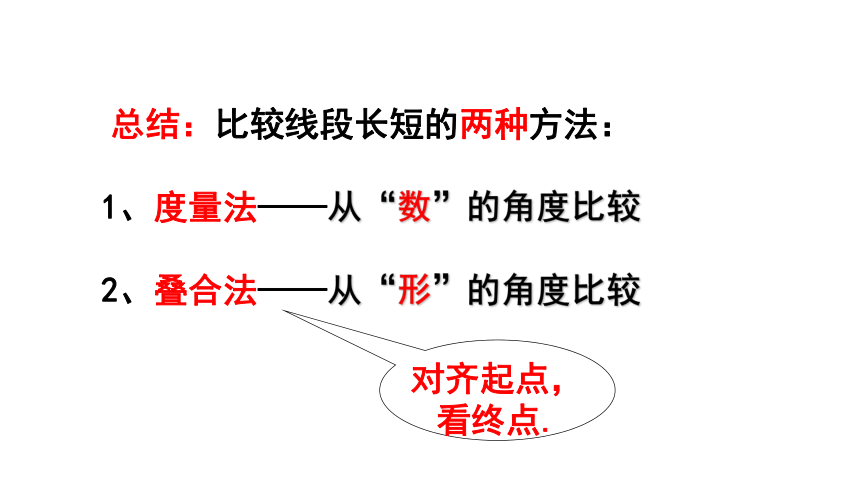
总结:比较线段长短的两种方法:
1、度量法——从“数”的角度比较
2、叠合法——从“形”的角度比较
对齐起点,看终点.
如图,点C 落在线段AB的延长线(即以A为
端点,方向为A到B的射线)上,
A
B
C
a
设AB=a ,AC=b, BC=c ,
则线段AC就是a与c的和,记做b = a + c ;
线段BC就是b与a的差,记做c = b - a.
c
b
动脑筋
杭州湾跨海大桥是跨越杭州湾的便捷通道. 大桥北起嘉兴市,跨越宽阔的杭州湾海域后止于宁波市,全长36km. 大桥建成后宁波至上海间的陆路距离缩短了约120km. 你知道这是根据什么原理吗?
人们根据长期实践经验得到以下基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间线段最短.
连接两点的线段的长度,叫做这两点间的距离.
A
B
线段AB最短.
例 1
例题讲解
如图,已知线段a,借助圆规和直尺作一条线段
使它等于2a.
A
a
C
作法:
(1)作射线AD;
(2)在AD上顺次截取AB=BC=a.
则AC就是所要求作的线段.
D
这样仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
B
若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
类似地,线段还有三等分点,四等分点.
点B是线段AC的中点
AB=BC=0.5AC
线段的三等分点
线段的四等分点
A
C
D
B
例 2
如图,已知线段 a,b (a > b)作一条线段使
它等于a - b.
作法:
A
b
(1) 作射线 AF;
F
(2) 在射线 AF 上截取 AC = a;
a
C
B
(3) 在线段 AC 截取 AB = b.
则线段 BC 就是所要求作的线段(如图).
1.如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B
B.A→C→F→B
C.A→C→E→F→B
D.A→C→M→B
B
随 堂 小 测
2.下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
3.比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
D
A
4.点B在直线AC上,线段AB=5,BC=3,则A,C两点间的
距离是( )
A.8 B.2 C.8或2 D.无法确定
C
5.点C在线段AB上,下列条件中不能确定点C是线段AB中点的是( )
A.AC=BC B.AC+BC=AB
C.AB=2AC D.BC= AB
B
6.如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
B
7.某同学用剪刀沿直线将一片平整的银杏叶剪
掉一部分,发现剩下的银杏叶的周长比原银杏
叶的周长要小,能正确解释这一现象的数学知
识是 .
两点之间线段最短
8.在直线l上顺次取A,B,C三点,使得AB=4 cm,BC=3 cm.如果点O是线段AC的中点,那么线段OB= cm.
0.5
9.如图所示,若BC =CD,则 BD = CD,BC = BD,BC CE,AC CD(最后两空填“>”“<”或“=”).
解析:因为BC=CD,
所以BD= BC+ CD= CD +CD=2CD,所以BC= BD.
BC= CD= CE - DE< CE,AC=AB +BC=AB + CD > CD.
2
<
>
课堂小结
比较线段的长短
线段的性质
比较线段长短的方法
用尺规作一条线段等于已知线段
线段的中点
两点之间线段最短
两点之间的距离
叠合法
度量法
作一条线段等于已知线段
线段的和差
第4章 图形的认识
4.2 线段、射线、直线
第2课时 线段长短的比较
学习目标
1. 会用尺规画一条线段等于已知线段,会比较两
条线段的长短. (重点)
2. 理解线段等分点的意义.
3. 能够运用线段的和、差、倍、分关系求线段的
长度. (重点、难点)
4. 体会文字语言、符号语言和图形语言的相互转化.
5. 了解两点间距离的意义,理解“两点之间,线段
最短”的线段性质,并学会运用. (难点)
做一做
新课导入
怎样比较图中的线段AB,CD的长短两条线段的长短
(1) 度量法 用刻度尺量出它们的
长度,再进行比较.
A B
C D
a
b
我用刻度尺测量的办法.
把其中一条线段移到另一条上作比较.
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
强调:对齐起点,看终点.
像上图这样,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,这时可能出现的情形如下表:
图形 线段AB与CD的关系 记做
AB小于CD AB < CD
AB 等于CD AB = CD
AB 大于CD AB > CD
C
A
D
B
C
A
D
B
C
A
D
B
(2) 叠合法
总结:比较线段长短的两种方法:
1、度量法——从“数”的角度比较
2、叠合法——从“形”的角度比较
对齐起点,看终点.
如图,点C 落在线段AB的延长线(即以A为
端点,方向为A到B的射线)上,
A
B
C
a
设AB=a ,AC=b, BC=c ,
则线段AC就是a与c的和,记做b = a + c ;
线段BC就是b与a的差,记做c = b - a.
c
b
动脑筋
杭州湾跨海大桥是跨越杭州湾的便捷通道. 大桥北起嘉兴市,跨越宽阔的杭州湾海域后止于宁波市,全长36km. 大桥建成后宁波至上海间的陆路距离缩短了约120km. 你知道这是根据什么原理吗?
人们根据长期实践经验得到以下基本事实:
两点之间的所有连线中,线段最短.
简单说成:两点之间线段最短.
连接两点的线段的长度,叫做这两点间的距离.
A
B
线段AB最短.
例 1
例题讲解
如图,已知线段a,借助圆规和直尺作一条线段
使它等于2a.
A
a
C
作法:
(1)作射线AD;
(2)在AD上顺次截取AB=BC=a.
则AC就是所要求作的线段.
D
这样仅用圆规和没有刻度的直尺作图的方法叫尺规作图.
B
若点B在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.
类似地,线段还有三等分点,四等分点.
点B是线段AC的中点
AB=BC=0.5AC
线段的三等分点
线段的四等分点
A
C
D
B
例 2
如图,已知线段 a,b (a > b)作一条线段使
它等于a - b.
作法:
A
b
(1) 作射线 AF;
F
(2) 在射线 AF 上截取 AC = a;
a
C
B
(3) 在线段 AC 截取 AB = b.
则线段 BC 就是所要求作的线段(如图).
1.如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B
B.A→C→F→B
C.A→C→E→F→B
D.A→C→M→B
B
随 堂 小 测
2.下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
3.比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
D
A
4.点B在直线AC上,线段AB=5,BC=3,则A,C两点间的
距离是( )
A.8 B.2 C.8或2 D.无法确定
C
5.点C在线段AB上,下列条件中不能确定点C是线段AB中点的是( )
A.AC=BC B.AC+BC=AB
C.AB=2AC D.BC= AB
B
6.如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
B
7.某同学用剪刀沿直线将一片平整的银杏叶剪
掉一部分,发现剩下的银杏叶的周长比原银杏
叶的周长要小,能正确解释这一现象的数学知
识是 .
两点之间线段最短
8.在直线l上顺次取A,B,C三点,使得AB=4 cm,BC=3 cm.如果点O是线段AC的中点,那么线段OB= cm.
0.5
9.如图所示,若BC =CD,则 BD = CD,BC = BD,BC CE,AC CD(最后两空填“>”“<”或“=”).
解析:因为BC=CD,
所以BD= BC+ CD= CD +CD=2CD,所以BC= BD.
BC= CD= CE - DE< CE,AC=AB +BC=AB + CD > CD.
2
<
>
课堂小结
比较线段的长短
线段的性质
比较线段长短的方法
用尺规作一条线段等于已知线段
线段的中点
两点之间线段最短
两点之间的距离
叠合法
度量法
作一条线段等于已知线段
线段的和差
同课章节目录
