4.3.2 第2课时 余角与补角 课件 (共18张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 4.3.2 第2课时 余角与补角 课件 (共18张PPT)初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 866.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
第4章 图形的认识
4.3 角
4.3.2 角的度量与计算
第2课时 余角与补角
学习目标
1. 了解余角、补角的概念,掌握余角和补角的性质.
(重点)
2. 能利用余角、补角的知识解决相关问题.(难点)
新课导入
做一做
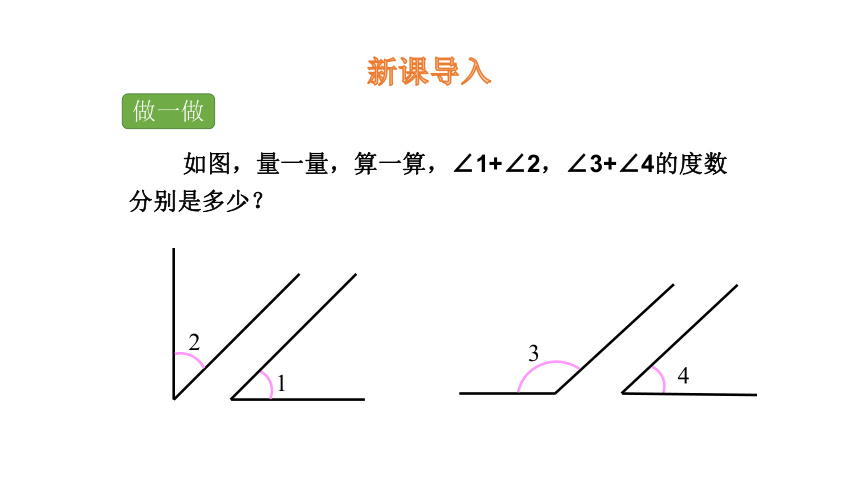
如图,量一量,算一算,∠1+∠2,∠3+∠4的度数分别是多少?
1
2
3
4
1
2
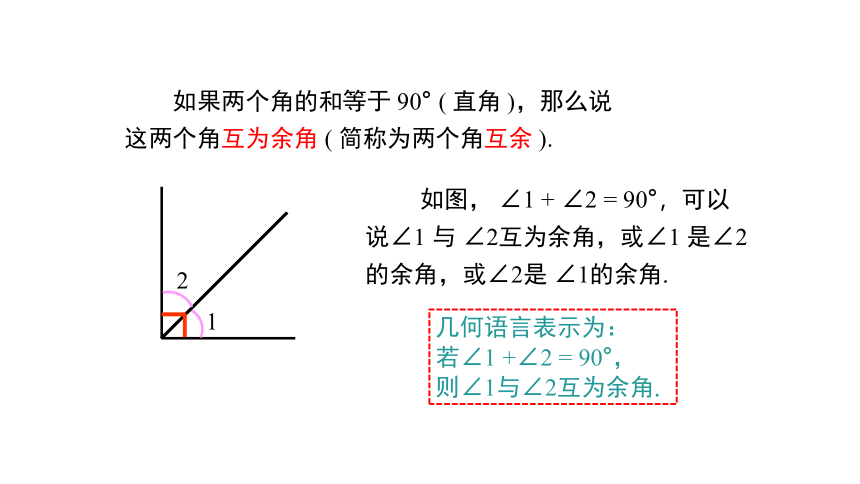
如果两个角的和等于 90° ( 直角 ),那么说这两个角互为余角 ( 简称为两个角互余 ).
如图, ∠1 + ∠2 = 90°,可以说∠1 与 ∠2互为余角,或∠1 是∠2的余角,或∠2是 ∠1的余角.
几何语言表示为:
若∠1 +∠2 = 90°,
则∠1与∠2互为余角.
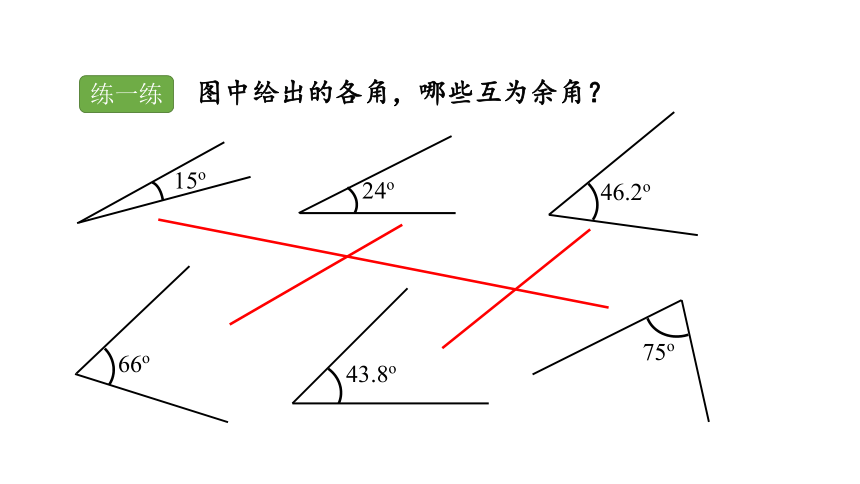
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
练一练
3
4
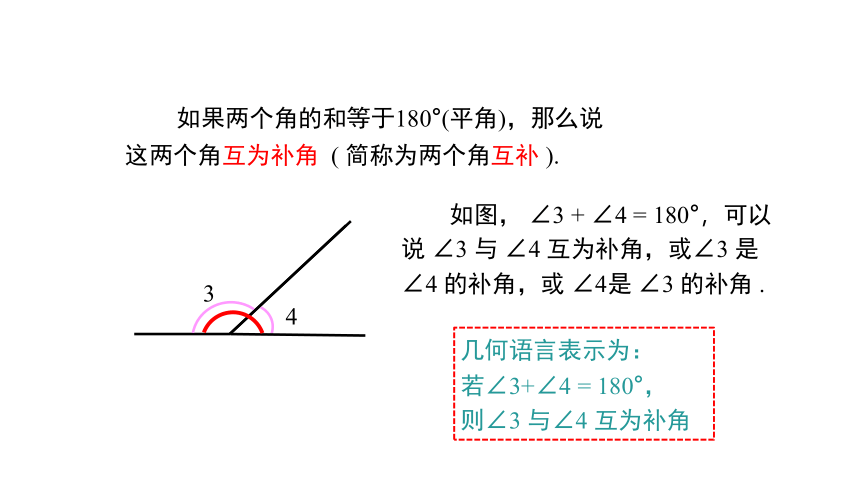
如果两个角的和等于180°(平角),那么说这两个角互为补角 ( 简称为两个角互补 ).
如图, ∠3 + ∠4 = 180°,可以说 ∠3 与 ∠4 互为补角,或∠3 是 ∠4 的补角,或 ∠4是 ∠3 的补角 .
几何语言表示为:
若∠3+∠4 = 180°,
则∠3 与∠4 互为补角
练一练
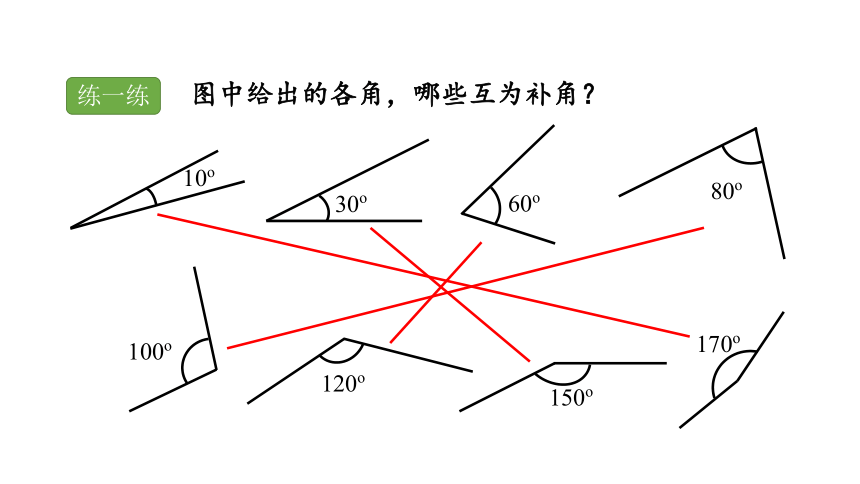
图中给出的各角,哪些互为补角?
10o
30o
60o
80o
120o
150o
100o
170o
动脑筋
(1)如图(a),∠1与∠2互补,∠1与∠3互补, 那么∠2与∠3的大小有什么关系?
(a)
由于 ∠1 +∠2 = 180°,∠1 +∠3 =180°,
所以 ∠2 = 180°-∠1,∠3 = 180°-∠1.
因此 ∠2 =∠3(等量代换).
于是,我们得出:
同角(或等角)的补角相等.
(2)如图(b),∠4与∠5互余,∠4与∠6互余,
那么∠5与∠6的大小有什么关系?
(b)
类似地,我们可以得到 ∠5 = ∠6,
于是有:
同角或等角的余角相等.
例 4
例题讲解
如图,∠AOB与∠BOD互为余角,OC是∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
解 因为∠AOB与∠BOD互为余角,
所以∠BOD = 90°-∠AOB= 90°-29.66°= 60.34°.
又因为OC是∠BOD的平分线,
因此,∠COD 的度数为 30.17°.
所以
已知一个角的余角是这个角的补角的 ,求这个角的度数.
解 设这个角为x°,则这个角的余角为(90-x)°,
补角为(180-x)°.
根据题意,得 ,
解得x = 45 .
因此,这个角的度数为45°.
例 5
随 堂 小 测
1. 若∠A=23°,则∠A余角的大小是( )
A.57° B.67°
C.77° D.157°
2.若α=70°,则α的补角的度数是( )
A.130° B.110°
C.30° D.20°
B
B
3.下列说法正确的有 ( )
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
B
4.若∠A与∠B互为余角,∠A=30°,则∠B的补角是( )
A.60° B.120° C.30° D.150°
5.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
A.互补
B.互余
C.相等
D.无法确定
B
C
6.下列说法中,正确的有________.(填序号)
①钝角与锐角互补;
②∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
7. 若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x°,则它的补角是 (180-x)°,
余角是 (90-x)°.
根据题意,得 180-x = 4(90-x).
解得 x = 60.
答:这个角的度数是 60°.
8.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
解:设∠AOB=x,因为∠AOC与∠AOB互补,
所以∠AOC=180°-x.
因为OM,ON分别为∠AOC,∠AOB的平分线,
所以(180°-x)-x=40 °,解得x=50°,
则180°-x=130°.即∠AOB=50°,∠AOC=130°.
O
D
A
B
C
N
M
课堂小结
互余 互补
两角间的数量关系
对应图形
性质
同角或等角的
补角相等
同角或等角的
余角相等
第4章 图形的认识
4.3 角
4.3.2 角的度量与计算
第2课时 余角与补角
学习目标
1. 了解余角、补角的概念,掌握余角和补角的性质.
(重点)
2. 能利用余角、补角的知识解决相关问题.(难点)
新课导入
做一做
如图,量一量,算一算,∠1+∠2,∠3+∠4的度数分别是多少?
1
2
3
4
1
2
如果两个角的和等于 90° ( 直角 ),那么说这两个角互为余角 ( 简称为两个角互余 ).
如图, ∠1 + ∠2 = 90°,可以说∠1 与 ∠2互为余角,或∠1 是∠2的余角,或∠2是 ∠1的余角.
几何语言表示为:
若∠1 +∠2 = 90°,
则∠1与∠2互为余角.
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
练一练
3
4
如果两个角的和等于180°(平角),那么说这两个角互为补角 ( 简称为两个角互补 ).
如图, ∠3 + ∠4 = 180°,可以说 ∠3 与 ∠4 互为补角,或∠3 是 ∠4 的补角,或 ∠4是 ∠3 的补角 .
几何语言表示为:
若∠3+∠4 = 180°,
则∠3 与∠4 互为补角
练一练
图中给出的各角,哪些互为补角?
10o
30o
60o
80o
120o
150o
100o
170o
动脑筋
(1)如图(a),∠1与∠2互补,∠1与∠3互补, 那么∠2与∠3的大小有什么关系?
(a)
由于 ∠1 +∠2 = 180°,∠1 +∠3 =180°,
所以 ∠2 = 180°-∠1,∠3 = 180°-∠1.
因此 ∠2 =∠3(等量代换).
于是,我们得出:
同角(或等角)的补角相等.
(2)如图(b),∠4与∠5互余,∠4与∠6互余,
那么∠5与∠6的大小有什么关系?
(b)
类似地,我们可以得到 ∠5 = ∠6,
于是有:
同角或等角的余角相等.
例 4
例题讲解
如图,∠AOB与∠BOD互为余角,OC是∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
解 因为∠AOB与∠BOD互为余角,
所以∠BOD = 90°-∠AOB= 90°-29.66°= 60.34°.
又因为OC是∠BOD的平分线,
因此,∠COD 的度数为 30.17°.
所以
已知一个角的余角是这个角的补角的 ,求这个角的度数.
解 设这个角为x°,则这个角的余角为(90-x)°,
补角为(180-x)°.
根据题意,得 ,
解得x = 45 .
因此,这个角的度数为45°.
例 5
随 堂 小 测
1. 若∠A=23°,则∠A余角的大小是( )
A.57° B.67°
C.77° D.157°
2.若α=70°,则α的补角的度数是( )
A.130° B.110°
C.30° D.20°
B
B
3.下列说法正确的有 ( )
①锐角的余角是锐角,锐角的补角是锐角;
②直角没有补角;
③钝角没有余角,钝角的补角是锐角;
④直角的补角还是直角;
⑤一个角的补角与它的余角的差为90°;
⑥两个角相等,它们的补角也相等.
A.3个 B.4个 C.5个 D.6个
B
4.若∠A与∠B互为余角,∠A=30°,则∠B的补角是( )
A.60° B.120° C.30° D.150°
5.如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
A.互补
B.互余
C.相等
D.无法确定
B
C
6.下列说法中,正确的有________.(填序号)
①钝角与锐角互补;
②∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
7. 若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x°,则它的补角是 (180-x)°,
余角是 (90-x)°.
根据题意,得 180-x = 4(90-x).
解得 x = 60.
答:这个角的度数是 60°.
8.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
解:设∠AOB=x,因为∠AOC与∠AOB互补,
所以∠AOC=180°-x.
因为OM,ON分别为∠AOC,∠AOB的平分线,
所以(180°-x)-x=40 °,解得x=50°,
则180°-x=130°.即∠AOB=50°,∠AOC=130°.
O
D
A
B
C
N
M
课堂小结
互余 互补
两角间的数量关系
对应图形
性质
同角或等角的
补角相等
同角或等角的
余角相等
同课章节目录
