4.3.1 角与角的大小比较 课件 (共22张PPT)初中数学湘教版七年级上册
文档属性
| 名称 | 4.3.1 角与角的大小比较 课件 (共22张PPT)初中数学湘教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1016.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第4章 图形的认识
4.3 角
4.3.1 角与角的大小比较
学习目标
1.理解角的概念,掌握角的表示方法;
2.理解角的平分线.(重点、难点)
新课导入
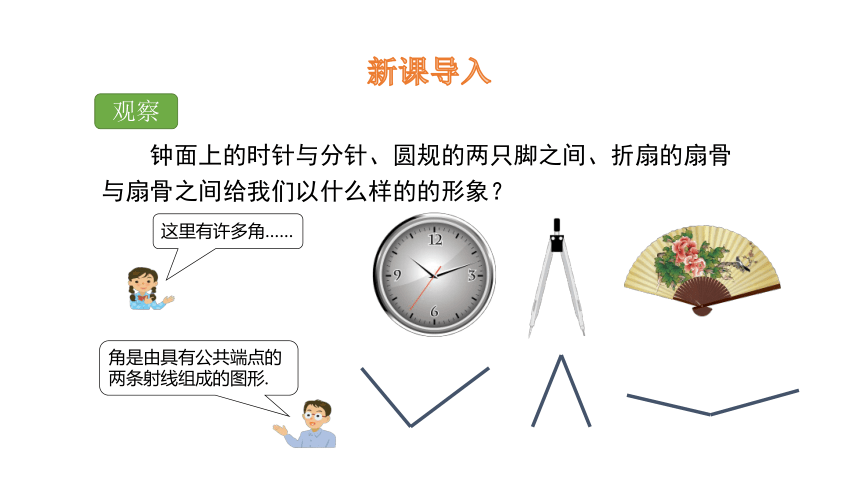
钟面上的时针与分针、圆规的两只脚之间、折扇的扇骨与扇骨之间给我们以什么样的的形象?
观察
这里有许多角……
角是由具有公共端点的两条射线组成的图形.
①静态概念:角是由具有公共端点的两条射线组成的图形.
A
O
B
终边
角的内部
始边
②动态概念:角是由一条射线绕着它的端点从一个位置旋转到另一个位置时 所成的图形.
这条射线的端点O叫做角的顶点.
射线原来所在的位置OA叫做角的始边,
旋转后的位置OB叫做角的终边,
角的始边和终边统称为角的边.
从始边旋转到终边所扫过的区域叫做角的内部.
角的概念
当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角(如图).
B
O
A
平角
(B)
A
O
周角
注意:角的大小由角的始边绕顶点旋转至终边时旋转的量
的大小决定.
当射线绕着端点旋转一周,又重新回到原来的位置时,所成的角叫做周角(如图).
做一做
1.判断正误.
(1)有公共端点的两条射线叫做角.( )
(2)两条射线组成的图形叫做角.( )
(3)角的大小与角画出的两边的长短无关.( )
(4)由一条射线绕一点旋转而形成的图形叫做角.( )
×
×
√
×
2.判断下列哪些图形是角.
√
×
√
√
角通常可用如图的方法来表示.
1
O
A
B
∠AOB,∠BOA 或∠O
∠ 1
注:顶点的字母必须写在中间.
注:当两个或两个以上的角有同一个顶点时,不能用一个大写字母表示.
角的表示方法总结
方法 图示 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 ∠α ∠1 有弧线和数字,
弧线和小写希腊字母
O
A
B
O
1
α
找一找
如图,写出符合以下条件的角:
(1)能用一个大写字母表示的角;
(2)以A为顶点的角.
解:(1)∠B,∠C.
(2)∠BAC,∠BAD,∠CAD.
怎样比较图中∠ABC和∠DEF的大小?
F
E
D
C
B
A
探究
可用量角器量.
与线段长短的比较类似,可以把它们叠合在一起比较大小.
度量法
叠合法
先将∠DEF移动,使它的顶点E与∠ABC的顶点B重合,并且使∠DEF的一条边EF与∠ABC的一条边BC重合,边ED,BA都在BC的同侧.这时可能出现的情形如下表:
情形 图形 ∠ABC与∠DEF的关系
ED与BA重合 ∠ABC =∠DEF
ED落在∠ABC内部 ∠ABC >∠DEF
ED落在∠ABC外部 ∠ABC <∠DEF
A(D)
C(F)
B(E)
A
C(F)
B(E)
D
D
C(F)
B(E)
A
如图,如果∠AOB=∠COD,那么( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.以上都不对
B
比一比
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,这条射线叫做这个角的平分线.
若OC是∠AOB的角平分线,
则∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
几何语言
O
B
A
C
如图:OC 是∠AOB 的平分线,OD 是∠BOC 的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
做一做
随 堂 小 测
1. 如图,下列说法:
(1)∠ECG和∠C是同一个角;
(2)∠OGF和∠DGB是同一个角;
(3)∠DOF和∠EOG是同一个角;
(4)∠ABC和∠ACB不是同一个角.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
C
3.在∠AOB的内部任取一点C,作射线OC,那么
有( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠BOC>∠AOB D.∠AOB>∠AOC
D
2.下列说法正确的是( )
A.一条直线就是一个平角
B.一个角的两边画得越长,这个角就越大
C.反向延长射线OA就得到一个平角
D.画一条射线就得到周角
C
4.下图中表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
5.如图所示,若有∠BAD=∠CAD,∠BCE=∠ACE,则下列
结论中错误的是( )
A.AD是∠BAC的平分线
B.CE是∠ACD的平分线
C.∠BCE= ∠ACB
D.CE是∠ABC的平分线
D
6.如图,点O在直线AB上,射线OC平分∠BOD,
若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
C
7、图中共有几个角?
( )个角 ( )个角 ( )个角 ( )个角
3
6
10
45
课堂小结
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
第4章 图形的认识
4.3 角
4.3.1 角与角的大小比较
学习目标
1.理解角的概念,掌握角的表示方法;
2.理解角的平分线.(重点、难点)
新课导入
钟面上的时针与分针、圆规的两只脚之间、折扇的扇骨与扇骨之间给我们以什么样的的形象?
观察
这里有许多角……
角是由具有公共端点的两条射线组成的图形.
①静态概念:角是由具有公共端点的两条射线组成的图形.
A
O
B
终边
角的内部
始边
②动态概念:角是由一条射线绕着它的端点从一个位置旋转到另一个位置时 所成的图形.
这条射线的端点O叫做角的顶点.
射线原来所在的位置OA叫做角的始边,
旋转后的位置OB叫做角的终边,
角的始边和终边统称为角的边.
从始边旋转到终边所扫过的区域叫做角的内部.
角的概念
当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角(如图).
B
O
A
平角
(B)
A
O
周角
注意:角的大小由角的始边绕顶点旋转至终边时旋转的量
的大小决定.
当射线绕着端点旋转一周,又重新回到原来的位置时,所成的角叫做周角(如图).
做一做
1.判断正误.
(1)有公共端点的两条射线叫做角.( )
(2)两条射线组成的图形叫做角.( )
(3)角的大小与角画出的两边的长短无关.( )
(4)由一条射线绕一点旋转而形成的图形叫做角.( )
×
×
√
×
2.判断下列哪些图形是角.
√
×
√
√
角通常可用如图的方法来表示.
1
O
A
B
∠AOB,∠BOA 或∠O
∠ 1
注:顶点的字母必须写在中间.
注:当两个或两个以上的角有同一个顶点时,不能用一个大写字母表示.
角的表示方法总结
方法 图示 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 ∠α ∠1 有弧线和数字,
弧线和小写希腊字母
O
A
B
O
1
α
找一找
如图,写出符合以下条件的角:
(1)能用一个大写字母表示的角;
(2)以A为顶点的角.
解:(1)∠B,∠C.
(2)∠BAC,∠BAD,∠CAD.
怎样比较图中∠ABC和∠DEF的大小?
F
E
D
C
B
A
探究
可用量角器量.
与线段长短的比较类似,可以把它们叠合在一起比较大小.
度量法
叠合法
先将∠DEF移动,使它的顶点E与∠ABC的顶点B重合,并且使∠DEF的一条边EF与∠ABC的一条边BC重合,边ED,BA都在BC的同侧.这时可能出现的情形如下表:
情形 图形 ∠ABC与∠DEF的关系
ED与BA重合 ∠ABC =∠DEF
ED落在∠ABC内部 ∠ABC >∠DEF
ED落在∠ABC外部 ∠ABC <∠DEF
A(D)
C(F)
B(E)
A
C(F)
B(E)
D
D
C(F)
B(E)
A
如图,如果∠AOB=∠COD,那么( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.以上都不对
B
比一比
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,这条射线叫做这个角的平分线.
若OC是∠AOB的角平分线,
则∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
几何语言
O
B
A
C
如图:OC 是∠AOB 的平分线,OD 是∠BOC 的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
做一做
随 堂 小 测
1. 如图,下列说法:
(1)∠ECG和∠C是同一个角;
(2)∠OGF和∠DGB是同一个角;
(3)∠DOF和∠EOG是同一个角;
(4)∠ABC和∠ACB不是同一个角.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
C
3.在∠AOB的内部任取一点C,作射线OC,那么
有( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠BOC>∠AOB D.∠AOB>∠AOC
D
2.下列说法正确的是( )
A.一条直线就是一个平角
B.一个角的两边画得越长,这个角就越大
C.反向延长射线OA就得到一个平角
D.画一条射线就得到周角
C
4.下图中表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
5.如图所示,若有∠BAD=∠CAD,∠BCE=∠ACE,则下列
结论中错误的是( )
A.AD是∠BAC的平分线
B.CE是∠ACD的平分线
C.∠BCE= ∠ACB
D.CE是∠ABC的平分线
D
6.如图,点O在直线AB上,射线OC平分∠BOD,
若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
C
7、图中共有几个角?
( )个角 ( )个角 ( )个角 ( )个角
3
6
10
45
课堂小结
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
同课章节目录
