2.5 全等三角形 第3课时 用“角边角”判定两个三角形全等 课件(共14张PPT) 初中数学湘教版八年级上册
文档属性
| 名称 | 2.5 全等三角形 第3课时 用“角边角”判定两个三角形全等 课件(共14张PPT) 初中数学湘教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 23:09:31 | ||
图片预览



文档简介
(共14张PPT)
2.5 全等三角形
第3课时 用“角边角”判定两个三角形全等
学习目标
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 掌握三角形全等的“ASA”条件;
3. 在探索三角形全等条件及其应用过程中,能够有条理地思考并进行简单的推理.
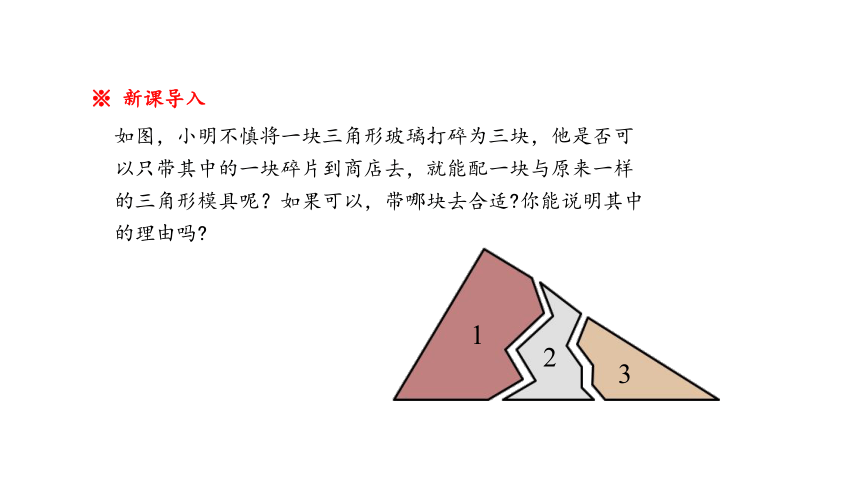
※ 新课导入
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适 你能说明其中的理由吗
3
2
1
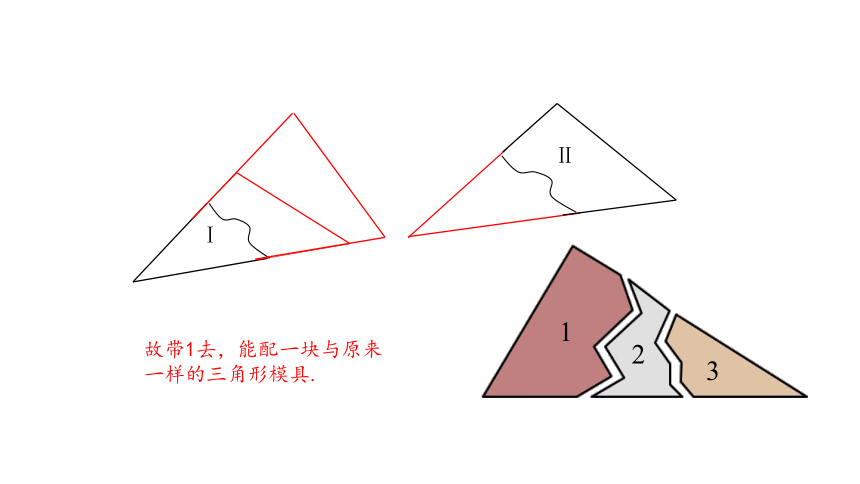
Ⅰ
Ⅱ
故带1去,能配一块与原来一样的三角形模具.
3
2
1
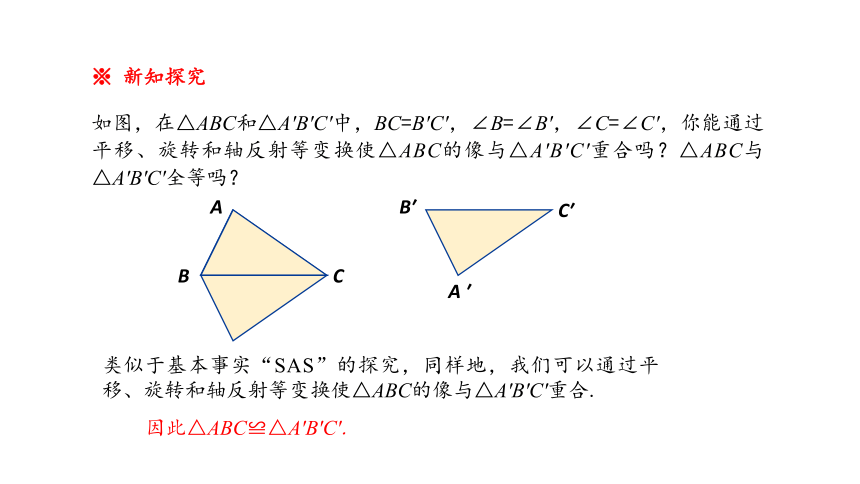
※ 新知探究
如图,在△ABC和△A′B′C′中,BC=B′C′,∠B=∠B′,∠C=∠C′,你能通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合吗?△ABC与△A′B′C′全等吗?
A
B
C
B′
C′
A ′
因此△ABC≌△A′B′C′.
类似于基本事实“SAS”的探究,同样地,我们可以通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合.
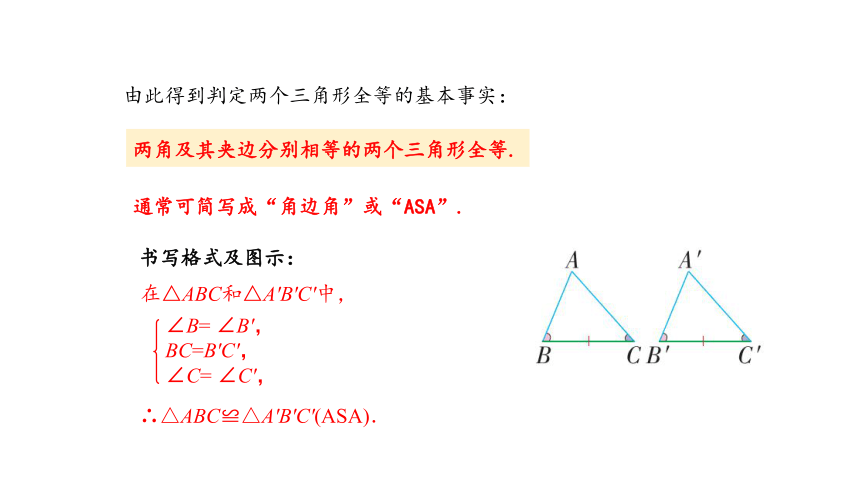
由此得到判定两个三角形全等的基本事实:
两角及其夹边分别相等的两个三角形全等.
通常可简写成“角边角”或“ASA”.
书写格式及图示:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
∠B= ∠B',
BC=B'C',
∠C= ∠C',
例3
已知:如图,点A,F,E,C在同一条直线上,AB∥DC,AB=CD,∠B=∠D.
求证:△ABE≌△CDF.
证明:∵AB∥DC,
∴∠A =∠C.
在△ABE 和△CDF 中,
∴△ABE≌△CDF (ASA).
∠A =∠C,
AB = CD,
∠B =∠D,
练一练
如图,已知AB∥DF,AC∥DE,BC=FE,且点B,E,C,F在一条直线上. 试说明:△ABC≌△DFE.
解:
因为AB∥DF且点B,E,C,F在一条直线上,
所以∠B=∠F.
因为AC∥DE,
所以∠ACB=∠DEF.
在△ABC和△DFE中,
∠B =∠F ,
BC =FE,
∠ACB =∠DEF ,
所以△ABC≌△DFE(ASA).
例4
如图,为测量河宽AB,小军从河岸的A点沿着与AB垂直的
A
B
E
C
D
在△AEB 和△CED 中,
∴△AEB≌△CED (ASA).
∴ AB = CD (全等三角形的对应边相等).
因此,CD 的长就是河的宽度.
∠A =∠C = 90°,
AE = CE,
∠AEB =∠CED (对顶角相等),
解:
方向走到C点,并在AC的中点 E 处立一根标杆,然后从C点沿着与AC垂直的方向走到D点,使D,E,B恰好在一条直线上. 于是小军说:“CD的长就是河的宽度.”你能说出这个道理吗?
练一练
已知:如图,在△ABC和△DCB中,∠ABC=∠DCB,∠ACB= ∠DBC,可证得△ABC≌△DCB.则判定两三角形全等的依据是 .
B
C
A
D
ASA
提示:BC是公共边.
※ 针对训练
1. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C. 求证:AD=AE.
A
D
B
C
O
E
证明:在△ACD 和△ABE 中,
∠A= ( ),
________ ( ),
∠C= ( ),
∴△ACD≌△ABE ( ).
∴AD=AE( ).
∠A
公共角
AB = AC
∠B
ASA
全等三角形的对应边相等
已知
已知
2.如图,已知AB=AE,∠1=∠2,∠B=∠E,求证:BC=ED.
A
B
E
C
D
1
2
证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠EAD=∠BAC.
∴△AED≌△ABC(ASA),
∴BC=ED(全等三角形的对应边相等)
在△AED和△ABC中,
∠E =∠B,
AE = AB,
∠EAD =∠BAC ,
※ 课堂小结
判定两个三角形全等的基本事实:
两角及其夹边分别相等的两个三角形全等.通常可简写成“角边角”或“ASA”.
数学语言:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
文字语言:
∠B= ∠B',
BC=B'C',
∠C= ∠C',
※ 课后练习
课本第80页练习第1-2题,
习题2.5第4题
2.5 全等三角形
第3课时 用“角边角”判定两个三角形全等
学习目标
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 掌握三角形全等的“ASA”条件;
3. 在探索三角形全等条件及其应用过程中,能够有条理地思考并进行简单的推理.
※ 新课导入
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适 你能说明其中的理由吗
3
2
1
Ⅰ
Ⅱ
故带1去,能配一块与原来一样的三角形模具.
3
2
1
※ 新知探究
如图,在△ABC和△A′B′C′中,BC=B′C′,∠B=∠B′,∠C=∠C′,你能通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合吗?△ABC与△A′B′C′全等吗?
A
B
C
B′
C′
A ′
因此△ABC≌△A′B′C′.
类似于基本事实“SAS”的探究,同样地,我们可以通过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合.
由此得到判定两个三角形全等的基本事实:
两角及其夹边分别相等的两个三角形全等.
通常可简写成“角边角”或“ASA”.
书写格式及图示:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
∠B= ∠B',
BC=B'C',
∠C= ∠C',
例3
已知:如图,点A,F,E,C在同一条直线上,AB∥DC,AB=CD,∠B=∠D.
求证:△ABE≌△CDF.
证明:∵AB∥DC,
∴∠A =∠C.
在△ABE 和△CDF 中,
∴△ABE≌△CDF (ASA).
∠A =∠C,
AB = CD,
∠B =∠D,
练一练
如图,已知AB∥DF,AC∥DE,BC=FE,且点B,E,C,F在一条直线上. 试说明:△ABC≌△DFE.
解:
因为AB∥DF且点B,E,C,F在一条直线上,
所以∠B=∠F.
因为AC∥DE,
所以∠ACB=∠DEF.
在△ABC和△DFE中,
∠B =∠F ,
BC =FE,
∠ACB =∠DEF ,
所以△ABC≌△DFE(ASA).
例4
如图,为测量河宽AB,小军从河岸的A点沿着与AB垂直的
A
B
E
C
D
在△AEB 和△CED 中,
∴△AEB≌△CED (ASA).
∴ AB = CD (全等三角形的对应边相等).
因此,CD 的长就是河的宽度.
∠A =∠C = 90°,
AE = CE,
∠AEB =∠CED (对顶角相等),
解:
方向走到C点,并在AC的中点 E 处立一根标杆,然后从C点沿着与AC垂直的方向走到D点,使D,E,B恰好在一条直线上. 于是小军说:“CD的长就是河的宽度.”你能说出这个道理吗?
练一练
已知:如图,在△ABC和△DCB中,∠ABC=∠DCB,∠ACB= ∠DBC,可证得△ABC≌△DCB.则判定两三角形全等的依据是 .
B
C
A
D
ASA
提示:BC是公共边.
※ 针对训练
1. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C. 求证:AD=AE.
A
D
B
C
O
E
证明:在△ACD 和△ABE 中,
∠A= ( ),
________ ( ),
∠C= ( ),
∴△ACD≌△ABE ( ).
∴AD=AE( ).
∠A
公共角
AB = AC
∠B
ASA
全等三角形的对应边相等
已知
已知
2.如图,已知AB=AE,∠1=∠2,∠B=∠E,求证:BC=ED.
A
B
E
C
D
1
2
证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即∠EAD=∠BAC.
∴△AED≌△ABC(ASA),
∴BC=ED(全等三角形的对应边相等)
在△AED和△ABC中,
∠E =∠B,
AE = AB,
∠EAD =∠BAC ,
※ 课堂小结
判定两个三角形全等的基本事实:
两角及其夹边分别相等的两个三角形全等.通常可简写成“角边角”或“ASA”.
数学语言:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
文字语言:
∠B= ∠B',
BC=B'C',
∠C= ∠C',
※ 课后练习
课本第80页练习第1-2题,
习题2.5第4题
同课章节目录
