2.5 全等三角形 第4课时 用“角角边”判定两个三角形全等 课件 (共15张PPT)初中数学湘教版八年级上册
文档属性
| 名称 | 2.5 全等三角形 第4课时 用“角角边”判定两个三角形全等 课件 (共15张PPT)初中数学湘教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 550.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 23:05:52 | ||
图片预览



文档简介
(共15张PPT)
2.5 全等三角形
第4课时 用“角角边”判定两个三角形全等
学习目标
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 掌握三角形全等的“AAS”条件;
3. 在探索三角形全等条件及其应用过程中,能够有条理地思考并进行简单的推理.
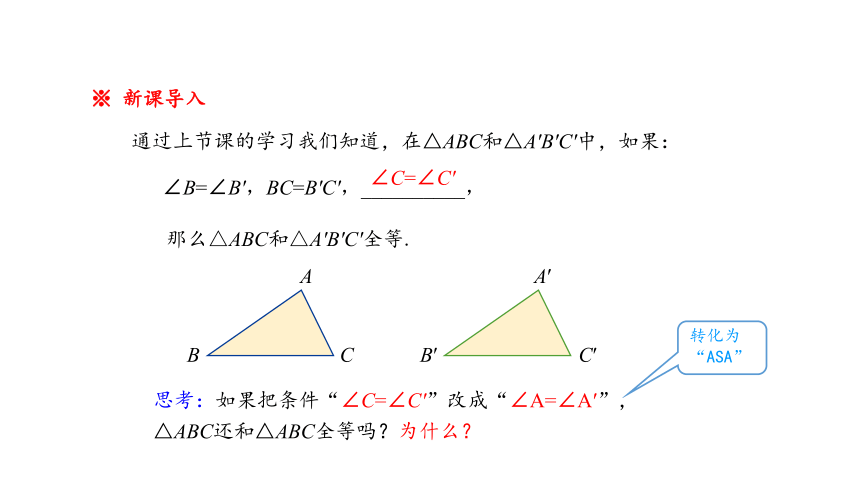
※ 新课导入
通过上节课的学习我们知道,在△ABC和△A′B′C′中,如果:
∠B=∠B′,BC=B′C′,__________,
那么△ABC和△A′B′C′全等.
A′
B′
C′
A
B
C
∠C=∠C′
思考:如果把条件“∠C=∠C′”改成“∠A=∠A′”,△ABC还和△ABC全等吗?为什么?
转化为“ASA”
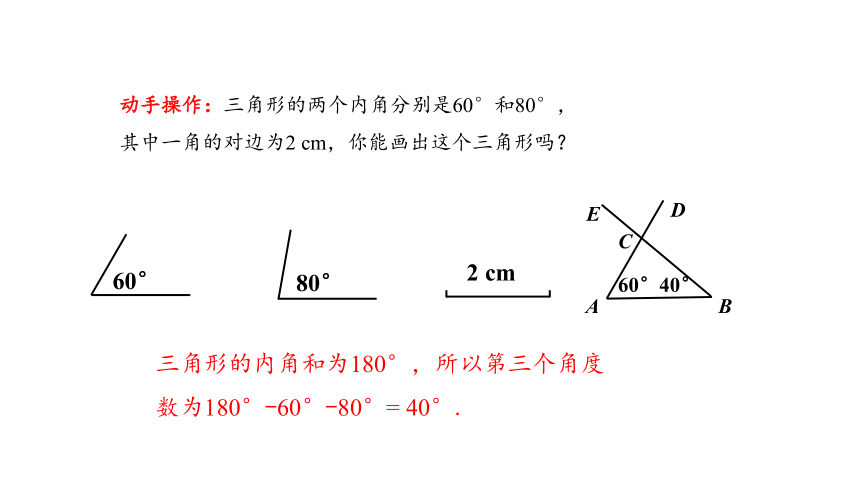
动手操作:三角形的两个内角分别是60°和80°,其中一角的对边为2 cm,你能画出这个三角形吗?
60°
80°
2 cm
60°
40°
A
B
E
D
C
三角形的内角和为180°,所以第三个角度数为180°-60°-80°= 40°.
※ 新知探究
如图,在△ABC和△A′B′C′中,如果∠A=∠A′,∠B=∠B′, BC=B′C′, 那么△ABC和△A′B′C′全等吗?
A′
B′
C′
A
B
C
根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件,从而可以证明△ABC≌△A'B'C'.
在△ABC 和△A′B′C′ 中,
∵∠A = ∠A′,∠B = ∠B′,
∴∠C =∠C′.
又∵ BC = B′C′,∠B =∠B′,
∴△ABC≌△A′B′C′ (ASA).
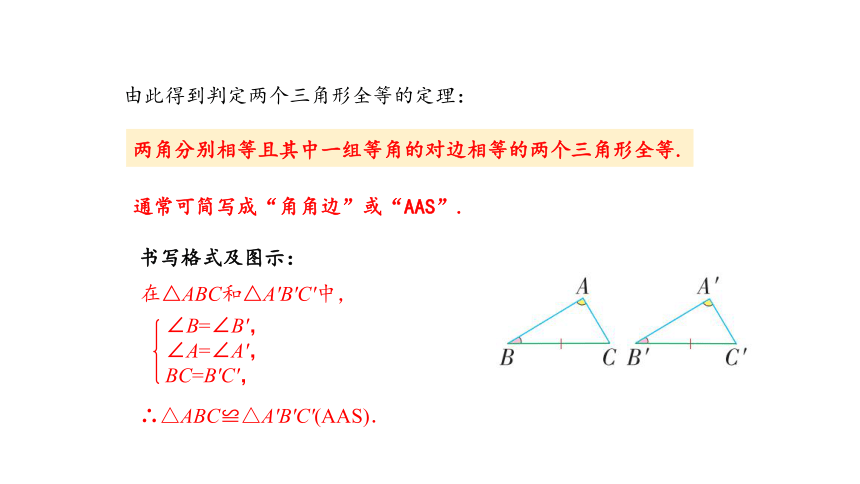
由此得到判定两个三角形全等的定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
通常可简写成“角角边”或“AAS”.
书写格式及图示:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
∠B=∠B',
∠A=∠A',
BC=B'C',
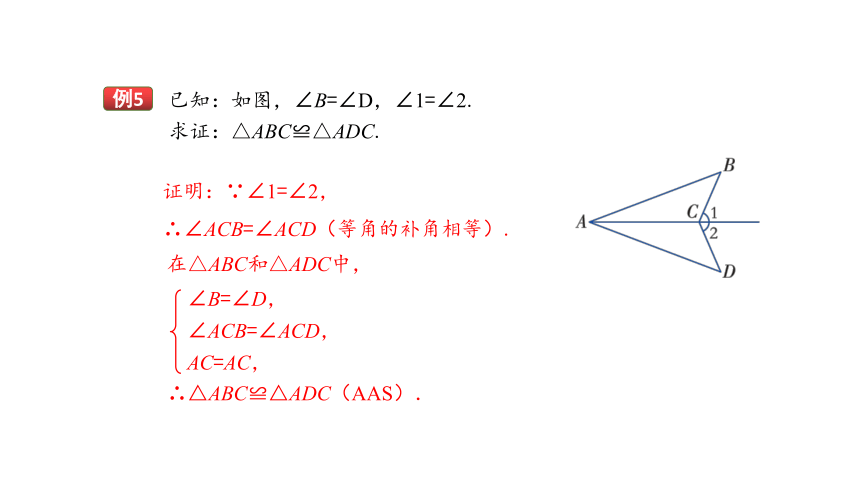
例5
已知:如图,∠B=∠D,∠1=∠2.
求证:△ABC≌△ADC.
证明:∵∠1=∠2,
∴∠ACB=∠ACD(等角的补角相等).
在△ABC和△ADC中,
∠B=∠D,
AC=AC,
∠ACB=∠ACD,
∴△ABC≌△ADC(AAS).
练一练
如图,已知∠A =∠D,AB = CD,可得△ABO≌_______,理由是_________.
A
B
C
D
O
△DCO
AAS
例6
已知:如图,点B,F,C,E在同一条直线上,AC∥FD,∠A=∠D,BF=EC. 求证:△ABC≌△DEF.
证明:∵AC∥FD,
∴∠ACB =∠DFE.
∵BF=EC,
∴BF+FC=EC+FC,
即BC=EF.
在△ABC 和△DEF 中,
∴△ABC≌△DEF (AAS).
∠A=∠D,
∠ACB=∠DFE,
BC=EF,
练一练
如图,点B,F,C,D在同一条直线上,AB=ED,AB∥ED,AC∥EF.求证:△ABC≌△EDF,BF=CD.
B
F
C
D
E
A
证明:∵ AB∥ED,AC∥EF,
∴∠B=∠D,∠ACB=∠EFD.
在△ABC 和△EDF 中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
AB=ED(已知),
∴△ABC≌△EDF (AAS).
∴BC=DF. ∴BF=CD.
※ 针对训练
1.已知:如图,AB⊥BC,AD⊥DC,∠1=∠2.
求证:AB=AD.
证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC 和△ADC 中,
∠1=∠2(已知),
∠B=∠D(已证),
AC=AC(公共边),
∴△ABC≌△ADC (AAS).
∴ AB=AD.
2.如图,∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
A
B
C
D
E
1
2
解:△ABC和△ADE全等.
∵∠1=∠2(已知),
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
∴ △ABC≌△ADE.
∠C=∠E(已知),
∠BAC=∠DAE(已证),
AB=AD(已知),
在△ABC和△ADC中,
3.如图,在△ABC中,∠BAC=90°,AB=AC,直线m经过点 A,BD⊥m,CE⊥m,垂足分别为点 D,E.
求证:(1) △BDA≌△AEC;(2) DE=BD+CE.
证明:(1)∵ BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°.
∴∠ABD+∠BAD=90°.
∵∠BAC=90°,
∴∠CAE+∠BAD=90°.
∴∠ABD=∠CAE.
在△BDA 和△AEC 中,
∴△BDA≌△AEC(AAS).
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴ BD=AE,AD=CE.
∴ DE=DA+AE=BD+CE.
(2)∵△BDA≌△AEC,
※ 课堂小结
判定两个三角形全等的定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.通常可简写成“角角边”或“AAS”.
数学语言:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
文字语言:
∠B= ∠B',
∠A= ∠A',
BC=B'C',
※ 课后练习
课本第82页练习第1-2题,
习题2.5第3,5题
2.5 全等三角形
第4课时 用“角角边”判定两个三角形全等
学习目标
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 掌握三角形全等的“AAS”条件;
3. 在探索三角形全等条件及其应用过程中,能够有条理地思考并进行简单的推理.
※ 新课导入
通过上节课的学习我们知道,在△ABC和△A′B′C′中,如果:
∠B=∠B′,BC=B′C′,__________,
那么△ABC和△A′B′C′全等.
A′
B′
C′
A
B
C
∠C=∠C′
思考:如果把条件“∠C=∠C′”改成“∠A=∠A′”,△ABC还和△ABC全等吗?为什么?
转化为“ASA”
动手操作:三角形的两个内角分别是60°和80°,其中一角的对边为2 cm,你能画出这个三角形吗?
60°
80°
2 cm
60°
40°
A
B
E
D
C
三角形的内角和为180°,所以第三个角度数为180°-60°-80°= 40°.
※ 新知探究
如图,在△ABC和△A′B′C′中,如果∠A=∠A′,∠B=∠B′, BC=B′C′, 那么△ABC和△A′B′C′全等吗?
A′
B′
C′
A
B
C
根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件,从而可以证明△ABC≌△A'B'C'.
在△ABC 和△A′B′C′ 中,
∵∠A = ∠A′,∠B = ∠B′,
∴∠C =∠C′.
又∵ BC = B′C′,∠B =∠B′,
∴△ABC≌△A′B′C′ (ASA).
由此得到判定两个三角形全等的定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
通常可简写成“角角边”或“AAS”.
书写格式及图示:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
∠B=∠B',
∠A=∠A',
BC=B'C',
例5
已知:如图,∠B=∠D,∠1=∠2.
求证:△ABC≌△ADC.
证明:∵∠1=∠2,
∴∠ACB=∠ACD(等角的补角相等).
在△ABC和△ADC中,
∠B=∠D,
AC=AC,
∠ACB=∠ACD,
∴△ABC≌△ADC(AAS).
练一练
如图,已知∠A =∠D,AB = CD,可得△ABO≌_______,理由是_________.
A
B
C
D
O
△DCO
AAS
例6
已知:如图,点B,F,C,E在同一条直线上,AC∥FD,∠A=∠D,BF=EC. 求证:△ABC≌△DEF.
证明:∵AC∥FD,
∴∠ACB =∠DFE.
∵BF=EC,
∴BF+FC=EC+FC,
即BC=EF.
在△ABC 和△DEF 中,
∴△ABC≌△DEF (AAS).
∠A=∠D,
∠ACB=∠DFE,
BC=EF,
练一练
如图,点B,F,C,D在同一条直线上,AB=ED,AB∥ED,AC∥EF.求证:△ABC≌△EDF,BF=CD.
B
F
C
D
E
A
证明:∵ AB∥ED,AC∥EF,
∴∠B=∠D,∠ACB=∠EFD.
在△ABC 和△EDF 中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
AB=ED(已知),
∴△ABC≌△EDF (AAS).
∴BC=DF. ∴BF=CD.
※ 针对训练
1.已知:如图,AB⊥BC,AD⊥DC,∠1=∠2.
求证:AB=AD.
证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC 和△ADC 中,
∠1=∠2(已知),
∠B=∠D(已证),
AC=AC(公共边),
∴△ABC≌△ADC (AAS).
∴ AB=AD.
2.如图,∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
A
B
C
D
E
1
2
解:△ABC和△ADE全等.
∵∠1=∠2(已知),
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
∴ △ABC≌△ADE.
∠C=∠E(已知),
∠BAC=∠DAE(已证),
AB=AD(已知),
在△ABC和△ADC中,
3.如图,在△ABC中,∠BAC=90°,AB=AC,直线m经过点 A,BD⊥m,CE⊥m,垂足分别为点 D,E.
求证:(1) △BDA≌△AEC;(2) DE=BD+CE.
证明:(1)∵ BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°.
∴∠ABD+∠BAD=90°.
∵∠BAC=90°,
∴∠CAE+∠BAD=90°.
∴∠ABD=∠CAE.
在△BDA 和△AEC 中,
∴△BDA≌△AEC(AAS).
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴ BD=AE,AD=CE.
∴ DE=DA+AE=BD+CE.
(2)∵△BDA≌△AEC,
※ 课堂小结
判定两个三角形全等的定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.通常可简写成“角角边”或“AAS”.
数学语言:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
文字语言:
∠B= ∠B',
∠A= ∠A',
BC=B'C',
※ 课后练习
课本第82页练习第1-2题,
习题2.5第3,5题
同课章节目录
