2.5 全等三角形 第5课时 用“边边边”判定两个三角形全等 课件 (共16张PPT)初中数学湘教版八年级上册
文档属性
| 名称 | 2.5 全等三角形 第5课时 用“边边边”判定两个三角形全等 课件 (共16张PPT)初中数学湘教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 23:13:23 | ||
图片预览



文档简介
(共16张PPT)
2.5 全等三角形
第5课时 用“边边边”判定两个三角形全等
学习目标
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 掌握三角形全等的“SSS”条件,了解三角形的稳定性;
3. 在探索三角形全等条件及其应用过程中,能够有条理地思考并进行简单的推理.
※ 新课导入
目前我们学习了几种三角形全等的判定方法?
SAS
ASA
AAS
思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定,如三角板中的两个三角形就不全等.
如果将上面的三个角换成三条边,结果又如何呢?
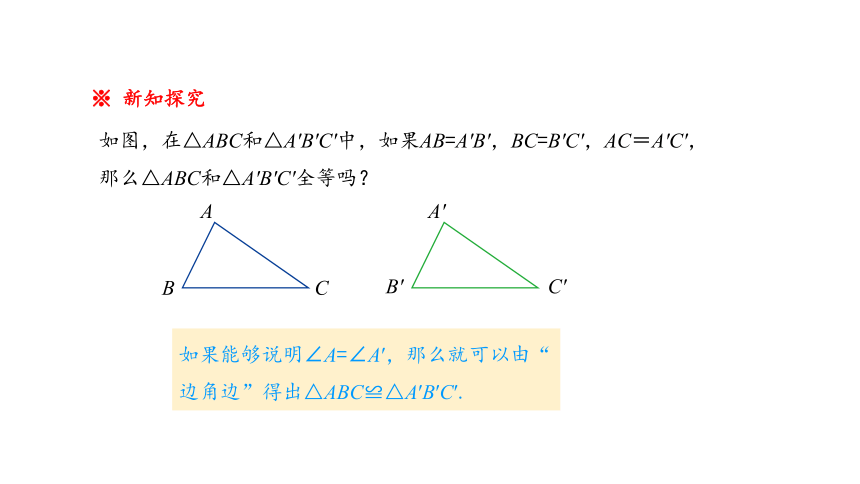
※ 新知探究
如图,在△ABC和△A′B′C′中,如果AB=A′B′,BC=B′C′,AC=A′C′,那么△ABC和△A′B′C′全等吗?
A
B
C
A′
B′
C′
如果能够说明∠A=∠A′,那么就可以由“边角边”得出△ABC≌△A′B′C′.
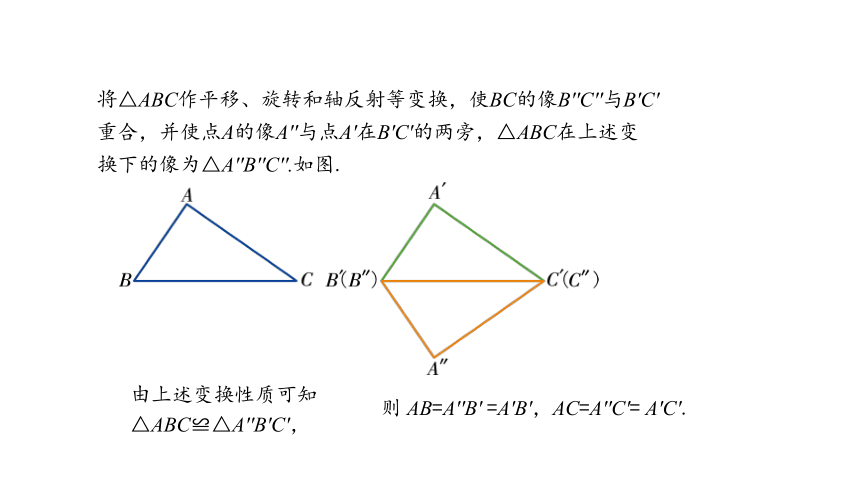
由上述变换性质可知△ABC≌△A′′B′C′,
则 AB=A′′B′ =A′B′,AC=A′′C′= A′C′.
将△ABC作平移、旋转和轴反射等变换,使BC的像B′′C′′与B′C′重合,并使点A的像A′′与点A′在B′C′的两旁,△ABC在上述变换下的像为△A′′B′′C′′.如图.
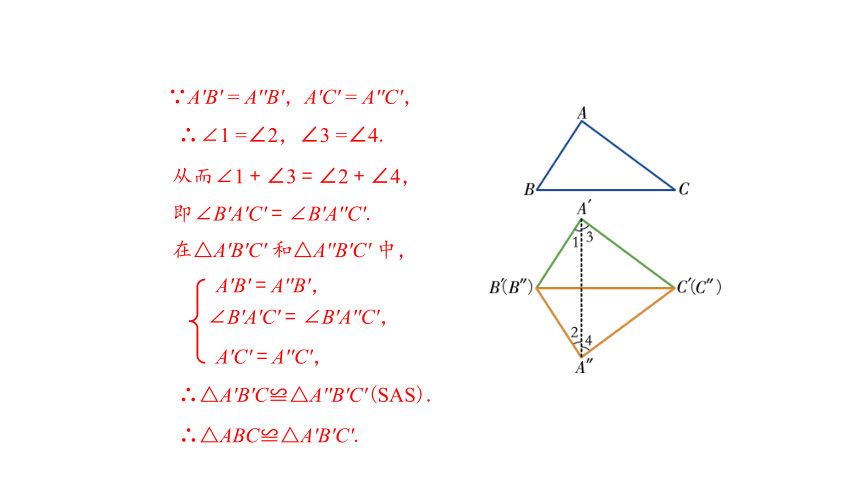
∴∠1 =∠2,∠3 =∠4.
从而∠1 + ∠3 = ∠2 + ∠4,
∵A′B′ = A′′B′,A′C′ = A′′C′,
即∠B′A′C′ = ∠B′A′′C′.
在△A′B′C′ 和△A′′B′C′ 中,
∴△A′B′C≌△A′′B′C′(SAS).
∴△ABC≌△A′B′C′.
A′B′ = A′′B′,
∠B′A′C′ = ∠B′A′′C′,
A′C′ = A′′C′,
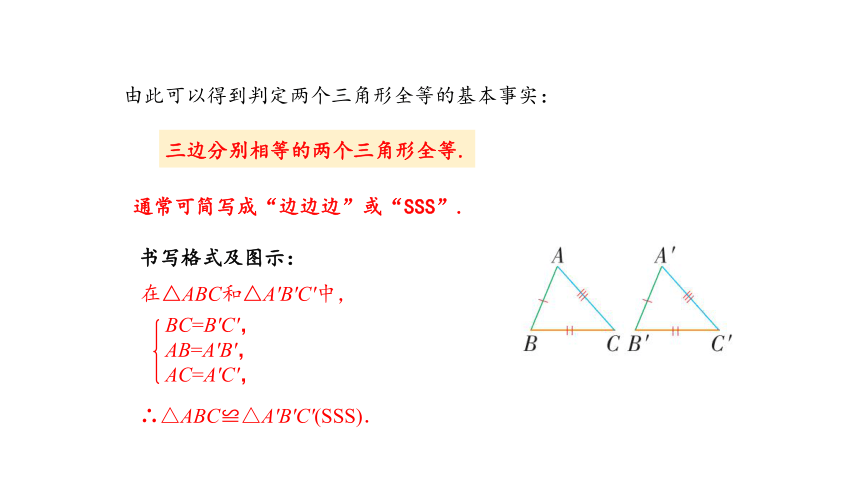
由此可以得到判定两个三角形全等的基本事实:
三边分别相等的两个三角形全等.
通常可简写成“边边边”或“SSS”.
书写格式及图示:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
BC=B'C',
AB=A'B',
AC=A'C',
例7
已知:如图,AB=CD,BC=DA.
求证:∠B=∠D.
证明:在△ABC和△CDA中,
AB = CD,
AC = CA(公共边),
BC = DA,
∴ △ABC≌△CDA(SSS).
∴ ∠B =∠D.
已知:如图,AC与BD相交于点O,且AB=DC,AC=DB.
求证:∠A=∠D.
证明:连接 BC.
在△ABC 和△DCB 中,
∴△ABC≌△DCB(SSS).
AB = DC,
BC = CB,
AC = DB,
∴∠A =∠D.
例8
动手做一做
准备几根硬纸条
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
(3)上面的现象说明了什么?
由“边边边”可知,只要三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
三角形的稳定性在生产和生活中有广泛的应用.
定位锁
人字梁屋顶
高压电铁塔
塔吊
※ 针对训练
1.要使四边形木架(用四根木条钉成)不变形,
至少要再钉上几根木条( )
A.1 B.2 C.3 D.4
A
具有稳定性
不具有稳定性
2.下列图形中哪些具有稳定性.
3. 如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;
③△ABD ≌△CDB;④ BA∥DC.
正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
C
O
A
B
C
D
4.已知:如图,在△ABC 中,AB=AC,点D,E在BC上,且AD=AE,BE=CD.
求证:△ABD≌△ACE.
证明:∵ BE = CD,
∴ BE - DE = CD - DE,
即 BD = CE.
在△ABD 和△ACE 中,
∴△ABD≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
※ 课堂小结
判定两个三角形全等的基本事实:
三边分别相等的两个三角形全等.通常可简写成“边边边”或“SSS”.
数学语言:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
文字语言:
BC=B'C',
AB=A'B',
AC=A'C',
三角形有稳定性
※ 课后练习
课本第84页练习第1-2题,
习题2.5第4题
2.5 全等三角形
第5课时 用“边边边”判定两个三角形全等
学习目标
1. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 掌握三角形全等的“SSS”条件,了解三角形的稳定性;
3. 在探索三角形全等条件及其应用过程中,能够有条理地思考并进行简单的推理.
※ 新课导入
目前我们学习了几种三角形全等的判定方法?
SAS
ASA
AAS
思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定,如三角板中的两个三角形就不全等.
如果将上面的三个角换成三条边,结果又如何呢?
※ 新知探究
如图,在△ABC和△A′B′C′中,如果AB=A′B′,BC=B′C′,AC=A′C′,那么△ABC和△A′B′C′全等吗?
A
B
C
A′
B′
C′
如果能够说明∠A=∠A′,那么就可以由“边角边”得出△ABC≌△A′B′C′.
由上述变换性质可知△ABC≌△A′′B′C′,
则 AB=A′′B′ =A′B′,AC=A′′C′= A′C′.
将△ABC作平移、旋转和轴反射等变换,使BC的像B′′C′′与B′C′重合,并使点A的像A′′与点A′在B′C′的两旁,△ABC在上述变换下的像为△A′′B′′C′′.如图.
∴∠1 =∠2,∠3 =∠4.
从而∠1 + ∠3 = ∠2 + ∠4,
∵A′B′ = A′′B′,A′C′ = A′′C′,
即∠B′A′C′ = ∠B′A′′C′.
在△A′B′C′ 和△A′′B′C′ 中,
∴△A′B′C≌△A′′B′C′(SAS).
∴△ABC≌△A′B′C′.
A′B′ = A′′B′,
∠B′A′C′ = ∠B′A′′C′,
A′C′ = A′′C′,
由此可以得到判定两个三角形全等的基本事实:
三边分别相等的两个三角形全等.
通常可简写成“边边边”或“SSS”.
书写格式及图示:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
BC=B'C',
AB=A'B',
AC=A'C',
例7
已知:如图,AB=CD,BC=DA.
求证:∠B=∠D.
证明:在△ABC和△CDA中,
AB = CD,
AC = CA(公共边),
BC = DA,
∴ △ABC≌△CDA(SSS).
∴ ∠B =∠D.
已知:如图,AC与BD相交于点O,且AB=DC,AC=DB.
求证:∠A=∠D.
证明:连接 BC.
在△ABC 和△DCB 中,
∴△ABC≌△DCB(SSS).
AB = DC,
BC = CB,
AC = DB,
∴∠A =∠D.
例8
动手做一做
准备几根硬纸条
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
(3)上面的现象说明了什么?
由“边边边”可知,只要三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
三角形的稳定性在生产和生活中有广泛的应用.
定位锁
人字梁屋顶
高压电铁塔
塔吊
※ 针对训练
1.要使四边形木架(用四根木条钉成)不变形,
至少要再钉上几根木条( )
A.1 B.2 C.3 D.4
A
具有稳定性
不具有稳定性
2.下列图形中哪些具有稳定性.
3. 如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;
③△ABD ≌△CDB;④ BA∥DC.
正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
C
O
A
B
C
D
4.已知:如图,在△ABC 中,AB=AC,点D,E在BC上,且AD=AE,BE=CD.
求证:△ABD≌△ACE.
证明:∵ BE = CD,
∴ BE - DE = CD - DE,
即 BD = CE.
在△ABD 和△ACE 中,
∴△ABD≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
※ 课堂小结
判定两个三角形全等的基本事实:
三边分别相等的两个三角形全等.通常可简写成“边边边”或“SSS”.
数学语言:
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
文字语言:
BC=B'C',
AB=A'B',
AC=A'C',
三角形有稳定性
※ 课后练习
课本第84页练习第1-2题,
习题2.5第4题
同课章节目录
