3.2 立方根 课件 (共15张PPT)初中数学湘教版八年级上册
文档属性
| 名称 | 3.2 立方根 课件 (共15张PPT)初中数学湘教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 309.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
3.2 立方根
学习目标
1. 了解立方根的概念,会用根号表示一个数的立方根;
2. 了解开立方与立方互为逆运算,能用立方根运算求某些数的立方根;
3. 能用计算器求一个数的立方根及其近似值.
※ 新课导入
如图,一个正方体的体积为8 cm3,它的棱长是多少?
由于23=8,因此体积为8 cm3的正方体,
它的棱长为2 cm.
※ 新知探究
立方根的概念
如果一个数b,使得b3=a,那么我们把b叫作a的一个立方根,也叫做三次方根.a的立方根记作 .
立方根的表示
a的立方根记作 ,读作:
立方根号a,或三次根号a.
例如,由于23=8,因此2是8的一个立方根,即 =2.
由于(-2)3=8,因此-2是-8的一个立方根,即 =-2.
a是被开方数,3是根指数.
练一练
根据立方根的意义填空:
因为( )3 = 0.125,所以 0.125 的立方根是( );
因为( )3 = 0,所以 0 的立方根是( );
0
0
0.5
0.5
因为( )3 = ,所以 的立方根是( ).
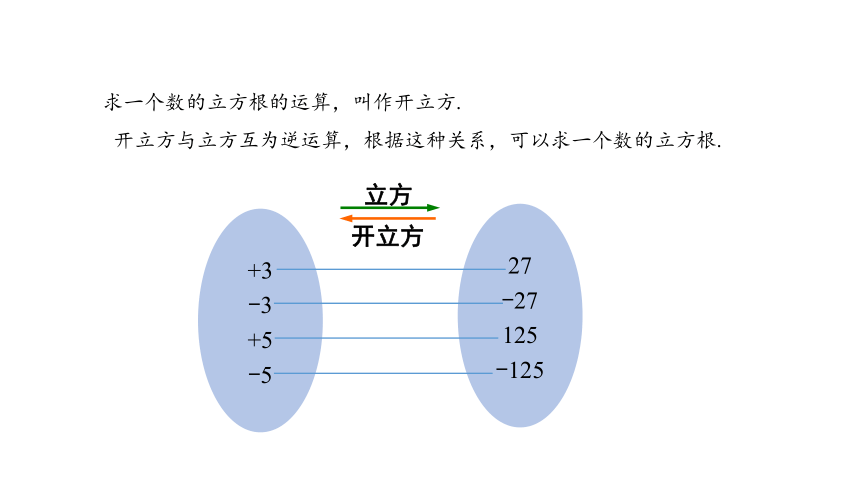
求一个数的立方根的运算,叫作开立方.
开立方与立方互为逆运算,根据这种关系,可以求一个数的立方根.
+3
-3
+5
-5
27
-27
125
-125
开立方
立方
例1
分别求下列各数的立方根:
1, ,0,-0.064.
解:
由于13=1,因此 =1;
由于03=0,因此 =0;
由于(-0.4)3=-0.064,因此 =-0.4.
由于 = ,因此 = ;
立方根的性质
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
练一练
分别求下列各数的立方根:
-27, ,0.216.
解:
由于(0.6)3=0.216,因此 =0.6.
由于(-3)3=-27,因此 =-3;
由于 = ,因此 = ;
例2
利用计算器可以求一个数的立方根或它的近似值.
用计算器求下列各数的立方根:
343,-1.331.
解:
按键:
显示:7
所以, =7.
3
4
3
=
2ndF
按键:
显示:-1.1
所以, =-1.1.
3
3
1
=
2ndF
(-)
1
.
键是第二功能键,相继按 键,意思是执行 上方所指 的功能运算.
2ndF
2ndF
例2
许多有理数的立方根都是无理数,我们可以用有理数来近似地表示它们.
用计算器求 的近似值(精确到0.001).
解:
按键:
显示:1.25992105
所以, ≈1.260.
2
=
2ndF
用计算器求 的近似值(精确到0.001).
练一练
≈2.289.
※ 针对训练
1.8的立方根为( )
A. B. C.2 D.±2
C
2.有下列四个说法:
①1的算术平方根是1;
② 的立方根是 ;
③-27没有立方根;
④互为相反数的两数的立方根互为相反数.
其中正确的是( )
A.①② B.①③ C.①④ D.②④
C
3.已知一个正数的两个平方根分别为3a-1和-5-a,则这个正数的立方根是多少?
解:
由题知3a-1+(-5-a)=0,解得a=3.
所以这个正数的两个平方根分别是8,-8.
所以这个正数是64.则这个正数的立方根为 =4.
4.求下列各式的值:
(4) 原式=-5+5-5-5=-10.
解:
※ 课堂小结
平方根与立方根的异同
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任何数
非负数
立方根是它本身的数有1, -1, 0;
平方根是它本身的数只有0.
※ 课后练习
课本第114页练习第1-3题,
习题3.2第1-4题
3.2 立方根
学习目标
1. 了解立方根的概念,会用根号表示一个数的立方根;
2. 了解开立方与立方互为逆运算,能用立方根运算求某些数的立方根;
3. 能用计算器求一个数的立方根及其近似值.
※ 新课导入
如图,一个正方体的体积为8 cm3,它的棱长是多少?
由于23=8,因此体积为8 cm3的正方体,
它的棱长为2 cm.
※ 新知探究
立方根的概念
如果一个数b,使得b3=a,那么我们把b叫作a的一个立方根,也叫做三次方根.a的立方根记作 .
立方根的表示
a的立方根记作 ,读作:
立方根号a,或三次根号a.
例如,由于23=8,因此2是8的一个立方根,即 =2.
由于(-2)3=8,因此-2是-8的一个立方根,即 =-2.
a是被开方数,3是根指数.
练一练
根据立方根的意义填空:
因为( )3 = 0.125,所以 0.125 的立方根是( );
因为( )3 = 0,所以 0 的立方根是( );
0
0
0.5
0.5
因为( )3 = ,所以 的立方根是( ).
求一个数的立方根的运算,叫作开立方.
开立方与立方互为逆运算,根据这种关系,可以求一个数的立方根.
+3
-3
+5
-5
27
-27
125
-125
开立方
立方
例1
分别求下列各数的立方根:
1, ,0,-0.064.
解:
由于13=1,因此 =1;
由于03=0,因此 =0;
由于(-0.4)3=-0.064,因此 =-0.4.
由于 = ,因此 = ;
立方根的性质
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
练一练
分别求下列各数的立方根:
-27, ,0.216.
解:
由于(0.6)3=0.216,因此 =0.6.
由于(-3)3=-27,因此 =-3;
由于 = ,因此 = ;
例2
利用计算器可以求一个数的立方根或它的近似值.
用计算器求下列各数的立方根:
343,-1.331.
解:
按键:
显示:7
所以, =7.
3
4
3
=
2ndF
按键:
显示:-1.1
所以, =-1.1.
3
3
1
=
2ndF
(-)
1
.
键是第二功能键,相继按 键,意思是执行 上方所指 的功能运算.
2ndF
2ndF
例2
许多有理数的立方根都是无理数,我们可以用有理数来近似地表示它们.
用计算器求 的近似值(精确到0.001).
解:
按键:
显示:1.25992105
所以, ≈1.260.
2
=
2ndF
用计算器求 的近似值(精确到0.001).
练一练
≈2.289.
※ 针对训练
1.8的立方根为( )
A. B. C.2 D.±2
C
2.有下列四个说法:
①1的算术平方根是1;
② 的立方根是 ;
③-27没有立方根;
④互为相反数的两数的立方根互为相反数.
其中正确的是( )
A.①② B.①③ C.①④ D.②④
C
3.已知一个正数的两个平方根分别为3a-1和-5-a,则这个正数的立方根是多少?
解:
由题知3a-1+(-5-a)=0,解得a=3.
所以这个正数的两个平方根分别是8,-8.
所以这个正数是64.则这个正数的立方根为 =4.
4.求下列各式的值:
(4) 原式=-5+5-5-5=-10.
解:
※ 课堂小结
平方根与立方根的异同
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
可以为任何数
非负数
立方根是它本身的数有1, -1, 0;
平方根是它本身的数只有0.
※ 课后练习
课本第114页练习第1-3题,
习题3.2第1-4题
同课章节目录
