2.6 用尺规作三角形 课件 (共15张PPT)初中数学湘教版八年级上册
文档属性
| 名称 | 2.6 用尺规作三角形 课件 (共15张PPT)初中数学湘教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 395.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 23:19:44 | ||
图片预览



文档简介
(共15张PPT)
2.6 用尺规作三角形
学习目标
1. 能利用尺规作角的平分线和已知角的等角;
2. 在分别给出两角及其夹边、两边及其夹角和三边的条件下,能够利用尺规作出三角形;
3. 了解作图方法的合理性.
※ 新课导入
1.尺规作图的工具是什么?
2.你已经学会用尺规作哪些图形?动手试一试.
直尺和圆规.
会作一条线段等于已知线段,会作线段的垂直平分线,会作已知直线的垂线……
根据三角形全等的判定条件,已知三边、两边及其夹角、两角及任何一边,都可以确定唯一的一个三角形.从而我们可以根据这些条件用尺规来作三角形.
※ 新知探究
·
·
·
·
·
·
c
b
a
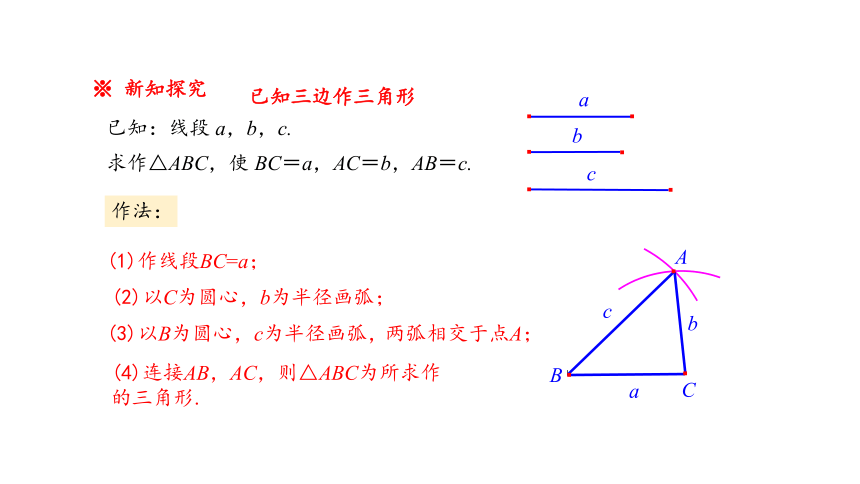
已知:线段 a,b,c.
求作△ABC,使 BC=a,AC=b,AB=c.
B
A
C
(1)作线段BC=a;
(2)以C为圆心,b为半径画弧;
(3)以B为圆心,c为半径画弧,
(4)连接AB,AC,则△ABC为所求作的三角形.
两弧相交于点A;
作法:
a
b
c
·
·
·
已知三边作三角形
已知底边及底边上的高线作等腰三角形
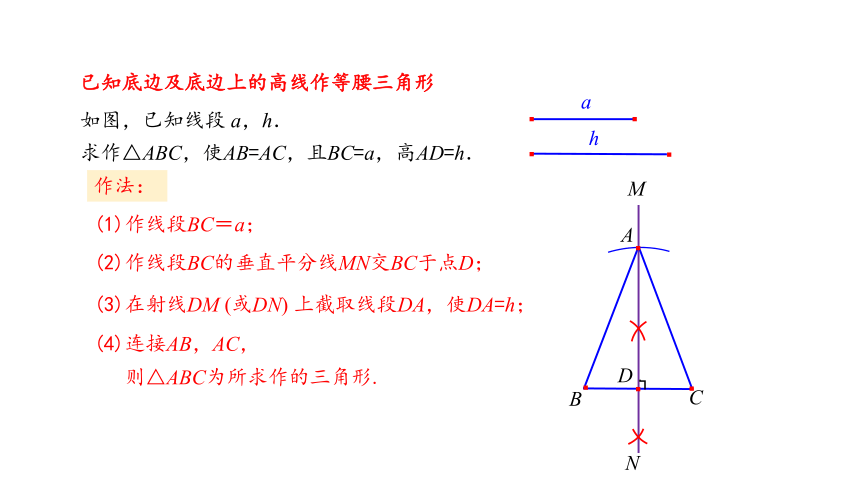
如图,已知线段 a,h.
求作△ABC,使AB=AC,且BC=a,高AD=h.
·
·
·
·
h
a
(1)作线段BC=a;
(2)作线段BC的垂直平分线MN交BC于点D;
(3)在射线DM (或DN) 上截取线段DA,使DA=h;
(4)连接AB,AC,
则△ABC为所求作的三角形.
作法:
A
D
C
B
N
M
·
·
·
·
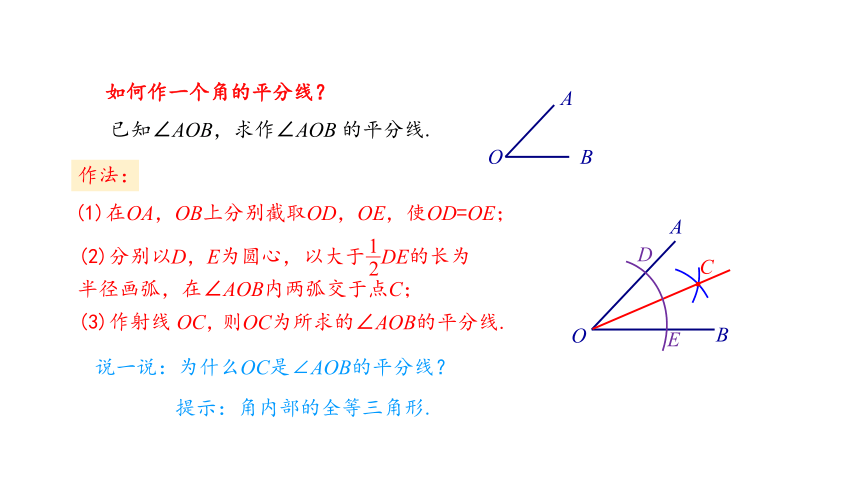
如何作一个角的平分线?
已知∠AOB,求作∠AOB 的平分线.
A
B
O
(2)分别以D,E为圆心,以大于 DE的长为半径画弧,在∠AOB内两弧交于点C;
A
B
O
(1)在OA,OB上分别截取OD,OE,使OD=OE;
1
2
(3)作射线 OC,
D
E
C
作法:
则OC为所求的∠AOB的平分线.
说一说:为什么OC是∠AOB的平分线?
提示:角内部的全等三角形.
·
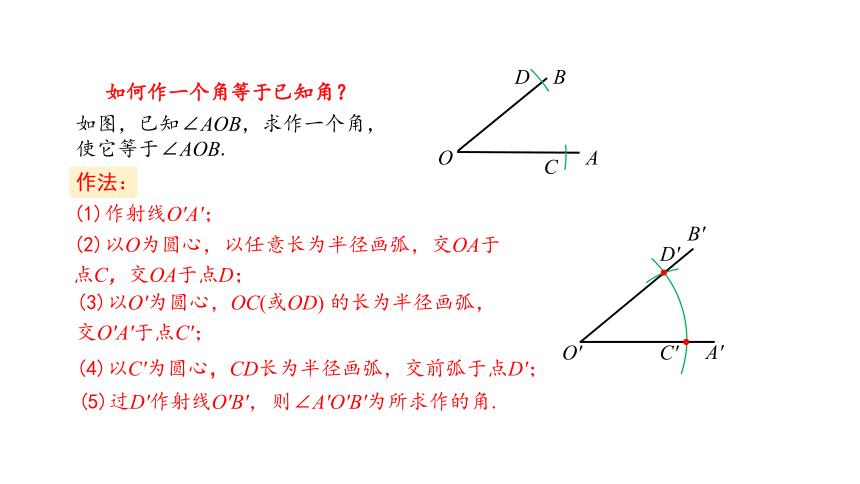
如何作一个角等于已知角?
O
B
A
如图,已知∠AOB,求作一个角,使它等于∠AOB.
D'
C'
B'
O'
A'
(1)作射线O'A';
(3)以O'为圆心,OC(或OD) 的长为半径画弧,交O'A'于点C';
(4)以C'为圆心,CD长为半径画弧,交前弧于点D';
则∠A'O'B'为所求作的角.
作法:
(5)过D'作射线O'B',
D
C
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OA于点D;
运用所学知识,请说一说:为什么∠A'O'B' 就是所求作的角?
解:由作图过程可知:
根据“SSS”可得△D'O'C'≌△DOC,
∴∠D'O'C'=∠DOC,
即∠A'O'B'=∠AOB.
O'C'=OC,O'D'=OD,D'C'=DC,
已知两边及其夹角作三角形
如图,已知∠α和线段a,c. 求作△ABC,使∠B=∠α,BC=a,BA=c.
(2)在射线BM,BN上分别截取BC=a,BA=c;
(3)连接AC,则△ABC为所求作的三角形.
(1)作∠MBN=∠α;
B
M
N
A
C
作法:
已知两角及其夹边作三角形
如图,已知∠α,∠β和线段a .
求作△ABC,使∠ABC=∠α,∠ACB=∠β,BC=a.
A
(1)作线段BC=a;
α
β
E
D
C
B
则△ABC为所求作的三角形.
作法:
(2)在BC的同旁,作∠DBC=∠α,∠ECB=∠β,BD与CE相交于点A.
※ 针对训练
1. 如图,△ABC 是三边均不相等的三角形,DE = BC,以 D,E 为两个顶点作位置不同的三角形,使所作的三角形与△ABC 全等,这样的三角形最多可以画 个.
A
B
C
D
E
4
O
a
分析:先作一个角等于已知角,即∠MBN =∠O,再在边BN上截取BC=a,以射线CB为一边,C为顶点,作∠PCB=2∠O,CP交BM于点A,△ABC即为所求作的三角形.
M
B
N
C
P
A
2. 如图,已知线段 a 及∠O,只用直尺和圆规,求作△ABC,使BC = a,∠B =∠O,∠C = 2∠B.
3. 如图,已知线段a,b,m,求作△ABC,使BC=2a,AC=b,且BC边上的中线AD=m.
解:作法:
(1)作△ADC,使AC=b,AD=m,
DC=a;
(2)作BD=a;
(3)连接AB,则△ABC即为
所求作的三角形,如图.
※ 课堂小结
常用作图语言
1.作∠……=∠……;
2.在……截取,使……=……;
3.以……顶点,以……为一边,作∠……=∠……;
4.作一条线段……=……;
5.连接……,或连接……交……于点……;
6.分别以……,……为圆心,以……,……为半径画弧,两弧交于……点.
用尺规作三角形的方法
1.已知两边及它们的夹角作三角形的方法
2.已知三边作三角形的方法
3.已知两角及它们的夹边作三角形的方法
※ 课后练习
课本第92页练习第1-2题,
习题2.5
2.6 用尺规作三角形
学习目标
1. 能利用尺规作角的平分线和已知角的等角;
2. 在分别给出两角及其夹边、两边及其夹角和三边的条件下,能够利用尺规作出三角形;
3. 了解作图方法的合理性.
※ 新课导入
1.尺规作图的工具是什么?
2.你已经学会用尺规作哪些图形?动手试一试.
直尺和圆规.
会作一条线段等于已知线段,会作线段的垂直平分线,会作已知直线的垂线……
根据三角形全等的判定条件,已知三边、两边及其夹角、两角及任何一边,都可以确定唯一的一个三角形.从而我们可以根据这些条件用尺规来作三角形.
※ 新知探究
·
·
·
·
·
·
c
b
a
已知:线段 a,b,c.
求作△ABC,使 BC=a,AC=b,AB=c.
B
A
C
(1)作线段BC=a;
(2)以C为圆心,b为半径画弧;
(3)以B为圆心,c为半径画弧,
(4)连接AB,AC,则△ABC为所求作的三角形.
两弧相交于点A;
作法:
a
b
c
·
·
·
已知三边作三角形
已知底边及底边上的高线作等腰三角形
如图,已知线段 a,h.
求作△ABC,使AB=AC,且BC=a,高AD=h.
·
·
·
·
h
a
(1)作线段BC=a;
(2)作线段BC的垂直平分线MN交BC于点D;
(3)在射线DM (或DN) 上截取线段DA,使DA=h;
(4)连接AB,AC,
则△ABC为所求作的三角形.
作法:
A
D
C
B
N
M
·
·
·
·
如何作一个角的平分线?
已知∠AOB,求作∠AOB 的平分线.
A
B
O
(2)分别以D,E为圆心,以大于 DE的长为半径画弧,在∠AOB内两弧交于点C;
A
B
O
(1)在OA,OB上分别截取OD,OE,使OD=OE;
1
2
(3)作射线 OC,
D
E
C
作法:
则OC为所求的∠AOB的平分线.
说一说:为什么OC是∠AOB的平分线?
提示:角内部的全等三角形.
·
如何作一个角等于已知角?
O
B
A
如图,已知∠AOB,求作一个角,使它等于∠AOB.
D'
C'
B'
O'
A'
(1)作射线O'A';
(3)以O'为圆心,OC(或OD) 的长为半径画弧,交O'A'于点C';
(4)以C'为圆心,CD长为半径画弧,交前弧于点D';
则∠A'O'B'为所求作的角.
作法:
(5)过D'作射线O'B',
D
C
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OA于点D;
运用所学知识,请说一说:为什么∠A'O'B' 就是所求作的角?
解:由作图过程可知:
根据“SSS”可得△D'O'C'≌△DOC,
∴∠D'O'C'=∠DOC,
即∠A'O'B'=∠AOB.
O'C'=OC,O'D'=OD,D'C'=DC,
已知两边及其夹角作三角形
如图,已知∠α和线段a,c. 求作△ABC,使∠B=∠α,BC=a,BA=c.
(2)在射线BM,BN上分别截取BC=a,BA=c;
(3)连接AC,则△ABC为所求作的三角形.
(1)作∠MBN=∠α;
B
M
N
A
C
作法:
已知两角及其夹边作三角形
如图,已知∠α,∠β和线段a .
求作△ABC,使∠ABC=∠α,∠ACB=∠β,BC=a.
A
(1)作线段BC=a;
α
β
E
D
C
B
则△ABC为所求作的三角形.
作法:
(2)在BC的同旁,作∠DBC=∠α,∠ECB=∠β,BD与CE相交于点A.
※ 针对训练
1. 如图,△ABC 是三边均不相等的三角形,DE = BC,以 D,E 为两个顶点作位置不同的三角形,使所作的三角形与△ABC 全等,这样的三角形最多可以画 个.
A
B
C
D
E
4
O
a
分析:先作一个角等于已知角,即∠MBN =∠O,再在边BN上截取BC=a,以射线CB为一边,C为顶点,作∠PCB=2∠O,CP交BM于点A,△ABC即为所求作的三角形.
M
B
N
C
P
A
2. 如图,已知线段 a 及∠O,只用直尺和圆规,求作△ABC,使BC = a,∠B =∠O,∠C = 2∠B.
3. 如图,已知线段a,b,m,求作△ABC,使BC=2a,AC=b,且BC边上的中线AD=m.
解:作法:
(1)作△ADC,使AC=b,AD=m,
DC=a;
(2)作BD=a;
(3)连接AB,则△ABC即为
所求作的三角形,如图.
※ 课堂小结
常用作图语言
1.作∠……=∠……;
2.在……截取,使……=……;
3.以……顶点,以……为一边,作∠……=∠……;
4.作一条线段……=……;
5.连接……,或连接……交……于点……;
6.分别以……,……为圆心,以……,……为半径画弧,两弧交于……点.
用尺规作三角形的方法
1.已知两边及它们的夹角作三角形的方法
2.已知三边作三角形的方法
3.已知两角及它们的夹边作三角形的方法
※ 课后练习
课本第92页练习第1-2题,
习题2.5
同课章节目录
