5.3 二次根式的加法和减法 课件 (共25张PPT)初中数学湘教版八年级上册
文档属性
| 名称 | 5.3 二次根式的加法和减法 课件 (共25张PPT)初中数学湘教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 23:23:46 | ||
图片预览








文档简介
(共25张PPT)
5.3 二次根式的加法和减法
第1课时 二次根式的加法和减法
学习目标
1. 理解二次根式的加、减运算法则;
2. 会进行简单的二次根式的加、减运算.
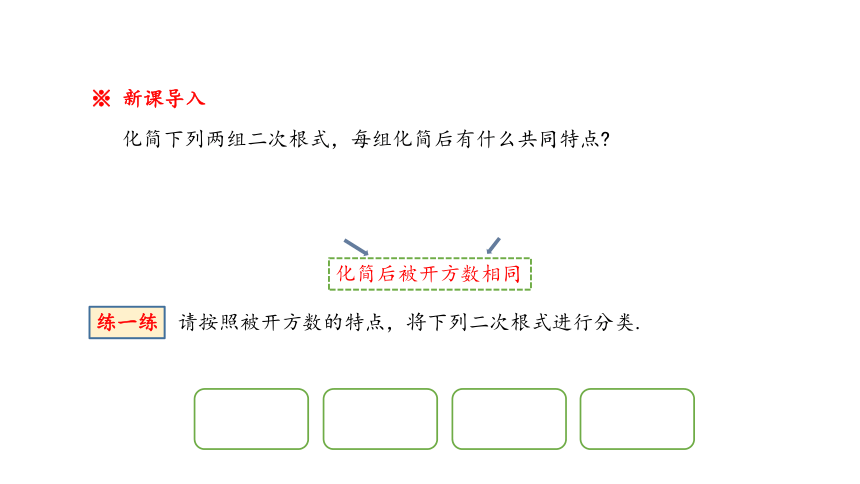
※ 新课导入
化简下列两组二次根式,每组化简后有什么共同特点
化简后被开方数相同
请按照被开方数的特点,将下列二次根式进行分类.
练一练
※ 新知探究
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得 2a + 3a = 5a.
当 a = 时,分别代入左右得 ;
当 a = 时,分别代入左右得 ;
......
你发现了什么?
a
2a + 3b
b
=
+
b
b
a
这两个二次根式可以合并吗?
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
因为 ,由前面知两者可以合并.
你又有什么发现吗
当a= ,b= 时,得2a+3b= .
计算:
如图是由面积分别为8和18的正方形ABCD和正方形CEGH拼成.求BE的长.
因为正方形ABCD和CEGH的边长分别为 和 ,所以BE的长度为 .
将二次根式化成最简,如果被开方数相同,则这样的二次根式可以合并.
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变. 如:
例1
计算:
解:
二次根式的加减与合并同类项类似.
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将同类二次根式进行合并.
(1) 化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2) 找——找出同类二次根式;
(3) 并——把同类二次根式合并.
“一化简二判断三合并”
练一练
计算:
解:
例2
下图是某土楼的平面剖面图,它是由两个相同圆心的圆构成. 已知大圆和小圆的面积分别为763.02 m2 和150.72 m2,求圆环的宽度d (π 取 3.14).
d
解:
设大圆和小圆的半径分别为 R,r,面积分别为 S1,S2,由 S1 = πR2,S2 = πr2,可得
则
答:圆环的宽度约为
※ 针对训练
1.二次根式 中,能与 合并的是( )
2.下列运算中错误的是 ( )
A.
B.
C.
D.
A
C
D. 与
A. 与
B. 与
C. 与
3.计算:
解:(1)
(2)
※ 课堂小结
二次根式的加减法
法则
注意
运算顺序
运算原理
一般地,进行二次根式的加减运算时,通常先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
5.3 二次根式的加法和减法
第2课时 二次根式的混合运算
学习目标
1. 掌握二次根式的混合运算的运算法则;
2.会应用乘法公式进行二次根式的计算;
3. 会运用二次根式的混合运算法则进行有关的运算.
※ 新课导入
甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 m,下底宽 m,高 m的梯形,这段路基长 500 m,那么这段路基的土石方 (路基的土石方即等于路基的体积)为多少立方米呢?
解:路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
从上面的解答过程可以看到,二次根式的混合运算是根据实数的运算律进行的.
答:这段路基的土石方为
※ 新知探究
计算:
例3
解:
二次根式相乘,与多项式的乘法类似,利用多项式的乘法可对某些二次根式的乘法进行化简.
计算:
利用平方差公式展开
利用完全平方公式展开
例4
多项式的乘法公式在二次根式的运算中仍然适用.
例5
计算:
解:
分母含二次根式的运算一般要先将分母变为有理数(式),然后按照二次根式的运算方法计算.
※ 针对训练
1.计算:
解:
解:
2.计算:
3.计算:
解:
4.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
※ 课堂小结
二次根式混合运算
乘法公式
运算顺序
二次根式的混合运算,先要弄清运算种类,再确定运算顺序:先乘除,再加减,有括号的要算括号内的,最后按照二次根式的相应的运算法则进行.
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
5.3 二次根式的加法和减法
第1课时 二次根式的加法和减法
学习目标
1. 理解二次根式的加、减运算法则;
2. 会进行简单的二次根式的加、减运算.
※ 新课导入
化简下列两组二次根式,每组化简后有什么共同特点
化简后被开方数相同
请按照被开方数的特点,将下列二次根式进行分类.
练一练
※ 新知探究
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得 2a + 3a = 5a.
当 a = 时,分别代入左右得 ;
当 a = 时,分别代入左右得 ;
......
你发现了什么?
a
2a + 3b
b
=
+
b
b
a
这两个二次根式可以合并吗?
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
因为 ,由前面知两者可以合并.
你又有什么发现吗
当a= ,b= 时,得2a+3b= .
计算:
如图是由面积分别为8和18的正方形ABCD和正方形CEGH拼成.求BE的长.
因为正方形ABCD和CEGH的边长分别为 和 ,所以BE的长度为 .
将二次根式化成最简,如果被开方数相同,则这样的二次根式可以合并.
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变. 如:
例1
计算:
解:
二次根式的加减与合并同类项类似.
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将同类二次根式进行合并.
(1) 化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2) 找——找出同类二次根式;
(3) 并——把同类二次根式合并.
“一化简二判断三合并”
练一练
计算:
解:
例2
下图是某土楼的平面剖面图,它是由两个相同圆心的圆构成. 已知大圆和小圆的面积分别为763.02 m2 和150.72 m2,求圆环的宽度d (π 取 3.14).
d
解:
设大圆和小圆的半径分别为 R,r,面积分别为 S1,S2,由 S1 = πR2,S2 = πr2,可得
则
答:圆环的宽度约为
※ 针对训练
1.二次根式 中,能与 合并的是( )
2.下列运算中错误的是 ( )
A.
B.
C.
D.
A
C
D. 与
A. 与
B. 与
C. 与
3.计算:
解:(1)
(2)
※ 课堂小结
二次根式的加减法
法则
注意
运算顺序
运算原理
一般地,进行二次根式的加减运算时,通常先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
5.3 二次根式的加法和减法
第2课时 二次根式的混合运算
学习目标
1. 掌握二次根式的混合运算的运算法则;
2.会应用乘法公式进行二次根式的计算;
3. 会运用二次根式的混合运算法则进行有关的运算.
※ 新课导入
甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 m,下底宽 m,高 m的梯形,这段路基长 500 m,那么这段路基的土石方 (路基的土石方即等于路基的体积)为多少立方米呢?
解:路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
从上面的解答过程可以看到,二次根式的混合运算是根据实数的运算律进行的.
答:这段路基的土石方为
※ 新知探究
计算:
例3
解:
二次根式相乘,与多项式的乘法类似,利用多项式的乘法可对某些二次根式的乘法进行化简.
计算:
利用平方差公式展开
利用完全平方公式展开
例4
多项式的乘法公式在二次根式的运算中仍然适用.
例5
计算:
解:
分母含二次根式的运算一般要先将分母变为有理数(式),然后按照二次根式的运算方法计算.
※ 针对训练
1.计算:
解:
解:
2.计算:
3.计算:
解:
4.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
※ 课堂小结
二次根式混合运算
乘法公式
运算顺序
二次根式的混合运算,先要弄清运算种类,再确定运算顺序:先乘除,再加减,有括号的要算括号内的,最后按照二次根式的相应的运算法则进行.
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
同课章节目录
