数学:2.1.3《函数的单调性》课件(新人教b必修1)
文档属性
| 名称 | 数学:2.1.3《函数的单调性》课件(新人教b必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 54.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:16:00 | ||
图片预览

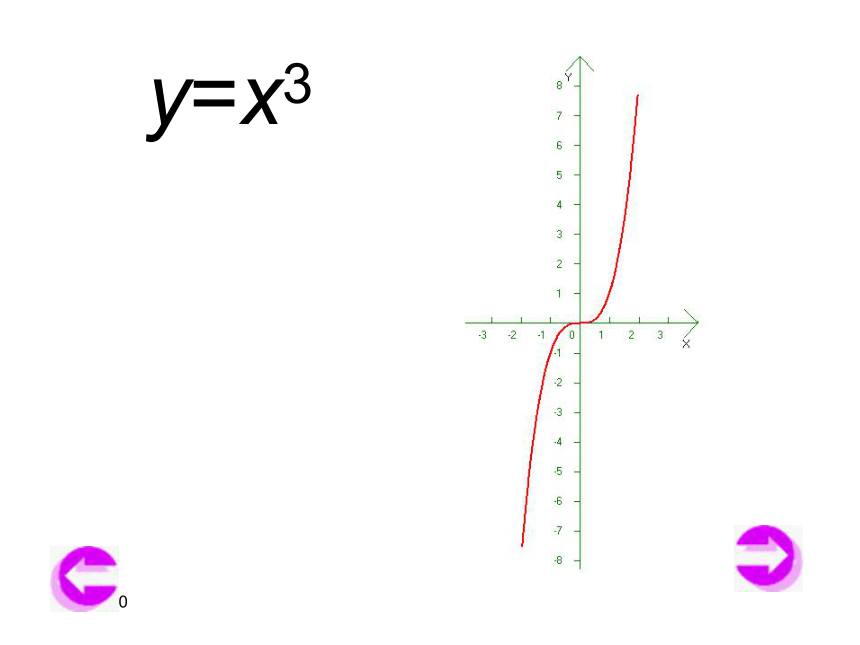

文档简介
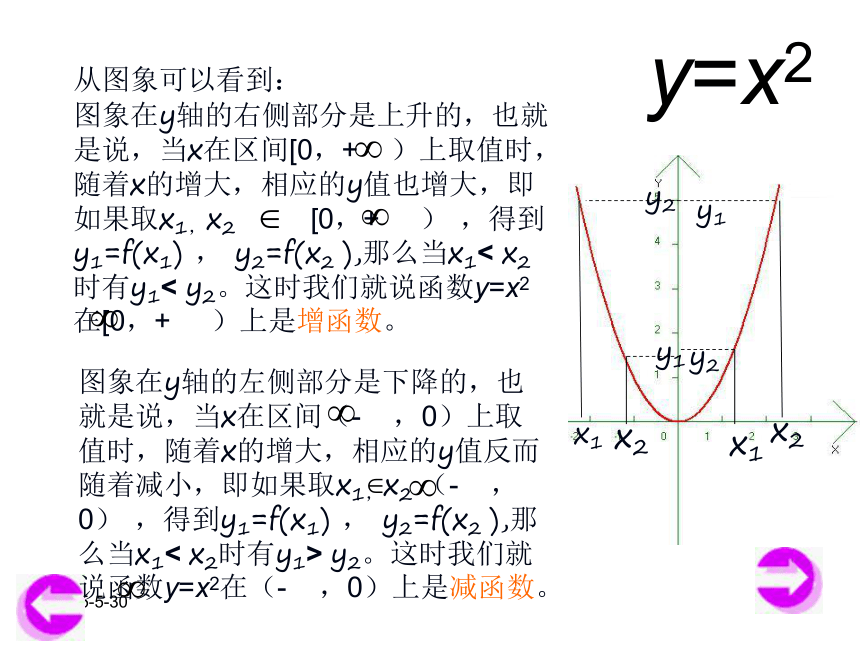
课件14张PPT。2019/3/13函数的单调性 2019/3/13y=x2 从图象可以看到:
图象在y轴的右侧部分是上升的,也就是说,当x在区间[0,+ )上取值时,随着x的增大,相应的y值也增大,即如果取x1,x2 [0,+ ) ,得到y1=f(x1) , y2=f(x2 ),那么当x1< x2时有y1< y2。这时我们就说函数y=x2在[0,+ )上是增函数。图象在y轴的左侧部分是下降的,也就是说,当x在区间(- ,0)上取值时,随着x的增大,相应的y值反而随着减小,即如果取x1,x2 (- ,0) ,得到y1=f(x1) , y2=f(x2 ),那么当x1< x2时有y1> y2。这时我们就说函数y=x2在(- ,0)上是减函数。
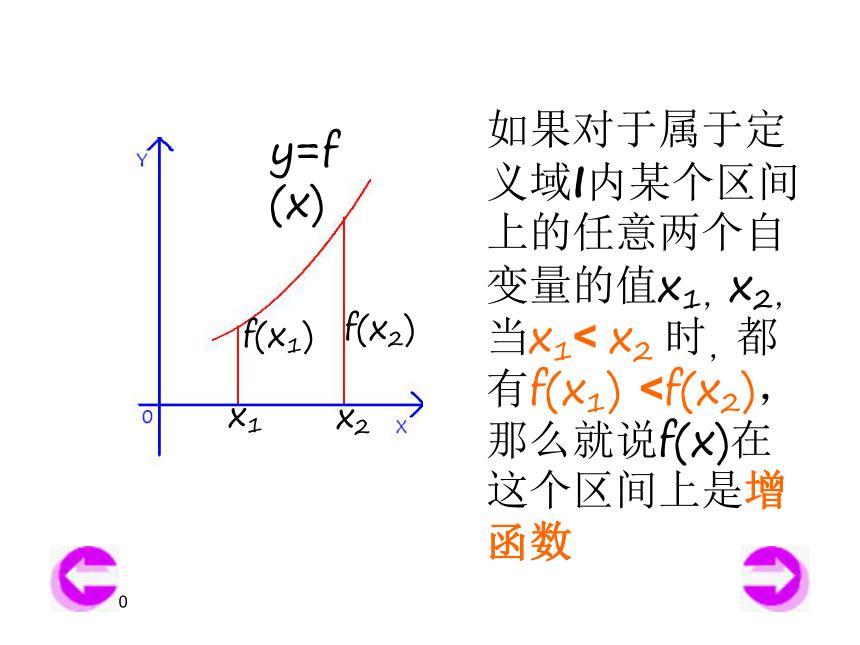
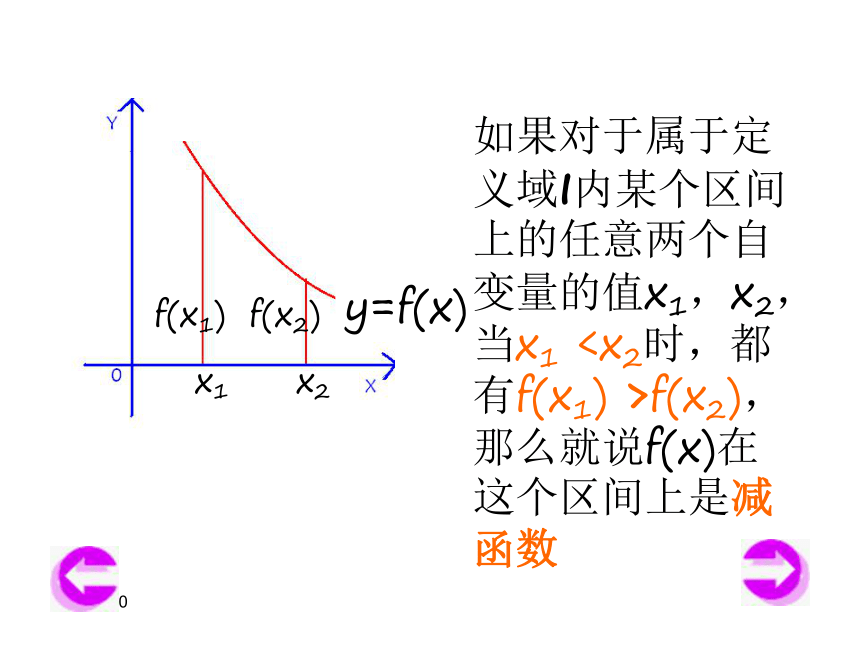
x1x2y1y2x2x1y2y12019/3/13y=x3 2019/3/13如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1< x2 时,都有f(x1)x1x2y=f(x)f(x1)f(x2)2019/3/13如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1 f(x2),那么就说f(x)在这个区间上是减函数
y=f(x)f(x1)f(x2)x1x22019/3/13如果函数y=f(x)在某个区间是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间中做y=f(x)的单调区间。在单调区间上增函数的图象是上升的,减函数的图象是下降的。
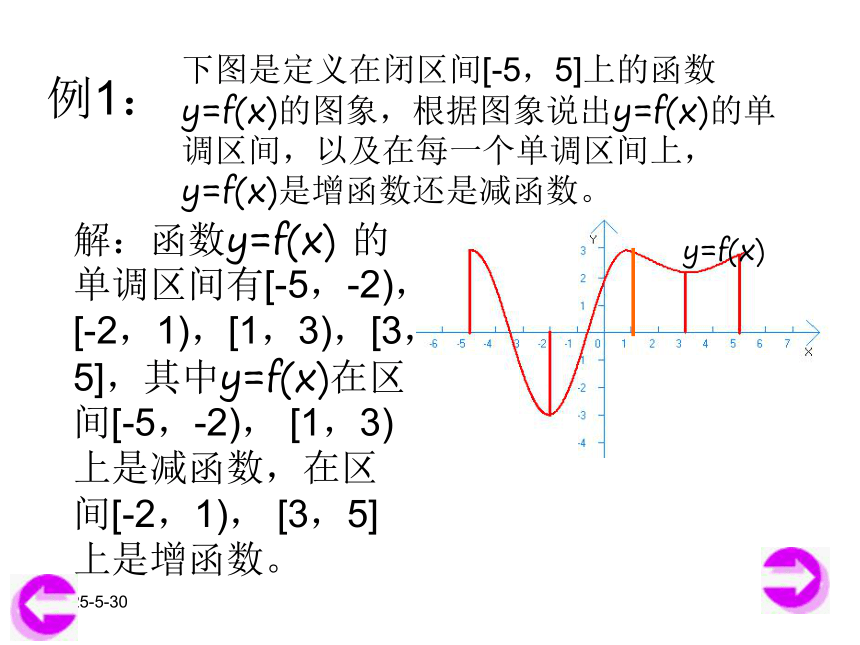
2019/3/13例1:下图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。解:函数y=f(x) 的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中y=f(x)在区间[-5,-2), [1,3)上是减函数,在区间[-2,1), [3,5]上是增函数。y=f(x)2019/3/13例2:证明函数f(x) =3x+2 在R上是增函数。证明:设x1,x2是R上的任意两个实数,且x1 < x2,则
f(x1) -f(x2) =(3x1+2)-(3x2+2)
=3(x1-x2)。
由x1 < x2,得x1 - x2 < 0,
于是 f(x1) -f(x2) < 0,
即 f(x1) < f(x2)
所以,f(x) =3x+2 在R上是增函数。2019/3/13证明函数单调性的步骤:1、设x1,x2属于给定区间2、作差f(x1) --f(x2)并判断符号3、根据函数的单调性定义肯定此命题成立2019/3/13例3:证明函数在 上是减函数。2019/3/13小结:1.有关单调性的定义;
2.关于单调区间的概念;
3.判断函数单调性的常用方法:定义法
2019/3/13练习1、如图,已知函数y=f(x),y=g(x)的图象(包括端点),根据图象说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数。y=f(x),y=g(x)2019/3/132、证明函数f(x)=-2x+1在R上是减函数。2019/3/13课本P46
AB作业
图象在y轴的右侧部分是上升的,也就是说,当x在区间[0,+ )上取值时,随着x的增大,相应的y值也增大,即如果取x1,x2 [0,+ ) ,得到y1=f(x1) , y2=f(x2 ),那么当x1< x2时有y1< y2。这时我们就说函数y=x2在[0,+ )上是增函数。图象在y轴的左侧部分是下降的,也就是说,当x在区间(- ,0)上取值时,随着x的增大,相应的y值反而随着减小,即如果取x1,x2 (- ,0) ,得到y1=f(x1) , y2=f(x2 ),那么当x1< x2时有y1> y2。这时我们就说函数y=x2在(- ,0)上是减函数。
x1x2y1y2x2x1y2y12019/3/13y=x3 2019/3/13如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1< x2 时,都有f(x1)
y=f(x)f(x1)f(x2)x1x22019/3/13如果函数y=f(x)在某个区间是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间中做y=f(x)的单调区间。在单调区间上增函数的图象是上升的,减函数的图象是下降的。
2019/3/13例1:下图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上, y=f(x)是增函数还是减函数。解:函数y=f(x) 的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中y=f(x)在区间[-5,-2), [1,3)上是减函数,在区间[-2,1), [3,5]上是增函数。y=f(x)2019/3/13例2:证明函数f(x) =3x+2 在R上是增函数。证明:设x1,x2是R上的任意两个实数,且x1 < x2,则
f(x1) -f(x2) =(3x1+2)-(3x2+2)
=3(x1-x2)。
由x1 < x2,得x1 - x2 < 0,
于是 f(x1) -f(x2) < 0,
即 f(x1) < f(x2)
所以,f(x) =3x+2 在R上是增函数。2019/3/13证明函数单调性的步骤:1、设x1,x2属于给定区间2、作差f(x1) --f(x2)并判断符号3、根据函数的单调性定义肯定此命题成立2019/3/13例3:证明函数在 上是减函数。2019/3/13小结:1.有关单调性的定义;
2.关于单调区间的概念;
3.判断函数单调性的常用方法:定义法
2019/3/13练习1、如图,已知函数y=f(x),y=g(x)的图象(包括端点),根据图象说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数。y=f(x),y=g(x)2019/3/132、证明函数f(x)=-2x+1在R上是减函数。2019/3/13课本P46
AB作业
