数学:3.1.3《导数的几何意义(2)》课件(新课标人教a版选修1-1)
文档属性
| 名称 | 数学:3.1.3《导数的几何意义(2)》课件(新课标人教a版选修1-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 64.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览


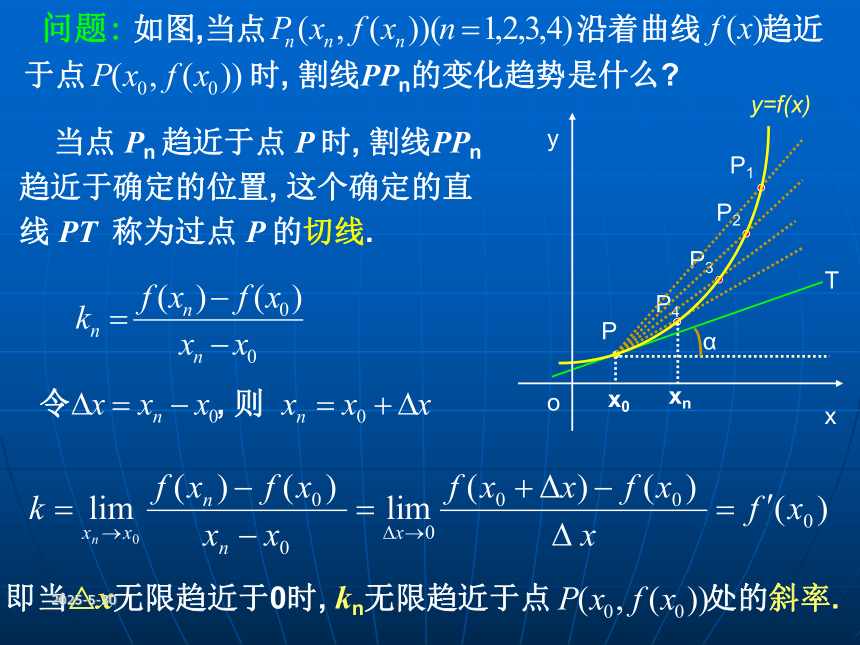

文档简介
课件9张PPT。2019/3/133.1.3 导数的几何意义2019/3/13函数 y = f (x) 在 x = x0 处的瞬时变化率称为函数 y = f (x) 在 x = x0 处的导数, 记作或 , 即2019/3/13 问题: 如图,当点 沿着曲线 趋近于点 时, 割线PPn的变化趋势是什么? 当点 Pn 趋近于点 P 时, 割线PPn趋近于确定的位置, 这个确定的直线 PT 称为过点 P 的切线.令 , 则即当△x无限趋近于0时, kn无限趋近于点 处的斜率.2019/3/13例1 已知 , 求曲线 在 处的切线的斜率. 分析:为求得过点(2,4)的切线的斜率, 可从经过点(2,4)的任意一条直线(割线)入手.解: 设 , 则割线PQ的斜率当 无限趋近于0时, 无限趋近于常数4, 即从而曲线 在点P(2,4)处的切线斜率为4.2019/3/13例2 如图, 它表示跳水运动中高度随时间变化的函数的图象. 根据图象, 请描述、比较曲线 在 附近的变化情况. 解:可用曲线 h(t) 在 t0 , t1 , t2 处的切线刻画曲线 h(t) 在上述三个时刻附近的变化情况.(1)当 t = t0 时, 曲线 h(t) 在 t0 处的切线 l0 平行于 x 轴.故在 t = t0 附近曲线比较平坦, 几乎没有升降.(2)当 t = t1 时, 曲线 h(t) 在 t1 处的切线 l1 的斜率 h’(t1) <0 .故在t = t1 附近曲线下降,即函数 h(t) 在 t = t1 附近单调递减.t4t3(3)当 t = t2 时, 曲线 h(t) 在 t2处的切线 l2 的斜率 h’(t2) <0 .故在 t = t2 附近曲线下降,即函数 h(t) 在t = t2 附近也单调递减.2019/3/13例2 . 根据图象, 请描述、比较曲线 在 附近的变化情况.解:可用曲线 h(t) 在 t0 , t1 , t2 处的切线刻画曲线 h(t) 在上述三个时刻附近的变化情况.(1)当 t = t0 时, 曲线 h(t) 在 t0 处的切线 l0 平行于 x 轴.故在 t = t0 附近曲线比较平坦, 几乎没有升降.(2)当 t = t1 时, 曲线 h(t) 在 t1 处的切线 l1 的斜率 h’(t1) <0 .故在t = t1 附近曲线下降,即函数 h(t) 在 t = t1 附近单调递减.(3)当 t = t2 时, 曲线 h(t) 在 t2处的切线 l2 的斜率 h’(t2) <0 .故在 t = t2 附近曲线下降,即函数 h(t) 在t = t2 附近也单调递减. 从图可以看出,直线 l1 的倾斜程度小于直线 l2 的倾斜程度,这说明 h(t) 曲线在 l1 附近比在 l2 附近下降得缓慢2019/3/13练习:2019/3/13A. 1条 B. 2条 C. 多于2条 D. 不能确定2019/3/13小结:作业:P87. 5
