数学:3.2.2《对数函数及其性质》课件(新人教b版必修1)
文档属性
| 名称 | 数学:3.2.2《对数函数及其性质》课件(新人教b版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 235.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 00:00:00 | ||
图片预览



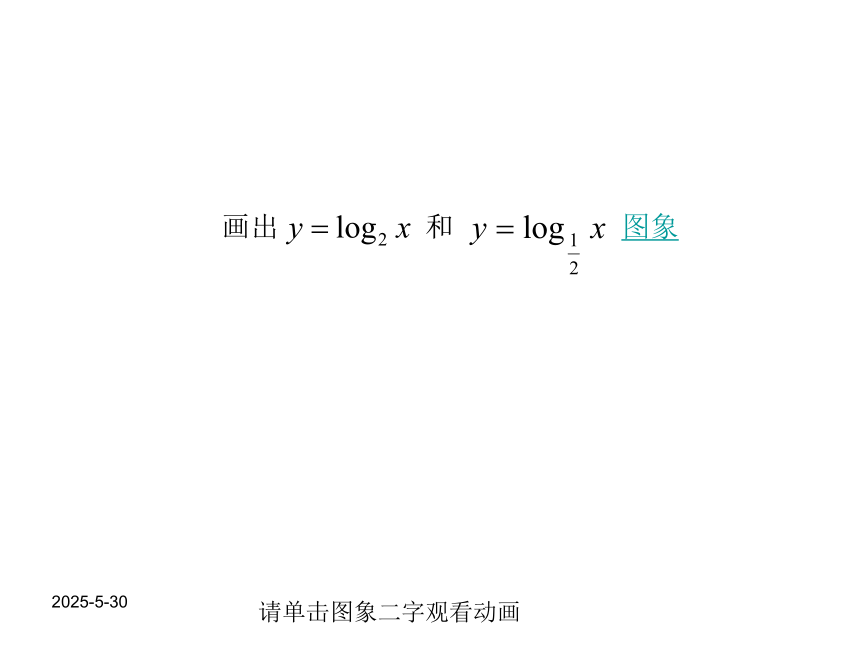
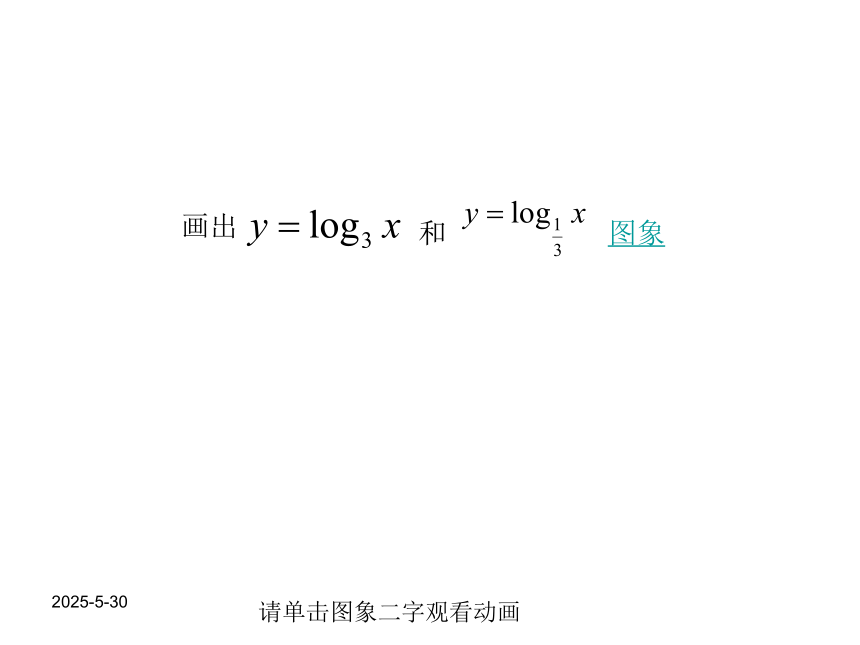
文档简介
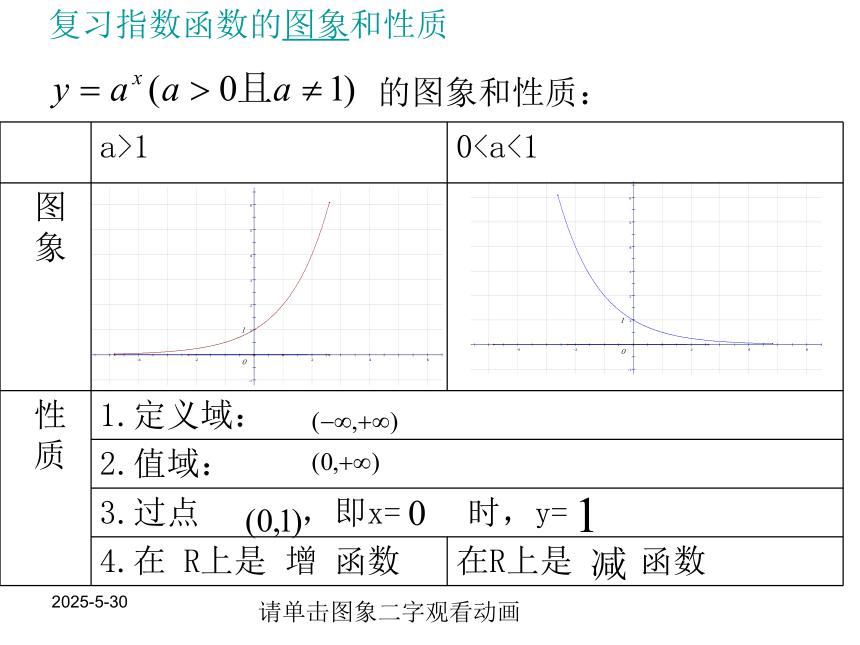
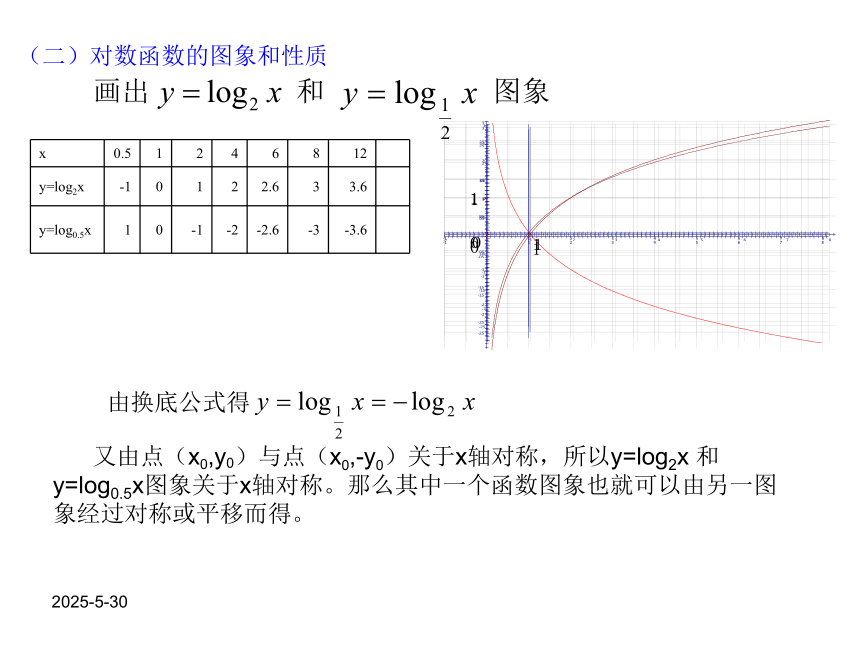
课件16张PPT。对数函数及其性质<一> 2019-3-13的图象和性质: 复习指数函数的图象和性质请单击图象二字观看动画2019-3-13一般地,如果 的b次幂等于N, 就是 那么数 b叫做以a为底 N的对数,记作: .a叫做对数的底数,N叫做真数。定义:复习对数的概念2019-3-13新课讲解: (一).对数函数的定义:函数 叫做对数函数; 其中x是自变量,函数的定义域是(0,+∞).注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如: (2)2019-3-13请单击图象二字观看动画2019-3-13(二)对数函数的图象和性质 又由点(x0,y0)与点(x0,-y0)关于x轴对称,所以y=log2x 和 y=log0.5x图象关于x轴对称。那么其中一个函数图象也就可以由另一图象经过对称或平移而得。2019-3-13请单击图象二字观看动画2019-3-13练习 1.画出函数 的图象,并且说明这两个函数的相同性质和不同性质.解:相同性质: y轴右方,都经过点(1,0),
这说明两函数的定义域
都是(0,+∞),且当
x=1,y=0.不同性质: 两图象都位于的图象是上升的曲线, 在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞)上是减函数.2019-3-13新授内容: 3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减图象演示请单击图象演示观看动画2019-3-13 . 类比指数函数图象和性质的研究研究对数函数的性质: 思考底数a是如何影响函数 y=logax的呢 ?
规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.2019-3-13例1求下列函数的定义域:(1) 讲解范例 分析:求函数定义域时应从哪些方面来考虑?
练习:求下列函数的定义域: 2019-3-13例2 讲解范例 解(1) 解(2) 比较下列各组数中两个值的大小: 考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,因为3.4<8.5,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,又因为1.8<2.7,于是 2019-3-13解(3) 当a>1时,以为函数y=logax在(0, +∞)上是增函数,且5.1<5.9,所以loga5.1 当0loga5.9(4)(5)分析(4):(5):2019-3-13练习:(教材P81练习3). (1) log106,log108(2) log0.56,log0.54(3) log2/30.5,log2/30.6(4) log1.51.3,log1.51.42019-3-13小结 :1.对数函数的定义:函数 叫做对数函数; 的定义域为 值域为 2019-3-13小结 :2.对数函数的图象和性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减2019-3-13
这说明两函数的定义域
都是(0,+∞),且当
x=1,y=0.不同性质: 两图象都位于的图象是上升的曲线, 在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞)上是减函数.2019-3-13新授内容: 3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减图象演示请单击图象演示观看动画2019-3-13 . 类比指数函数图象和性质的研究研究对数函数的性质: 思考底数a是如何影响函数 y=logax的呢 ?
规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.2019-3-13例1求下列函数的定义域:(1) 讲解范例 分析:求函数定义域时应从哪些方面来考虑?
练习:求下列函数的定义域: 2019-3-13例2 讲解范例 解(1) 解(2) 比较下列各组数中两个值的大小: 考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,因为3.4<8.5,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,又因为1.8<2.7,于是 2019-3-13解(3) 当a>1时,以为函数y=logax在(0, +∞)上是增函数,且5.1<5.9,所以loga5.1
(0,+∞)过点(1,0),即当x=1时,y=0 增减2019-3-13
