难点详解 沪科版八年级数学下册第20章 数据的初步分析 定向训练试题(名师精选)(含解析)
文档属性
| 名称 | 难点详解 沪科版八年级数学下册第20章 数据的初步分析 定向训练试题(名师精选)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 00:00:00 | ||
图片预览



文档简介
八年级数学下册第20章数据的初步分析定向训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、学校快餐店有12元,13元,14元三种价格的饭菜供师生选择(每人限购一份).下图是某月的销售情况统计图,则该校师生购买饭菜费用的平均数和众数是( )
A.12.95元,13元 B.13元,13元 C.13元,14元 D.12.95元,14元
2、在某中学举行的“筑梦路上”演讲比赛中,八年级5名参赛选手的成绩分别为:90,93,89,90,88.关于这5名选手的成绩,下列说法正确的是( )
A.平均数是89 B.众数是93
C.中位数是89 D.方差是2.8
3、某手机公司新推出了四款新型手机,公司为了了解各款手机的性能,随机抽取了每款手机各50台进行测试,以下是四款手机的性能得分(满分100分,分数越高,性能越好)的平均分和方差,则这四款新型手机中性能好且稳定的是( )
平均成绩(分) 95 98 96 98
方差 3 3 2 2
A. B. C. D.
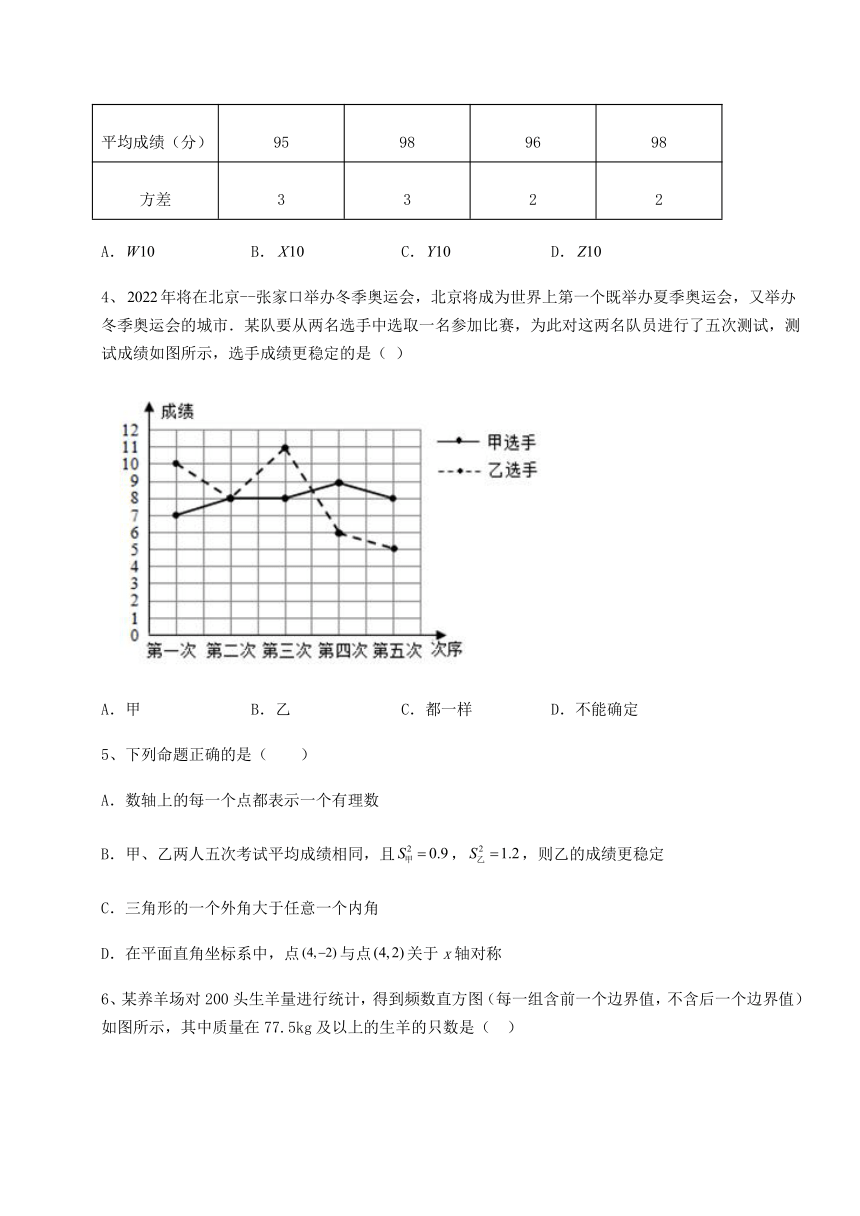
4、年将在北京--张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示,选手成绩更稳定的是( )
A.甲 B.乙 C.都一样 D.不能确定
5、下列命题正确的是( )
A.数轴上的每一个点都表示一个有理数
B.甲、乙两人五次考试平均成绩相同,且,,则乙的成绩更稳定
C.三角形的一个外角大于任意一个内角
D.在平面直角坐标系中,点与点关于x轴对称
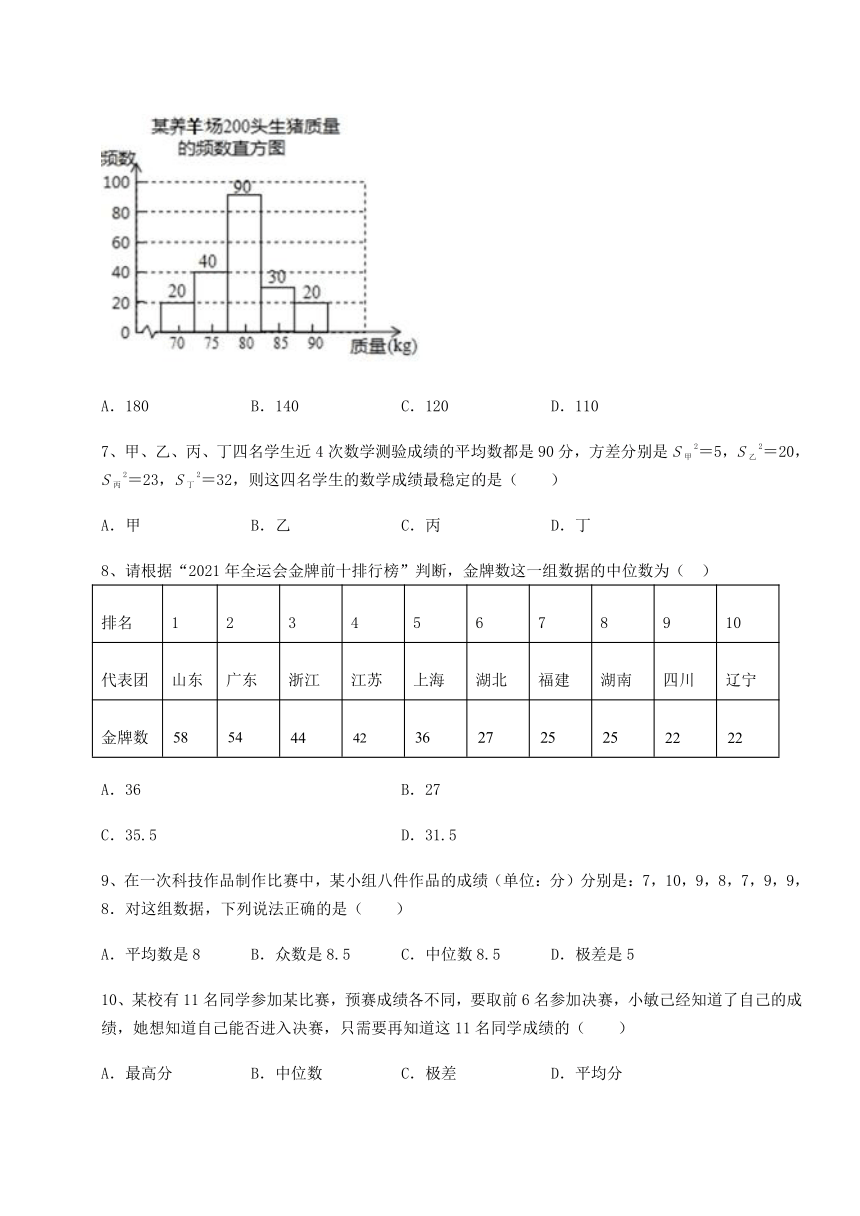
6、某养羊场对200头生羊量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )
A.180 B.140 C.120 D.110
7、甲、乙、丙、丁四名学生近4次数学测验成绩的平均数都是90分,方差分别是S甲2=5,S乙2=20,S丙2=23,S丁2=32,则这四名学生的数学成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
8、请根据“2021年全运会金牌前十排行榜”判断,金牌数这一组数据的中位数为( )
排名 1 2 3 4 5 6 7 8 9 10
代表团 山东 广东 浙江 江苏 上海 湖北 福建 湖南 四川 辽宁
金牌数
A.36 B.27
C.35.5 D.31.5
9、在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( )
A.平均数是8 B.众数是8.5 C.中位数8.5 D.极差是5
10、某校有11名同学参加某比赛,预赛成绩各不同,要取前6名参加决赛,小敏己经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这11名同学成绩的( )
A.最高分 B.中位数 C.极差 D.平均分
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、圆周率π≈3.141592653589793,数字5出现的频数是____.
2、为了庆祝中国共产党成立100周年,某校举行“歌唱祖国”班级合唱比赛,评委将从“舞台造型、合唱音准和进退场秩序”这三项进行打分,各项成绩均按百分制计算,然后再按舞台造型占40%,合唱音准占40%,进退场秩序占20%计算班级的综合成锁.七(1)班三项成绩依次是95分、90分、95分,则七(1)班的综合成绩为________.
3、有5个数据的平均数为24,另有15个数据的平均数是20,那么所有这20个数据的平均数是______.
4、甲、乙两同学5次数学考试的平均成绩都是132分,方差分别为S甲2=38,S乙2=10,则______ 同学的数学成绩更稳定.
5、一组数据的平均数是4,则这组数据的方差是_________.
三、解答题(5小题,每小题10分,共计50分)
1、为了让青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼.我校启动了“学生阳光体育短跑运动”,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补齐下面的表格:
次数 1 2 3 4 5
小明的成绩(秒) 13.3 13.4 13.3 ______ 13.3
小亮的成绩(秒) 13.2 ______ 13.1 13.5 13.3
(2)请写出小明的成绩的中位数和众数,小亮成绩的中位数;
(3)分别计算他们成绩的平均数和方差,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?
2、2021年4月13日,日本政府召开内阁会议正式决定,将福岛第一核电站超过100万公吨的核污水经过滤并稀释后排入大海,这一决定遭到包括福岛民众、日本渔民乃至国际社会的谴责和质疑.鉴于此次事件的恶劣影响,某校为了强化学生的环保意识,校团委在全校举办了“保护环境,人人有责”知识竞赛活动,初、高中根据初赛成绩,各选出5名选手组成初中代表队和高中代表队进行复赛,复赛成绩如图所示.
根据以上信息解答下列问题:
(1)高中代表队五名学生复赛成绩的中位数为 分;
(2)分别计算初中代表队、高中代表队学生复赛成绩的平均数;
(3)已知高中代表队学生复赛成绩的方差为20,请计算初中代表队学生复赛成绩的方差,并结合两队成绩的平均数和方差分析哪个队的复赛成绩较好.
3、某校为了增强学生的疫情防控意识,组织全校600名学生进行了疫情防控知识竞赛.从中随机抽取了名学生的竞赛成绩(满分100分,每名学生的成绩记为分),分成四组:组;组;组;组,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中信息,解答下列问题:
(1)求的值.
(2)补全频数分布直方图.
(3)若规定学生竞赛成绩为优秀,请估计全校竞赛成绩达到优秀的学生人数.
4、某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的满分均为100分,前6名选手的得分如下:
序号 1号 2号 3号 4号 5号
笔试成绩/分 85 92 84 90 84
面试成绩/分 90 88 86 90 80
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩.
(1)这6名选手笔试成绩的众数是 分.
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比.
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
5、随着经济的发展,我们身边的环境受到很大的影响,为了保护环境加强环保教育,某市实验中学组织500名学生参加义务收集废旧电池的活动,下面随机抽取50名学生对收集的废旧电池数量进行统计:
废旧电池数/节 3 4 5 6 8
人数/人 10 15 12 7 6
(1)这50名学生平均每人收集废旧电池多少节?
(2)这组废旧电池节数的中位数,众数分别是多少?
(3)根据统计发现,本次收集的各种废旧电池的数量比为:手机电池:7号电池:5号电池:1号电池=2:3:4:3,根据资料显示,各种电池1节能污染水的量之比为:手机电池:7号电池:5号电池:1号电池=6:1:2:3,且1节7号电池能使500吨的水受到污染,那么通过本次活动可减少受浸染的水多少吨?
-参考答案-
一、单选题
1、A
【分析】
可以设得总人数为x人,然后求得总钱数,再求平均数即可;在此题中购13元价格的饭菜的人最多,所以众数为13元.
【详解】
解:设本校共有师生x人,则买饭菜的费用是①12元:25%x×12=3x
②13元:55%x×13=7.15x,
③14元:20%x×14=2.8x
该校师生购买饭菜费用的平均数是(3x+7.15x+2.8x)÷x=12.95元.
购13元饭菜的人最多,所以众数为13元.
故选:A.
【点睛】
此题考查了众数与平均数的知识,属于简单题目.一组数据中出现次数最多的数据叫做众数.把所有数据相加后再除以数据的个数即得平均数.
2、D
【分析】
根据平均数、众数、中位数的定义以及方差公式计算即可得出答案.
【详解】
∵八年级5名参赛选手的成绩分别为:90,93,89,90,88,
从小到大排列为88,89,90,90,93,
∴平均数为,众数为90,中位数为90,
故选项A、B、C错误;
方差为,
故选项D正确.
故选:D.
【点睛】
本题考查平均数,众数和中位数,方差,掌握相关定义是解题的关键.
3、D
【分析】
先根据平均成绩选出,然后根据方差的意义求出
【详解】
解:根据平均数高,平均成绩好得出的性能好,
根据方差越小,数据波动越小可得出的性能好,
故选:D
【点睛】
本题主要考查了平均数和方差,熟练掌握平均数和方差的意义是解答本题的关键
4、A
【分析】
分别计算计算出甲乙选手的方差,根据方差越小数据越稳定解答即可.
【详解】
解:甲选手平均数为:,
乙选手平均数为:,
甲选手的方差为:,
乙选手的方差为:
∵可得出:,
则甲选手的成绩更稳定,
故选:A.
【点睛】
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
5、D
【分析】
根据数轴上的点与实数一一对应即可判断A;根据平均数相同的情形下,方差越小,成绩越稳定即可判断B;根据三角形的外角与内角的关系即可判断C;根据关于轴对称的点的坐标特征即可判断D
【详解】
A. 数轴上的每一个点都表示一个实数,故该选项不正确,不符合题意;
B. 甲、乙两人五次考试平均成绩相同,且,,则甲的成绩更稳定,故该选项不正确,不符合题意;
C. 三角形的一个外角不一定大于任意一个内角,故该选项不正确,不符合题意;
D. 在平面直角坐标系中,点与点关于x轴对称,故该选项正确,符合题意;
故选D
【点睛】
本题考查了实数与数轴,方差的意义,三角形的外角的性质,关于轴对称的点的坐标特征,掌握以上知识是解题的关键.
6、B
【分析】
根据题意和直方图中的数据可以求得质量在77.5kg及以上的生猪数,本题得以解决.
【详解】
解:由直方图可得,
质量在77.5kg及以上的生猪:90+30+20=140(头),
故选B.
【点睛】
本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
7、A
【分析】
根据方差的意义求解即可.
【详解】
解:∵S甲2=5,S乙2=20,S丙2=23,S丁2=32,
∴S甲2<S乙2<S丙2<S丁2,
∴这四名学生的数学成绩最稳定的是甲,
故选:A.
【点睛】
本题主要考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.
8、D
【分析】
根据中位数定义解答.将这组数据从小到大的顺序排列,第5、6个数的平均数为中位数.
【详解】
解:将这组数据从小到大的顺序排列处于中间位置的数即第5名和第6名的金牌数是36、27,
那么由中位数的定义可知,这组数据的中位数是.
故选D.
【点睛】
本题为统计题,考查中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
9、C
【分析】
计算这组数据的平均数、众数、中位数及极差即可作出判断.
【详解】
这组数据的平均数为:,众数为9,中位数为8.5,极差为10-7=3,故正确的是中位数为8.5.
故选:C
【点睛】
本题考查了反映一组数据平均数、众数、中位数、极差等知识,正确计算这些统计量是关键.
10、B
【分析】
由于共有11名同学参加某比赛,比赛取前6名参加决赛,根据中位数的意义分析即可.
【详解】
解:由于共有11个不同的成绩按从小到大排序后,中位数及中位数之后的共有6个数,
故只要知道自己的成绩和中位数就可以知道是否进入决赛了.
故选:B.
【点睛】
本题考查了中位数意义,解题的关键是正确掌握中位数的意义.
二、填空题
1、3
【分析】
从数5出现的次数即可得出答案.
【详解】
在中,5出现了3次,
∴数字5出现的频数是3.
故答案为:3.
【点睛】
本题考查频数的定义:一组数据中,某数据出现的次数,掌握频数的定义是解题的关键.
2、
【分析】
根据题意求这组数据的加权平均数即可.
【详解】
解:七(1)班的综合成绩为分
故答案为:
【点睛】
本题考查了求加权平均数,掌握加权平均数的计算是解题的关键,加权平均数计算公式为:,其中代表各数据的权.
3、21
【分析】
20个数据的总和为,故平均数为.
【详解】
解:
故答案为:.
【点睛】
本题考查了平均数.解题的关键是求出20个数据的总和.
4、乙
【分析】
根据平均数相同时,方差越小越稳定可以解答本题.
【详解】
解:∵甲、乙两同学5次数学考试的平均成绩都是132分,
方差分别为S甲2=38,S乙2=10,
∴S甲2S乙2,
∴乙同学的数学成绩更稳定,
故答案为:乙.
【点睛】
本题考查了方差,解题的关键是明确方差越小越稳定.
5、
【分析】
先根据平均数的定义求出x的值,再利用方差的定义列式计算即可.
【详解】
解:因为数据4,3,6,x的平均数是4,
可得:,
解得:x=3,
方差为:=,
故答案为:.
【点睛】
本题主要考查方差及算术平均数,解题的关键是掌握方差和平均数的定义.
三、解答题
1、(1)13.2,13.4;(2)小明:中位数13.3,众数13.3,小亮:中位数13.3;(3)小明的成绩比较稳定,因此对小亮的建议要加强稳定性训练,而小明应该加强爆发力训练,提高训练成绩.
【分析】
(1)从统计图中可得到每次百米训练的成绩,从而填入表格即可;
(2)根据中位数、众数的意义求出结果即可;
(3)计算两人的平均数、方差,再比较得出结论.
【详解】
解:(1)从统计图可知,小明第次的成绩为,小亮第次的成绩为,
故答案为:,;补全的表格如下:
次数 1 2 3 4 5
小明 13.3 13.4 13.3 13.2 13. 3
小亮 13.2 13.4 13.1 13.5 13.3
(2)小明次成绩的中位数是,众数为;
小亮次成绩的中位数是;
(3)小明
小亮
∴小明
小亮
∵小明小亮
∴小明小亮
∴小明的成绩比较稳定,因此对小亮的建议要加强稳定性训练,而小明应该加强爆发力训练,提高训练成绩.
【点睛】
本题考查折线统计图、加权平均数、中位数、众数以及方差的意义和计算方法,明确各个统计量的意义是正确解答的前提.
2、(1)95;(2)高中代表队的平均数为95分,初中代表队的平均数为90分;(3)初中代表队学生复赛成绩的方差为40,高中代表队成绩较好.
【分析】
(1)根据中位数的定义求解即可;
(2)根据平均数的定义求解即可;
(3)根据方差的定义求出初中代表队学生复赛成绩的方差,然后根据平均数和方差越小越稳定判断即可.
【详解】
解:(1)五个人的成绩从小到大排列为:90,90,95,100,100,
一共有5个数,第3个数为中位数,
∴中位数是95;
(2)高中代表队的平均数=(分),
初中代表队的平均数=(分);
(3)初中代表队学生复赛成绩的方差=,
∵,
∴高中代表队成绩较好.
【点睛】
此题考查了平均数,中位数和方差及其意义,解题的关键是熟练掌握平均数,中位数和方差的求解方法.
3、(1)50;(2)见解析;(3)180人
【分析】
(1)根据组的频数和所占的百分比,可以求得的值;
(2)根据(1)中的值和频数分布直方图中的数据,可以计算出组的频数,从而可以将频数分布直方图补充完整;
(3)根据直方图中的数据,可以计算出全校成绩达到优秀的人数.
【详解】
解:(1);
(2)组学生有:(人),
补全的频数分布直方图如图所示;
(3)(人),
答:估算全校成绩达到优秀的有180人.
【点睛】
本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确统计图的特点和中位数的含义,利用数形结合的思想解答.
4、(1)84;(2)笔试成绩和面试成绩各占的百分比是40%,60%;(3)2号:89.6分,3号:85.2分,4号:90分,5号:81.6分,6号:83分,综合成绩排序前两名人选是4号和2号
【分析】
(1)根据中位数和众数的定义即把这组数据从小到大排列,再找出最中间两个数的平均数就是中位数,再找出出现的次数最多的数即是众数;
(2)先设笔试成绩和面试成绩各占的百分百是x,y,根据题意列出方程组,求出x,y的值即可;
(3)根据笔试成绩和面试成绩各占的百分比,分别求出其余五名选手的综合成绩,即可得出答案.
【详解】
解:(1)把这组数据从小到大排列为,80,84,84,85,90,92,
84出现了2次,出现的次数最多,则这6名选手笔试成绩的众数是84分;
故答案为:84;
(2)设笔试成绩和面试成绩各占的百分比是x,y,根据题意得:
,
解得,
∴笔试成绩和面试成绩各占的百分比是40%,60%.
(3)2号选手的综合成绩是92×0.4+88×0.6=89.6(分),
3号选手的综合成绩是84×0.4+86×0.6=85.2(分),
4号选手的综合成绩是90×0.4+90×0.6=90(分),
5号选手的综合成绩是84×0.4+80×0.6=81.6(分),
6号选手的综合成绩是80×0.4+85×0.6=83(分).
∴综合成绩排序前两名人选是4号和2号.
【点睛】
本题考查了众数、二元一次方程组的实际应用,加权平均数等知识点,依据题意,正确建立方程求出题(2)中的笔试成绩和面试成绩各占的百分比是解题的关键.
5、(1)4.8节;(2)众数为4个,中位数为4.5节;(3)本次活动可减少受浸染的水3200000吨.
【分析】
(1)求出50名学生收集废旧电池的总数,再求平均数即可;
(2)从统计表格即可求得众数为5,然后按从大到小给所有数据排序,求出中位数即可;
(3)先求出这些电池可污染的水的数量即可解决问题.
【详解】
解:(1)50名学生平均每人收集废旧电池的节数=(10×3+15×4+12×5+7×6+6×8)÷50=4.8(节);
(2)从统计表格得,众数为4节;
由于收集3节和4节电池的人数有25个人,收集5节的人有12人,所以中位数=(4+5)÷2=4.5(节);
(3)样本中电池总数4.8×50=240,
由于本次收集的各种电池的数量比为:手机电池:7号电池:5号电池:1号电池=2:3:4:3,
故可得出手机电池、7号电池、5号电池、1号电池与总数的比值分别为:
,,,,即,,,,
由于各种电池1节能污染水的量的比为:手机电池:7号电池:5号电池:1号电池=6:1:2:3,且1节7号电池能使500吨的水受到污染,故可得手机电池、5号电池、1号电池一节分别能污染水的吨数为500×6,500×2,500×3,
故在50名学生收集的废电池可少受污染水的吨数为
=320000(吨)
320000÷50×500=3200000吨,
答:本次活动可减少受浸染的水3200000吨.
【点睛】
本题考查了从统计图中获取信息的能力;对平均数、中位数和众数等概念的掌握程度.同时通过此题倡导学生参加义务收集废旧电池活动中来.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、学校快餐店有12元,13元,14元三种价格的饭菜供师生选择(每人限购一份).下图是某月的销售情况统计图,则该校师生购买饭菜费用的平均数和众数是( )
A.12.95元,13元 B.13元,13元 C.13元,14元 D.12.95元,14元
2、在某中学举行的“筑梦路上”演讲比赛中,八年级5名参赛选手的成绩分别为:90,93,89,90,88.关于这5名选手的成绩,下列说法正确的是( )
A.平均数是89 B.众数是93
C.中位数是89 D.方差是2.8
3、某手机公司新推出了四款新型手机,公司为了了解各款手机的性能,随机抽取了每款手机各50台进行测试,以下是四款手机的性能得分(满分100分,分数越高,性能越好)的平均分和方差,则这四款新型手机中性能好且稳定的是( )
平均成绩(分) 95 98 96 98
方差 3 3 2 2
A. B. C. D.
4、年将在北京--张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示,选手成绩更稳定的是( )
A.甲 B.乙 C.都一样 D.不能确定
5、下列命题正确的是( )
A.数轴上的每一个点都表示一个有理数
B.甲、乙两人五次考试平均成绩相同,且,,则乙的成绩更稳定
C.三角形的一个外角大于任意一个内角
D.在平面直角坐标系中,点与点关于x轴对称
6、某养羊场对200头生羊量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )
A.180 B.140 C.120 D.110
7、甲、乙、丙、丁四名学生近4次数学测验成绩的平均数都是90分,方差分别是S甲2=5,S乙2=20,S丙2=23,S丁2=32,则这四名学生的数学成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
8、请根据“2021年全运会金牌前十排行榜”判断,金牌数这一组数据的中位数为( )
排名 1 2 3 4 5 6 7 8 9 10
代表团 山东 广东 浙江 江苏 上海 湖北 福建 湖南 四川 辽宁
金牌数
A.36 B.27
C.35.5 D.31.5
9、在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( )
A.平均数是8 B.众数是8.5 C.中位数8.5 D.极差是5
10、某校有11名同学参加某比赛,预赛成绩各不同,要取前6名参加决赛,小敏己经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这11名同学成绩的( )
A.最高分 B.中位数 C.极差 D.平均分
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、圆周率π≈3.141592653589793,数字5出现的频数是____.
2、为了庆祝中国共产党成立100周年,某校举行“歌唱祖国”班级合唱比赛,评委将从“舞台造型、合唱音准和进退场秩序”这三项进行打分,各项成绩均按百分制计算,然后再按舞台造型占40%,合唱音准占40%,进退场秩序占20%计算班级的综合成锁.七(1)班三项成绩依次是95分、90分、95分,则七(1)班的综合成绩为________.
3、有5个数据的平均数为24,另有15个数据的平均数是20,那么所有这20个数据的平均数是______.
4、甲、乙两同学5次数学考试的平均成绩都是132分,方差分别为S甲2=38,S乙2=10,则______ 同学的数学成绩更稳定.
5、一组数据的平均数是4,则这组数据的方差是_________.
三、解答题(5小题,每小题10分,共计50分)
1、为了让青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼.我校启动了“学生阳光体育短跑运动”,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补齐下面的表格:
次数 1 2 3 4 5
小明的成绩(秒) 13.3 13.4 13.3 ______ 13.3
小亮的成绩(秒) 13.2 ______ 13.1 13.5 13.3
(2)请写出小明的成绩的中位数和众数,小亮成绩的中位数;
(3)分别计算他们成绩的平均数和方差,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?
2、2021年4月13日,日本政府召开内阁会议正式决定,将福岛第一核电站超过100万公吨的核污水经过滤并稀释后排入大海,这一决定遭到包括福岛民众、日本渔民乃至国际社会的谴责和质疑.鉴于此次事件的恶劣影响,某校为了强化学生的环保意识,校团委在全校举办了“保护环境,人人有责”知识竞赛活动,初、高中根据初赛成绩,各选出5名选手组成初中代表队和高中代表队进行复赛,复赛成绩如图所示.
根据以上信息解答下列问题:
(1)高中代表队五名学生复赛成绩的中位数为 分;
(2)分别计算初中代表队、高中代表队学生复赛成绩的平均数;
(3)已知高中代表队学生复赛成绩的方差为20,请计算初中代表队学生复赛成绩的方差,并结合两队成绩的平均数和方差分析哪个队的复赛成绩较好.
3、某校为了增强学生的疫情防控意识,组织全校600名学生进行了疫情防控知识竞赛.从中随机抽取了名学生的竞赛成绩(满分100分,每名学生的成绩记为分),分成四组:组;组;组;组,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中信息,解答下列问题:
(1)求的值.
(2)补全频数分布直方图.
(3)若规定学生竞赛成绩为优秀,请估计全校竞赛成绩达到优秀的学生人数.
4、某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的满分均为100分,前6名选手的得分如下:
序号 1号 2号 3号 4号 5号
笔试成绩/分 85 92 84 90 84
面试成绩/分 90 88 86 90 80
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩.
(1)这6名选手笔试成绩的众数是 分.
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比.
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
5、随着经济的发展,我们身边的环境受到很大的影响,为了保护环境加强环保教育,某市实验中学组织500名学生参加义务收集废旧电池的活动,下面随机抽取50名学生对收集的废旧电池数量进行统计:
废旧电池数/节 3 4 5 6 8
人数/人 10 15 12 7 6
(1)这50名学生平均每人收集废旧电池多少节?
(2)这组废旧电池节数的中位数,众数分别是多少?
(3)根据统计发现,本次收集的各种废旧电池的数量比为:手机电池:7号电池:5号电池:1号电池=2:3:4:3,根据资料显示,各种电池1节能污染水的量之比为:手机电池:7号电池:5号电池:1号电池=6:1:2:3,且1节7号电池能使500吨的水受到污染,那么通过本次活动可减少受浸染的水多少吨?
-参考答案-
一、单选题
1、A
【分析】
可以设得总人数为x人,然后求得总钱数,再求平均数即可;在此题中购13元价格的饭菜的人最多,所以众数为13元.
【详解】
解:设本校共有师生x人,则买饭菜的费用是①12元:25%x×12=3x
②13元:55%x×13=7.15x,
③14元:20%x×14=2.8x
该校师生购买饭菜费用的平均数是(3x+7.15x+2.8x)÷x=12.95元.
购13元饭菜的人最多,所以众数为13元.
故选:A.
【点睛】
此题考查了众数与平均数的知识,属于简单题目.一组数据中出现次数最多的数据叫做众数.把所有数据相加后再除以数据的个数即得平均数.
2、D
【分析】
根据平均数、众数、中位数的定义以及方差公式计算即可得出答案.
【详解】
∵八年级5名参赛选手的成绩分别为:90,93,89,90,88,
从小到大排列为88,89,90,90,93,
∴平均数为,众数为90,中位数为90,
故选项A、B、C错误;
方差为,
故选项D正确.
故选:D.
【点睛】
本题考查平均数,众数和中位数,方差,掌握相关定义是解题的关键.
3、D
【分析】
先根据平均成绩选出,然后根据方差的意义求出
【详解】
解:根据平均数高,平均成绩好得出的性能好,
根据方差越小,数据波动越小可得出的性能好,
故选:D
【点睛】
本题主要考查了平均数和方差,熟练掌握平均数和方差的意义是解答本题的关键
4、A
【分析】
分别计算计算出甲乙选手的方差,根据方差越小数据越稳定解答即可.
【详解】
解:甲选手平均数为:,
乙选手平均数为:,
甲选手的方差为:,
乙选手的方差为:
∵可得出:,
则甲选手的成绩更稳定,
故选:A.
【点睛】
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
5、D
【分析】
根据数轴上的点与实数一一对应即可判断A;根据平均数相同的情形下,方差越小,成绩越稳定即可判断B;根据三角形的外角与内角的关系即可判断C;根据关于轴对称的点的坐标特征即可判断D
【详解】
A. 数轴上的每一个点都表示一个实数,故该选项不正确,不符合题意;
B. 甲、乙两人五次考试平均成绩相同,且,,则甲的成绩更稳定,故该选项不正确,不符合题意;
C. 三角形的一个外角不一定大于任意一个内角,故该选项不正确,不符合题意;
D. 在平面直角坐标系中,点与点关于x轴对称,故该选项正确,符合题意;
故选D
【点睛】
本题考查了实数与数轴,方差的意义,三角形的外角的性质,关于轴对称的点的坐标特征,掌握以上知识是解题的关键.
6、B
【分析】
根据题意和直方图中的数据可以求得质量在77.5kg及以上的生猪数,本题得以解决.
【详解】
解:由直方图可得,
质量在77.5kg及以上的生猪:90+30+20=140(头),
故选B.
【点睛】
本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
7、A
【分析】
根据方差的意义求解即可.
【详解】
解:∵S甲2=5,S乙2=20,S丙2=23,S丁2=32,
∴S甲2<S乙2<S丙2<S丁2,
∴这四名学生的数学成绩最稳定的是甲,
故选:A.
【点睛】
本题主要考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.
8、D
【分析】
根据中位数定义解答.将这组数据从小到大的顺序排列,第5、6个数的平均数为中位数.
【详解】
解:将这组数据从小到大的顺序排列处于中间位置的数即第5名和第6名的金牌数是36、27,
那么由中位数的定义可知,这组数据的中位数是.
故选D.
【点睛】
本题为统计题,考查中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
9、C
【分析】
计算这组数据的平均数、众数、中位数及极差即可作出判断.
【详解】
这组数据的平均数为:,众数为9,中位数为8.5,极差为10-7=3,故正确的是中位数为8.5.
故选:C
【点睛】
本题考查了反映一组数据平均数、众数、中位数、极差等知识,正确计算这些统计量是关键.
10、B
【分析】
由于共有11名同学参加某比赛,比赛取前6名参加决赛,根据中位数的意义分析即可.
【详解】
解:由于共有11个不同的成绩按从小到大排序后,中位数及中位数之后的共有6个数,
故只要知道自己的成绩和中位数就可以知道是否进入决赛了.
故选:B.
【点睛】
本题考查了中位数意义,解题的关键是正确掌握中位数的意义.
二、填空题
1、3
【分析】
从数5出现的次数即可得出答案.
【详解】
在中,5出现了3次,
∴数字5出现的频数是3.
故答案为:3.
【点睛】
本题考查频数的定义:一组数据中,某数据出现的次数,掌握频数的定义是解题的关键.
2、
【分析】
根据题意求这组数据的加权平均数即可.
【详解】
解:七(1)班的综合成绩为分
故答案为:
【点睛】
本题考查了求加权平均数,掌握加权平均数的计算是解题的关键,加权平均数计算公式为:,其中代表各数据的权.
3、21
【分析】
20个数据的总和为,故平均数为.
【详解】
解:
故答案为:.
【点睛】
本题考查了平均数.解题的关键是求出20个数据的总和.
4、乙
【分析】
根据平均数相同时,方差越小越稳定可以解答本题.
【详解】
解:∵甲、乙两同学5次数学考试的平均成绩都是132分,
方差分别为S甲2=38,S乙2=10,
∴S甲2S乙2,
∴乙同学的数学成绩更稳定,
故答案为:乙.
【点睛】
本题考查了方差,解题的关键是明确方差越小越稳定.
5、
【分析】
先根据平均数的定义求出x的值,再利用方差的定义列式计算即可.
【详解】
解:因为数据4,3,6,x的平均数是4,
可得:,
解得:x=3,
方差为:=,
故答案为:.
【点睛】
本题主要考查方差及算术平均数,解题的关键是掌握方差和平均数的定义.
三、解答题
1、(1)13.2,13.4;(2)小明:中位数13.3,众数13.3,小亮:中位数13.3;(3)小明的成绩比较稳定,因此对小亮的建议要加强稳定性训练,而小明应该加强爆发力训练,提高训练成绩.
【分析】
(1)从统计图中可得到每次百米训练的成绩,从而填入表格即可;
(2)根据中位数、众数的意义求出结果即可;
(3)计算两人的平均数、方差,再比较得出结论.
【详解】
解:(1)从统计图可知,小明第次的成绩为,小亮第次的成绩为,
故答案为:,;补全的表格如下:
次数 1 2 3 4 5
小明 13.3 13.4 13.3 13.2 13. 3
小亮 13.2 13.4 13.1 13.5 13.3
(2)小明次成绩的中位数是,众数为;
小亮次成绩的中位数是;
(3)小明
小亮
∴小明
小亮
∵小明小亮
∴小明小亮
∴小明的成绩比较稳定,因此对小亮的建议要加强稳定性训练,而小明应该加强爆发力训练,提高训练成绩.
【点睛】
本题考查折线统计图、加权平均数、中位数、众数以及方差的意义和计算方法,明确各个统计量的意义是正确解答的前提.
2、(1)95;(2)高中代表队的平均数为95分,初中代表队的平均数为90分;(3)初中代表队学生复赛成绩的方差为40,高中代表队成绩较好.
【分析】
(1)根据中位数的定义求解即可;
(2)根据平均数的定义求解即可;
(3)根据方差的定义求出初中代表队学生复赛成绩的方差,然后根据平均数和方差越小越稳定判断即可.
【详解】
解:(1)五个人的成绩从小到大排列为:90,90,95,100,100,
一共有5个数,第3个数为中位数,
∴中位数是95;
(2)高中代表队的平均数=(分),
初中代表队的平均数=(分);
(3)初中代表队学生复赛成绩的方差=,
∵,
∴高中代表队成绩较好.
【点睛】
此题考查了平均数,中位数和方差及其意义,解题的关键是熟练掌握平均数,中位数和方差的求解方法.
3、(1)50;(2)见解析;(3)180人
【分析】
(1)根据组的频数和所占的百分比,可以求得的值;
(2)根据(1)中的值和频数分布直方图中的数据,可以计算出组的频数,从而可以将频数分布直方图补充完整;
(3)根据直方图中的数据,可以计算出全校成绩达到优秀的人数.
【详解】
解:(1);
(2)组学生有:(人),
补全的频数分布直方图如图所示;
(3)(人),
答:估算全校成绩达到优秀的有180人.
【点睛】
本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确统计图的特点和中位数的含义,利用数形结合的思想解答.
4、(1)84;(2)笔试成绩和面试成绩各占的百分比是40%,60%;(3)2号:89.6分,3号:85.2分,4号:90分,5号:81.6分,6号:83分,综合成绩排序前两名人选是4号和2号
【分析】
(1)根据中位数和众数的定义即把这组数据从小到大排列,再找出最中间两个数的平均数就是中位数,再找出出现的次数最多的数即是众数;
(2)先设笔试成绩和面试成绩各占的百分百是x,y,根据题意列出方程组,求出x,y的值即可;
(3)根据笔试成绩和面试成绩各占的百分比,分别求出其余五名选手的综合成绩,即可得出答案.
【详解】
解:(1)把这组数据从小到大排列为,80,84,84,85,90,92,
84出现了2次,出现的次数最多,则这6名选手笔试成绩的众数是84分;
故答案为:84;
(2)设笔试成绩和面试成绩各占的百分比是x,y,根据题意得:
,
解得,
∴笔试成绩和面试成绩各占的百分比是40%,60%.
(3)2号选手的综合成绩是92×0.4+88×0.6=89.6(分),
3号选手的综合成绩是84×0.4+86×0.6=85.2(分),
4号选手的综合成绩是90×0.4+90×0.6=90(分),
5号选手的综合成绩是84×0.4+80×0.6=81.6(分),
6号选手的综合成绩是80×0.4+85×0.6=83(分).
∴综合成绩排序前两名人选是4号和2号.
【点睛】
本题考查了众数、二元一次方程组的实际应用,加权平均数等知识点,依据题意,正确建立方程求出题(2)中的笔试成绩和面试成绩各占的百分比是解题的关键.
5、(1)4.8节;(2)众数为4个,中位数为4.5节;(3)本次活动可减少受浸染的水3200000吨.
【分析】
(1)求出50名学生收集废旧电池的总数,再求平均数即可;
(2)从统计表格即可求得众数为5,然后按从大到小给所有数据排序,求出中位数即可;
(3)先求出这些电池可污染的水的数量即可解决问题.
【详解】
解:(1)50名学生平均每人收集废旧电池的节数=(10×3+15×4+12×5+7×6+6×8)÷50=4.8(节);
(2)从统计表格得,众数为4节;
由于收集3节和4节电池的人数有25个人,收集5节的人有12人,所以中位数=(4+5)÷2=4.5(节);
(3)样本中电池总数4.8×50=240,
由于本次收集的各种电池的数量比为:手机电池:7号电池:5号电池:1号电池=2:3:4:3,
故可得出手机电池、7号电池、5号电池、1号电池与总数的比值分别为:
,,,,即,,,,
由于各种电池1节能污染水的量的比为:手机电池:7号电池:5号电池:1号电池=6:1:2:3,且1节7号电池能使500吨的水受到污染,故可得手机电池、5号电池、1号电池一节分别能污染水的吨数为500×6,500×2,500×3,
故在50名学生收集的废电池可少受污染水的吨数为
=320000(吨)
320000÷50×500=3200000吨,
答:本次活动可减少受浸染的水3200000吨.
【点睛】
本题考查了从统计图中获取信息的能力;对平均数、中位数和众数等概念的掌握程度.同时通过此题倡导学生参加义务收集废旧电池活动中来.
