第九章 统计 章末小结复习课 课件(共42张PPT)
文档属性
| 名称 | 第九章 统计 章末小结复习课 课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-09 18:08:24 | ||
图片预览







文档简介
(共42张PPT)
第九章 统计 章末复习小结课
人教A版(2019)
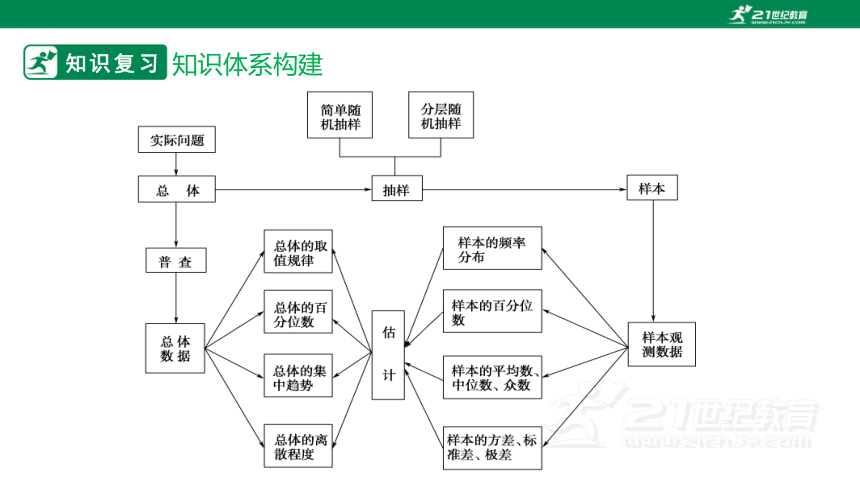
知识复习
知识体系构建
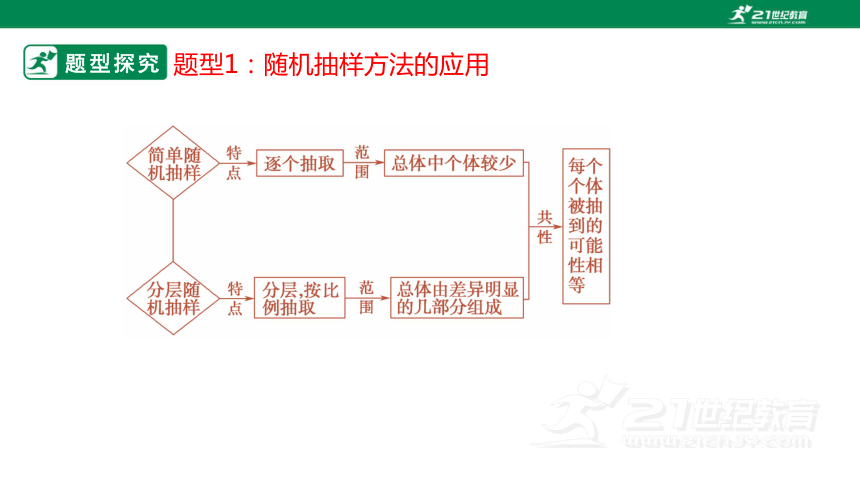
题型探究
题型1:随机抽样方法的应用
随机抽样有简单随机抽样和分层随机抽样两种.其共同点是在抽样过程中每个个体被抽到的机会相等,当总体中的个体数较少时,常采用简单随机抽样;当已知总体由差异明显的几部分组成时,常采用分层随机抽样.其中简单随机抽样是最简单、最基本的抽样方法.分层随机抽样时一般要用到简单随机抽样.
应用各种抽样方法抽样时要注意以下问题:
①利用抽签法时要注意把号签放在不透明的容器中且搅拌均匀;
②利用随机数法时注意编号位数要一致;
③在分层随机抽样中,若在某一层按比例应该抽取的个体数不是整数,应在该层剔除部分个体,使抽取个体数为整数.
题型探究
【例1】⑴从一个篮球训练营中抽取10名学员进行投篮比赛,每人投10次,统计出该
10名学员投篮投中的次数,4个投中5次,3个投中6次,2个投中7次,1个投中8次.试估计该训练营投篮投中的比例为________.
⑵某班对八校联考成绩进行分析,利用随机数表法抽取样本时,先将70个同学
按01,02,03,…,70进行编号,然后从随机数表第9行第9列的数开始向右读,
则选出的第7个个体是( )
(注:如表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54.
A.07 B.44 C.15 D.51
解:
⑴10名学员投中的平均数为=6.
⑵找到第9行第9列数开始向右读,符合条件的是29,64,56,07,52,42,44,
∴投中的比例为=0.6.
∴选出的第7个个体是44.故选B.
B
题型1:随机抽样方法的应用
0.6
题型探究
【例2】某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,干事20人,上级机关为了了解机关人员对政府机构的改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,如何抽取?
解:
用分层随机抽样抽取.
∵20∶100=1∶5,
∴ =2, =14, =4,
即从副处级以上干部中抽取2人,一般干部中抽取14人,干事中抽取4人.
因为副处级以上干部与干事人数都较少,他们分别按1~10编号和1~20编号,然后采用抽签法分别抽取2人和4人;
对一般干部采用00,01,…,69编号,然后用随机数法抽取14人.
题型1:随机抽样方法的应用
题型探究
题型1:随机抽样方法的应用
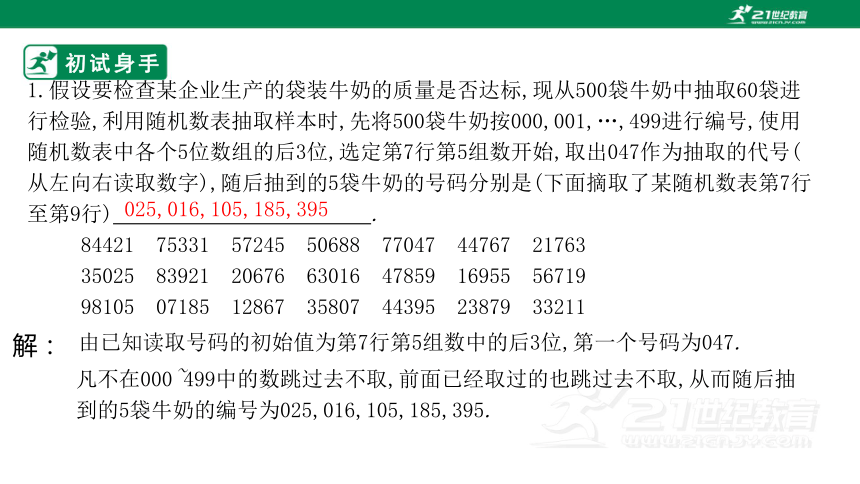
初试身手
1.假设要检查某企业生产的袋装牛奶的质量是否达标,现从500袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将500袋牛奶按000,001,…,499进行编号,使用随机数表中各个5位数组的后3位,选定第7行第5组数开始,取出047作为抽取的代号(从左向右读取数字),随后抽到的5袋牛奶的号码分别是(下面摘取了某随机数表第7行至第9行) .
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
解:
由已知读取号码的初始值为第7行第5组数中的后3位,第一个号码为047.
凡不在000~499中的数跳过去不取,前面已经取过的也跳过去不取,从而随后抽到的5袋牛奶的编号为025,016,105,185,395.
025,016,105,185,395
初试身手
2.校高中生共有2 700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为27的样本,那么高一、高二、高三各年级抽取的人数分别为( )
A.6,12,9 B.9,9,9 C.3,9,15 D.9,12,6.
解:
由题意得,用分层抽样在各层中的抽样比为27:2700=,
∴在高一年级抽取的人数是=9人.
高二年级抽取的人数是=12人,
高三年级抽取的人数是=6人.
则高一、高二、高三各年级抽取的人数分别为9,12,6. 故选D.
D
初试身手
3.经问卷调查,某班学生对摄影分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的学生比持“不喜欢”态度的学生多12人,用分层抽样的方法从全班中选出部分学生进行摄影知识座谈,如果选出的是5位“喜欢”摄影的学生、1位“不喜欢”摄影的学生和3位持“一般”态度的学生,那么全班学生中“喜欢”摄影的人数比全班学生人数的一半还多________人.
解:
设班里学生持“喜欢”态度的有y人,持“一般”态度的有x人,则持“不喜欢”态度的有(12-x)人,
∵采用分层抽样的方法,∴y:(12-x):x=5:1:3
解得 x=18,y=30.
则全班共有30+6+18=54(人).
又30-=3.
3
即全班学生中“喜欢”摄影的人数比全班学生人数的一半还多3人.
题型探究
题型2:频率分布直方图及应用
总体分布中相应的统计图表主要包括:频率分布表、频率分布直方图、频率分布折线图等.通过这些统计图表给出的相应统计信息可以估计总体.
绘制频率分布直方图的步骤
一组数据中最大值与最小值的差
组数若则组数若则组数为不小于的最小整数
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
1.求极差
2.决定组距和组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
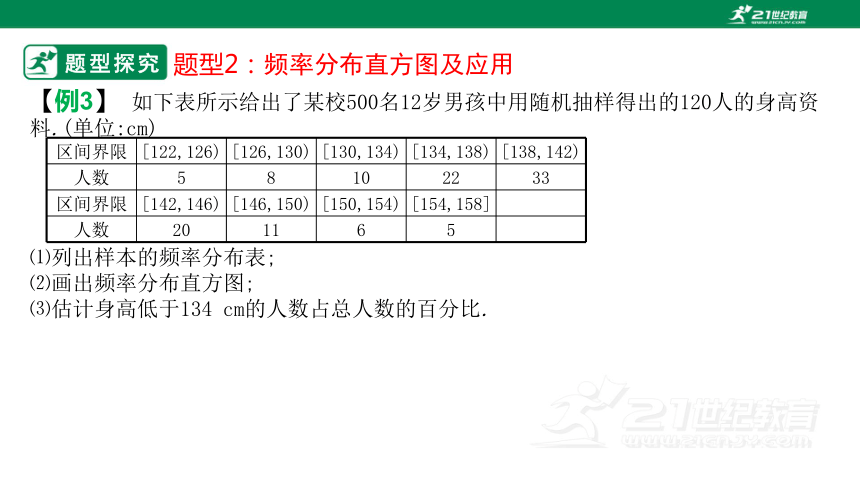
题型探究
【例3】 如下表所示给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料.(单位:cm)
⑴列出样本的频率分布表;
⑵画出频率分布直方图;
⑶估计身高低于134 cm的人数占总人数的百分比.
题型2:频率分布直方图及应用
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
题型探究
解:
题型2:频率分布直方图及应用
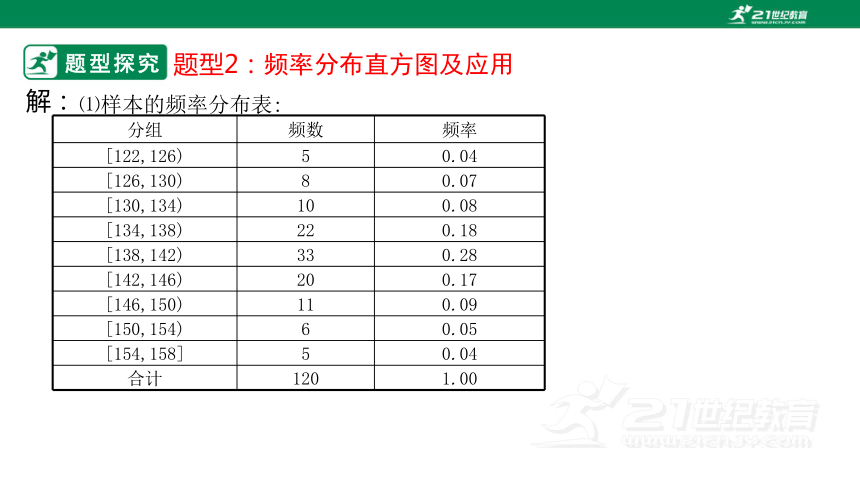
⑴样本的频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
题型探究
解:
题型2:频率分布直方图及应用
⑵画出频率分布直方图,如下图所示:
⑶因为样本中身高低于134 cm的人数的频率为0.04+0.07+0.08=0.19
所以估计身高低于134 cm的人数约占总人数的19%.
题型探究
题型2:频率分布直方图及应用
用样本估计总体分布的方法
⑴用样本频率分布估计总体频率分布时,通常要对给定的一组数据进行列表、作图处理,作频率分布表与频率分布直方图时要注意其方法步骤.
⑵借助图表,可以把抽样获得的庞杂数据变得直观,凸显其中的规律,便于信息的提取和交流.
初试身手
4.某花木公司为了调查某种树苗的生长情况,抽取了一个容量为100的样本,测得树苗的高度(cm)数据的分组及相应频数如下:
[107,109),3株;[109,111), 9株;[111,113),13株;
[113,115),16株;[115,117),26株;[117,119),20株;
[119,121),7株;[121,123),4株;[123,125],2株.
⑴列出频率分布表;
⑵画出频率分布直方图;
⑶据上述图表,估计数据在[109,121)范围内的可能性是百分之几?
题型2:频率分布直方图及应用
初试身手
题型2:频率分布直方图及应用
解:
[107,109),3株;[109,111), 9株;[111,113),13株;[113,115),16株;[115,117),26株;[117,119),20株;[119,121),7株;[121,123),4株;[123,125],2株.
⑴列出频率分布表
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
初试身手
题型2:频率分布直方图及应用
解:
⑵画出频率分布直方图
⑶由上述图表可知数据落在[109,121)范围内的频率为:0.94-0.03=0.91,
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
即数据落在[109,121)范围内的可能性是91%.
初试身手
题型2:频率分布直方图及应用
5.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,
将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,
下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
初试身手
题型2:频率分布直方图及应用
解:
因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.
用样本频率直方图中的频率即可作为总体的相应比率的估计值.
该地农户家庭年收入低于4.5万元的农户比率估计值为0.02+0.04=0.06=6%,故A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计值为
0.04+0.02×3=0.10=10%,故B正确;
该地农户家庭年收入介于4.5万元至8.5万元之间
的比例估计值为0.10+0.14+0.20×2=0.64=64%>50%,
故D正确;
该地农户家庭年收入的平均值的估计值为
3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68>6.5(万元),则C错误.故选C.
新知探究
题型3:总体百分位数的估计
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
计算一组n个数据的第p百分位数的步骤.
第1步:按从小到大排列原始数据.
第2步:计算i=n×p%.
若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均数.
第3步:若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
常用的百分位数.
①四分位数: , , .
②其它常用的百分位数:1%,5%,10%,80%,90%,95%,99%.
25%
50%
75%
题型探究
【例4】我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图所示的频率分布直方图.
⑴假设同组中的每个数据都用该组区间的中点
值代替,求全市家庭月均用水量平均数的估计
值(精确到0.01);
题型3:总体百分位数的估计
解:
⑴因为0.06×2×1+0.11×2×3+0.18×2×5+0.09×2×7+0.06×2×9=4.92
所以全市家庭月均用水量的平均数估计值为4.92 t.
题型探究
【例4】我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图所示的频率分布直方图.
⑵求全市家庭月均用水量的25%分位数的估计
值(精确到0.01).
题型3:总体百分位数的估计
解:
⑵由于频率分布直方图中,用水量低于2t的频率为0.06×2=0.12,
用水量低于4t的频率为0.06×2+0.11×2=0.34,
所以全市家庭月均用水量的25%分位数的估计值为
2+3.18(t).
题型探究
题型3:总体百分位数的估计
百分位数是用于衡量数据的位置的量度,但它所衡量的,不一定是中心位置.百分位数提供了有关各数据项如何在最小值与最大值之间分布的信息.对于无大量重复的数据,第p百分位数将它分为两个部分.至少有p%的数据项的值小于或等于第p百分位数;而至少有(100-p)%的数据项的值大于或等于第p百分位数.对第p百分位数,严格的定义如下:第p百分位数是这样一个值,它使得至少有p%的数据项小于或等于这个值,且至少有(100-p)%的数据项大于或等于这个值.
初试身手
6.下表为12名毕业生的起始月薪
根据表中所给的数据计算第85百分位数.
毕业生 起始月薪 毕业生 起始月薪
1 2 850 7 2 890
2 2 950 8 3 130
3 3 050 9 2 940
4 2 880 10 3 325
5 2 755 11 2 920
6 2 710 12 2 880
题型3:总体百分位数的估计
初试身手
题型3:总体百分位数的估计
将12个数据按从小到大排序:2710,2755,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325.
解:
计算i=12×85%=10.2,
所以所给数据的第85百分位数是第11个数据3130.
题型探究
题型4:总体集中趋势的估计
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少一部分,对极端值也不敏感.
一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
平均数、众数、中位数是反映样本数据集中趋势的.
平均数的大小与一组数据里的每个数均有关系,其中任何数据的变动都会相应引起平均数的变动;众数着眼于对各数据出现频率的考察,其大小只与这组数据的部分数据有关;中位数仅与数据的排列有关,部分数据的变动对中位数可能没有影响.
题型探究
【例5】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
题型4:总体集中趋势的估计
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
⑴求乙离子残留百分比直方图中a,b的值;
⑵分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
题型探究
解:
⑴由已知得0.70=(a+0.20+0.15)×1,
乙离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
∴a=0.35,b=1-0.05-0.15-0.70=0.10.
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
⑵甲离子残留百分比的平均值的估计值为
题型4:总体集中趋势的估计
初试身手
7.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的统计表如表所示:
有以下四种说法:
①甲成绩的平均数小于乙成绩的平均数;
②甲成绩的中位数等于乙成绩的中位数;
③甲成绩的极差小于乙成绩的极差;
④甲成绩的众数小于乙成绩的众数.
其中正确命题的个数是( )
A.1 B.2 C.3 D.0
题型4:总体集中趋势的估计
甲 乙 环数 4 5 6 7 8 环数 5 6 9
频数 1 1 1 1 1 频数 3 1 1
初试身手
题型4:总体集中趋势的估计
解:
由表中数据,计算=×(4+5+6+7+8)=6,
×(5×3+6+9)=6,
∴=,①错误;
甲成绩的中位数是6,乙成绩的中位数是5,所以甲的中位数大于乙的中位数,②错误;
由甲成绩的极差为8-4=4,乙成绩的极差为9-5=4,所以甲成绩的极差等于乙成绩的极差,③错误;
由于乙成绩的众数为5,而4,5,6,7,8都是甲成绩的众数,所以乙成绩的众数与甲成绩的众数无法比较大小,④错误.
则正确命题的个数为0,故选D.
题型探究
题型5:总体离散程度的估计
反映样本数据离散程度的包括样本方差及标准差.
标准差刻画了数据的数据的离散程度或波动幅度.标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小;显然,在刻画数据的分散程度上,方差和标准差是一样的,但在解决实际问题中,一般多采用标准差.
在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
第一层样本记为x1,x2,…,xn,其平均数记为,方差记为;第二层样本记为y1,y2,…,ym,其平均数记为,方差记为;总体数据样本的平均数记为,方差记为,则
题型探究
【例6】某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10)
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为,样本方差为s2.
⑴求,s2;
解:
题型5:总体离散程度的估计
试验序号i 1 2 3 4 5 6 7 8 9 10
伸缩率xi 545 533 551 522 575 544 541 568 596 548
伸缩率yi 536 527 543 530 560 533 522 550 576 536
⑴∵z1=9,z2=6,z3=8,z4=-8,z5=15,z6=11,z7=19,z8=18,z9=20,z10=12,
∴=11.
=61.
题型探究
【例6】某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10)
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为,样本方差为s2.
⑵判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高).
解:
题型5:总体离散程度的估计
试验序号i 1 2 3 4 5 6 7 8 9 10
伸缩率xi 545 533 551 522 575 544 541 568 596 548
伸缩率yi 536 527 543 530 560 533 522 550 576 536
⑵由⑴得=11,=61,而.∴.
则可以认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.
题型探究
【例7】某校为了解高三年级学生的身高情况,根据男女学生所占的比例,利用分层随机抽样分别抽取50名男生和30名女生,测量他们的身高,所得数据如下:
试估计该校高三年级学生身高的平均数和方差.
解:
=169.5(cm),
由题意可得,样本平均数为
则可估计该校高三年级学生身高的平均数为169.5cm,方差为194.375.
方差
=194.375.
性别 人数 平均数(cm) 方差
男生 50 174 191
女生 30 162 110
题型5:总体离散程度的估计
初试身手
8.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
⑴求甲成绩的80%分位数;
解:
把甲的成绩按照从小到大的顺序排列可得:
78 79 81 82 84 88 93 95
因为一共有8个数据,所以8×80%=6.4,不是整数,
所以甲成绩的80%分位数是第7个数据93.
题型5:总体离散程度的估计
初试身手
8.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
⑵现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由?
解:
甲= (78+79+81+82+84+88+93+95)=85
乙= (75+80+80+83+85+90+92+95)=85
∵ 甲= 乙, < ,
= [(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5.
= [(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
∴甲的成绩较稳定,派甲参赛比较合适.
题型5:总体离散程度的估计
初试身手
9.某厂研究了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为s12和s22.
⑴求,,s12,s22;
解:
=10.3,
⑴=10.0,
=0.036.
题型5:总体离散程度的估计
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
=0.04.
初试身手
9.某厂研究了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为s12和s22.
⑵判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
解:
⑵由⑴得,10.3-10.0=0.3=2,.
∴新设备生产产品的该项指标的均值较旧设备有显著提高.
题型5:总体离散程度的估计
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
∴.
作业布置
作业: p224-226 复习参考题9 第7,8,9,10,11题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第九章 统计 章末复习小结课
人教A版(2019)
知识复习
知识体系构建
题型探究
题型1:随机抽样方法的应用
随机抽样有简单随机抽样和分层随机抽样两种.其共同点是在抽样过程中每个个体被抽到的机会相等,当总体中的个体数较少时,常采用简单随机抽样;当已知总体由差异明显的几部分组成时,常采用分层随机抽样.其中简单随机抽样是最简单、最基本的抽样方法.分层随机抽样时一般要用到简单随机抽样.
应用各种抽样方法抽样时要注意以下问题:
①利用抽签法时要注意把号签放在不透明的容器中且搅拌均匀;
②利用随机数法时注意编号位数要一致;
③在分层随机抽样中,若在某一层按比例应该抽取的个体数不是整数,应在该层剔除部分个体,使抽取个体数为整数.
题型探究
【例1】⑴从一个篮球训练营中抽取10名学员进行投篮比赛,每人投10次,统计出该
10名学员投篮投中的次数,4个投中5次,3个投中6次,2个投中7次,1个投中8次.试估计该训练营投篮投中的比例为________.
⑵某班对八校联考成绩进行分析,利用随机数表法抽取样本时,先将70个同学
按01,02,03,…,70进行编号,然后从随机数表第9行第9列的数开始向右读,
则选出的第7个个体是( )
(注:如表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54.
A.07 B.44 C.15 D.51
解:
⑴10名学员投中的平均数为=6.
⑵找到第9行第9列数开始向右读,符合条件的是29,64,56,07,52,42,44,
∴投中的比例为=0.6.
∴选出的第7个个体是44.故选B.
B
题型1:随机抽样方法的应用
0.6
题型探究
【例2】某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,干事20人,上级机关为了了解机关人员对政府机构的改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,如何抽取?
解:
用分层随机抽样抽取.
∵20∶100=1∶5,
∴ =2, =14, =4,
即从副处级以上干部中抽取2人,一般干部中抽取14人,干事中抽取4人.
因为副处级以上干部与干事人数都较少,他们分别按1~10编号和1~20编号,然后采用抽签法分别抽取2人和4人;
对一般干部采用00,01,…,69编号,然后用随机数法抽取14人.
题型1:随机抽样方法的应用
题型探究
题型1:随机抽样方法的应用
初试身手
1.假设要检查某企业生产的袋装牛奶的质量是否达标,现从500袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将500袋牛奶按000,001,…,499进行编号,使用随机数表中各个5位数组的后3位,选定第7行第5组数开始,取出047作为抽取的代号(从左向右读取数字),随后抽到的5袋牛奶的号码分别是(下面摘取了某随机数表第7行至第9行) .
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
解:
由已知读取号码的初始值为第7行第5组数中的后3位,第一个号码为047.
凡不在000~499中的数跳过去不取,前面已经取过的也跳过去不取,从而随后抽到的5袋牛奶的编号为025,016,105,185,395.
025,016,105,185,395
初试身手
2.校高中生共有2 700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为27的样本,那么高一、高二、高三各年级抽取的人数分别为( )
A.6,12,9 B.9,9,9 C.3,9,15 D.9,12,6.
解:
由题意得,用分层抽样在各层中的抽样比为27:2700=,
∴在高一年级抽取的人数是=9人.
高二年级抽取的人数是=12人,
高三年级抽取的人数是=6人.
则高一、高二、高三各年级抽取的人数分别为9,12,6. 故选D.
D
初试身手
3.经问卷调查,某班学生对摄影分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的学生比持“不喜欢”态度的学生多12人,用分层抽样的方法从全班中选出部分学生进行摄影知识座谈,如果选出的是5位“喜欢”摄影的学生、1位“不喜欢”摄影的学生和3位持“一般”态度的学生,那么全班学生中“喜欢”摄影的人数比全班学生人数的一半还多________人.
解:
设班里学生持“喜欢”态度的有y人,持“一般”态度的有x人,则持“不喜欢”态度的有(12-x)人,
∵采用分层抽样的方法,∴y:(12-x):x=5:1:3
解得 x=18,y=30.
则全班共有30+6+18=54(人).
又30-=3.
3
即全班学生中“喜欢”摄影的人数比全班学生人数的一半还多3人.
题型探究
题型2:频率分布直方图及应用
总体分布中相应的统计图表主要包括:频率分布表、频率分布直方图、频率分布折线图等.通过这些统计图表给出的相应统计信息可以估计总体.
绘制频率分布直方图的步骤
一组数据中最大值与最小值的差
组数若则组数若则组数为不小于的最小整数
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
1.求极差
2.决定组距和组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
题型探究
【例3】 如下表所示给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料.(单位:cm)
⑴列出样本的频率分布表;
⑵画出频率分布直方图;
⑶估计身高低于134 cm的人数占总人数的百分比.
题型2:频率分布直方图及应用
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
题型探究
解:
题型2:频率分布直方图及应用
⑴样本的频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
题型探究
解:
题型2:频率分布直方图及应用
⑵画出频率分布直方图,如下图所示:
⑶因为样本中身高低于134 cm的人数的频率为0.04+0.07+0.08=0.19
所以估计身高低于134 cm的人数约占总人数的19%.
题型探究
题型2:频率分布直方图及应用
用样本估计总体分布的方法
⑴用样本频率分布估计总体频率分布时,通常要对给定的一组数据进行列表、作图处理,作频率分布表与频率分布直方图时要注意其方法步骤.
⑵借助图表,可以把抽样获得的庞杂数据变得直观,凸显其中的规律,便于信息的提取和交流.
初试身手
4.某花木公司为了调查某种树苗的生长情况,抽取了一个容量为100的样本,测得树苗的高度(cm)数据的分组及相应频数如下:
[107,109),3株;[109,111), 9株;[111,113),13株;
[113,115),16株;[115,117),26株;[117,119),20株;
[119,121),7株;[121,123),4株;[123,125],2株.
⑴列出频率分布表;
⑵画出频率分布直方图;
⑶据上述图表,估计数据在[109,121)范围内的可能性是百分之几?
题型2:频率分布直方图及应用
初试身手
题型2:频率分布直方图及应用
解:
[107,109),3株;[109,111), 9株;[111,113),13株;[113,115),16株;[115,117),26株;[117,119),20株;[119,121),7株;[121,123),4株;[123,125],2株.
⑴列出频率分布表
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
初试身手
题型2:频率分布直方图及应用
解:
⑵画出频率分布直方图
⑶由上述图表可知数据落在[109,121)范围内的频率为:0.94-0.03=0.91,
分组 频数 频率 累积频率
[107,109) 3 0.03 0.03
[109,111) 9 0.09 0.12
[111,113) 13 0.13 0.25
[113,115) 16 0.16 0.41
[115,117) 26 0.26 0.67
[117,119) 20 0.20 0.87
[119,121) 7 0.07 0.94
[121,123) 4 0.04 0.98
[123,125] 2 0.02 1.00
合计 100 1.00
即数据落在[109,121)范围内的可能性是91%.
初试身手
题型2:频率分布直方图及应用
5.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,
将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,
下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
初试身手
题型2:频率分布直方图及应用
解:
因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.
用样本频率直方图中的频率即可作为总体的相应比率的估计值.
该地农户家庭年收入低于4.5万元的农户比率估计值为0.02+0.04=0.06=6%,故A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计值为
0.04+0.02×3=0.10=10%,故B正确;
该地农户家庭年收入介于4.5万元至8.5万元之间
的比例估计值为0.10+0.14+0.20×2=0.64=64%>50%,
故D正确;
该地农户家庭年收入的平均值的估计值为
3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68>6.5(万元),则C错误.故选C.
新知探究
题型3:总体百分位数的估计
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
计算一组n个数据的第p百分位数的步骤.
第1步:按从小到大排列原始数据.
第2步:计算i=n×p%.
若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均数.
第3步:若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
常用的百分位数.
①四分位数: , , .
②其它常用的百分位数:1%,5%,10%,80%,90%,95%,99%.
25%
50%
75%
题型探究
【例4】我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图所示的频率分布直方图.
⑴假设同组中的每个数据都用该组区间的中点
值代替,求全市家庭月均用水量平均数的估计
值(精确到0.01);
题型3:总体百分位数的估计
解:
⑴因为0.06×2×1+0.11×2×3+0.18×2×5+0.09×2×7+0.06×2×9=4.92
所以全市家庭月均用水量的平均数估计值为4.92 t.
题型探究
【例4】我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图所示的频率分布直方图.
⑵求全市家庭月均用水量的25%分位数的估计
值(精确到0.01).
题型3:总体百分位数的估计
解:
⑵由于频率分布直方图中,用水量低于2t的频率为0.06×2=0.12,
用水量低于4t的频率为0.06×2+0.11×2=0.34,
所以全市家庭月均用水量的25%分位数的估计值为
2+3.18(t).
题型探究
题型3:总体百分位数的估计
百分位数是用于衡量数据的位置的量度,但它所衡量的,不一定是中心位置.百分位数提供了有关各数据项如何在最小值与最大值之间分布的信息.对于无大量重复的数据,第p百分位数将它分为两个部分.至少有p%的数据项的值小于或等于第p百分位数;而至少有(100-p)%的数据项的值大于或等于第p百分位数.对第p百分位数,严格的定义如下:第p百分位数是这样一个值,它使得至少有p%的数据项小于或等于这个值,且至少有(100-p)%的数据项大于或等于这个值.
初试身手
6.下表为12名毕业生的起始月薪
根据表中所给的数据计算第85百分位数.
毕业生 起始月薪 毕业生 起始月薪
1 2 850 7 2 890
2 2 950 8 3 130
3 3 050 9 2 940
4 2 880 10 3 325
5 2 755 11 2 920
6 2 710 12 2 880
题型3:总体百分位数的估计
初试身手
题型3:总体百分位数的估计
将12个数据按从小到大排序:2710,2755,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325.
解:
计算i=12×85%=10.2,
所以所给数据的第85百分位数是第11个数据3130.
题型探究
题型4:总体集中趋势的估计
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少一部分,对极端值也不敏感.
一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
平均数、众数、中位数是反映样本数据集中趋势的.
平均数的大小与一组数据里的每个数均有关系,其中任何数据的变动都会相应引起平均数的变动;众数着眼于对各数据出现频率的考察,其大小只与这组数据的部分数据有关;中位数仅与数据的排列有关,部分数据的变动对中位数可能没有影响.
题型探究
【例5】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
题型4:总体集中趋势的估计
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
⑴求乙离子残留百分比直方图中a,b的值;
⑵分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
题型探究
解:
⑴由已知得0.70=(a+0.20+0.15)×1,
乙离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
∴a=0.35,b=1-0.05-0.15-0.70=0.10.
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
⑵甲离子残留百分比的平均值的估计值为
题型4:总体集中趋势的估计
初试身手
7.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的统计表如表所示:
有以下四种说法:
①甲成绩的平均数小于乙成绩的平均数;
②甲成绩的中位数等于乙成绩的中位数;
③甲成绩的极差小于乙成绩的极差;
④甲成绩的众数小于乙成绩的众数.
其中正确命题的个数是( )
A.1 B.2 C.3 D.0
题型4:总体集中趋势的估计
甲 乙 环数 4 5 6 7 8 环数 5 6 9
频数 1 1 1 1 1 频数 3 1 1
初试身手
题型4:总体集中趋势的估计
解:
由表中数据,计算=×(4+5+6+7+8)=6,
×(5×3+6+9)=6,
∴=,①错误;
甲成绩的中位数是6,乙成绩的中位数是5,所以甲的中位数大于乙的中位数,②错误;
由甲成绩的极差为8-4=4,乙成绩的极差为9-5=4,所以甲成绩的极差等于乙成绩的极差,③错误;
由于乙成绩的众数为5,而4,5,6,7,8都是甲成绩的众数,所以乙成绩的众数与甲成绩的众数无法比较大小,④错误.
则正确命题的个数为0,故选D.
题型探究
题型5:总体离散程度的估计
反映样本数据离散程度的包括样本方差及标准差.
标准差刻画了数据的数据的离散程度或波动幅度.标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小;显然,在刻画数据的分散程度上,方差和标准差是一样的,但在解决实际问题中,一般多采用标准差.
在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
第一层样本记为x1,x2,…,xn,其平均数记为,方差记为;第二层样本记为y1,y2,…,ym,其平均数记为,方差记为;总体数据样本的平均数记为,方差记为,则
题型探究
【例6】某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10)
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为,样本方差为s2.
⑴求,s2;
解:
题型5:总体离散程度的估计
试验序号i 1 2 3 4 5 6 7 8 9 10
伸缩率xi 545 533 551 522 575 544 541 568 596 548
伸缩率yi 536 527 543 530 560 533 522 550 576 536
⑴∵z1=9,z2=6,z3=8,z4=-8,z5=15,z6=11,z7=19,z8=18,z9=20,z10=12,
∴=11.
=61.
题型探究
【例6】某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10)
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为,样本方差为s2.
⑵判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高).
解:
题型5:总体离散程度的估计
试验序号i 1 2 3 4 5 6 7 8 9 10
伸缩率xi 545 533 551 522 575 544 541 568 596 548
伸缩率yi 536 527 543 530 560 533 522 550 576 536
⑵由⑴得=11,=61,而.∴.
则可以认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.
题型探究
【例7】某校为了解高三年级学生的身高情况,根据男女学生所占的比例,利用分层随机抽样分别抽取50名男生和30名女生,测量他们的身高,所得数据如下:
试估计该校高三年级学生身高的平均数和方差.
解:
=169.5(cm),
由题意可得,样本平均数为
则可估计该校高三年级学生身高的平均数为169.5cm,方差为194.375.
方差
=194.375.
性别 人数 平均数(cm) 方差
男生 50 174 191
女生 30 162 110
题型5:总体离散程度的估计
初试身手
8.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
⑴求甲成绩的80%分位数;
解:
把甲的成绩按照从小到大的顺序排列可得:
78 79 81 82 84 88 93 95
因为一共有8个数据,所以8×80%=6.4,不是整数,
所以甲成绩的80%分位数是第7个数据93.
题型5:总体离散程度的估计
初试身手
8.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
⑵现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由?
解:
甲= (78+79+81+82+84+88+93+95)=85
乙= (75+80+80+83+85+90+92+95)=85
∵ 甲= 乙, < ,
= [(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5.
= [(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
∴甲的成绩较稳定,派甲参赛比较合适.
题型5:总体离散程度的估计
初试身手
9.某厂研究了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为s12和s22.
⑴求,,s12,s22;
解:
=10.3,
⑴=10.0,
=0.036.
题型5:总体离散程度的估计
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
=0.04.
初试身手
9.某厂研究了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为s12和s22.
⑵判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
解:
⑵由⑴得,10.3-10.0=0.3=2,.
∴新设备生产产品的该项指标的均值较旧设备有显著提高.
题型5:总体离散程度的估计
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
∴.
作业布置
作业: p224-226 复习参考题9 第7,8,9,10,11题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
