北师大版数学九年级下册第一章直角三角形边角关系单元练习题(含答案)
文档属性
| 名称 | 北师大版数学九年级下册第一章直角三角形边角关系单元练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 412.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 12:15:23 | ||
图片预览



文档简介
北师大版九年级下册第一章直角三角形边角关系单元练习题
一.选择题(共12小题)
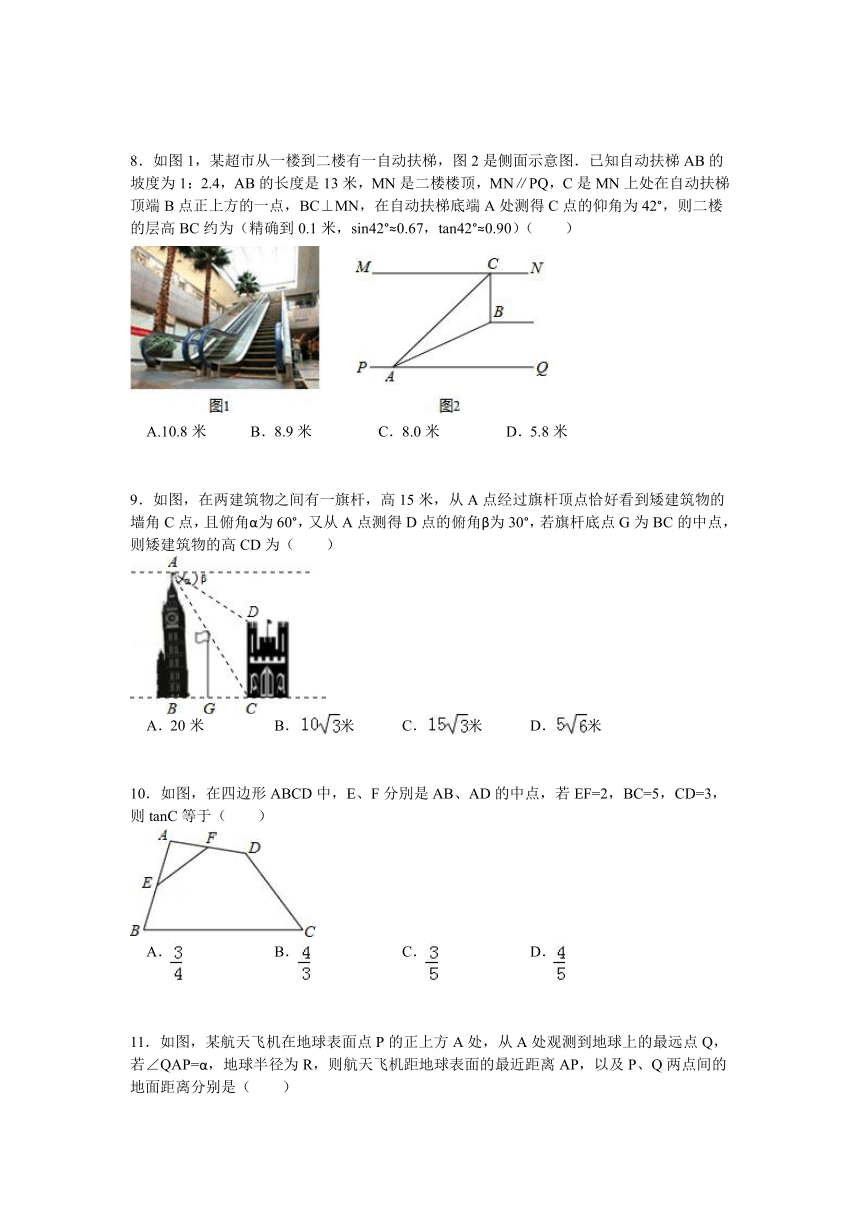
1.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
2.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A. 2 B. C. D.
3.如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
A. ①② B. ②③ C. ①②③ D. ①③
4.如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
A. B. ﹣1 C. 2﹣ D.
5.如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A. (11﹣2)米 B. (11﹣2)米 C. (11﹣2)米 D. (11﹣4)米
6.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是( )
A. 144cm B. 180cm C. 240cm D. 360cm
7.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
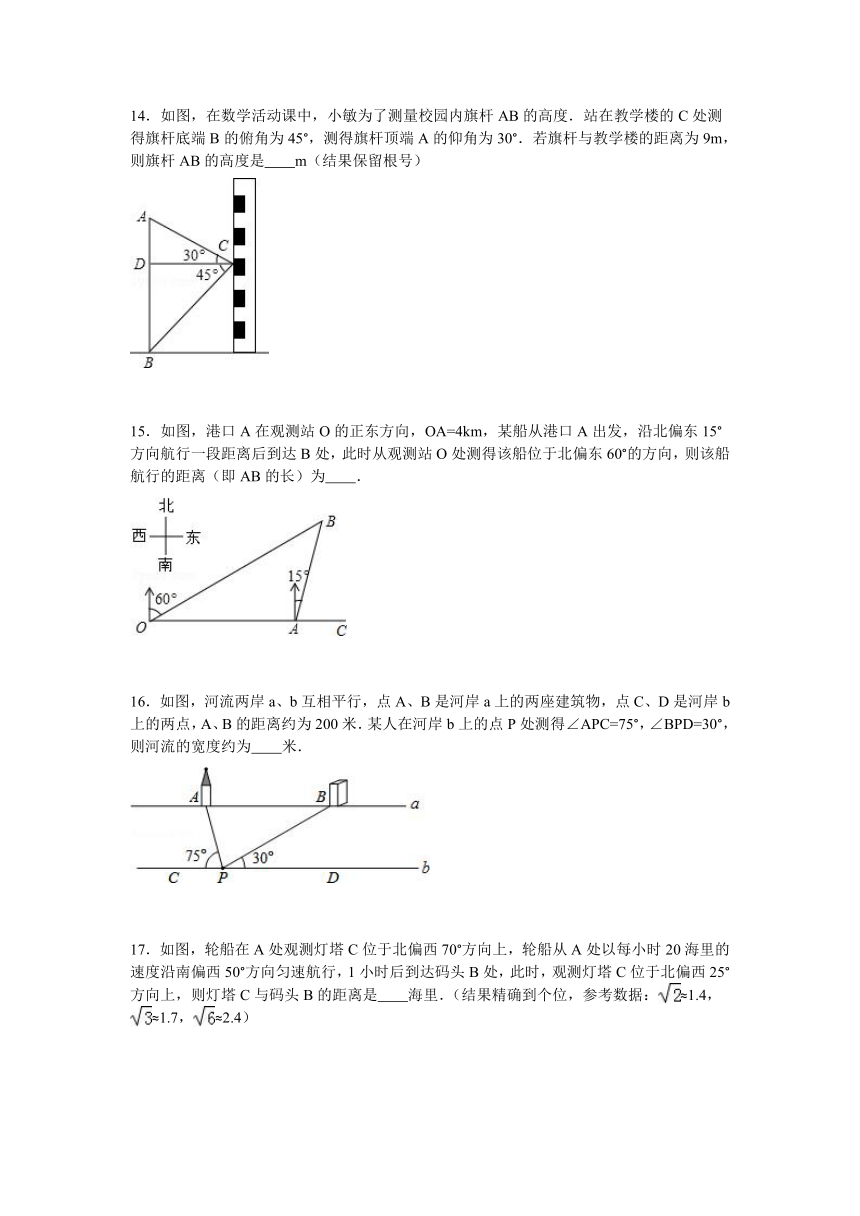
8.如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
A.10.8米 B. 8.9米 C. 8.0米 D. 5.8米
9.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A. 20米 B. 米 C. 米 D. 米
10.如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A. B. C. D.
11.如图,某航天飞机在地球表面点P的正上方A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
A. B.
C. D.
12.如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8cm(如箭头所示),则木桩上升了( )
A. 8tan20° B. C. 8sin20° D. 8cos20°
二.填空题(共8小题)
13.观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
14.如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是 m(结果保留根号)
15.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
16.如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为 米.
17.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)
18.如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD= 米(结果可保留根号)
19.如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线OC将△COA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为 .
20.如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则tan∠A′BC′的值为 .
三.解答题(共10小题)
21.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
22.如图,∠AOB=30°,过OA上到点O的距离为1,3,5,7,…的点作OA的垂线,分别与OB相交,得到图所示的阴影梯形,它们的面积依次记为S1,S2,S3….则
(1)S1= ;
(2)通过计算可得S2009= 5356 .
23.如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
24.钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.
25.如图,某公司入口处有一斜坡AB,坡角为12°,AB的长为3m,施工队准备将斜坡修成三级台阶,台阶高度均为hcm,深度均为30cm,设台阶的起点为C.
(1)求AC的长度;
(2)求每级台阶的高度h.
(参考数据:sin12°≈0.2079,cos12°≈0.9781,tan12°≈0.2126.结果都精确到0.1cm)
26.观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则,即AD=csinB,AD=bsinC,于是csinB=bsinC,即,同理有:,
所以.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.
(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= 60° ;AC= 20 ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,)
27.九年级甲班数学兴趣小组组织社会实践活动,目的是测量一山坡的护坡石坝高度及石坝与地面的倾角∠α.
(1)如图1,小明所在的小组用一根木条EF斜靠在护坡石坝上,使得BF与BE的长度相等,如果测量得到∠EFB=36°,那么∠α的度数是 72° ;
(2)如图2,小亮所在的小组把一根长为5米的竹竿AG斜靠在石坝旁,量出竿长1米时离地面的高度为0.6米,请你求出护坡石坝的垂直高度AH;
(3)全班总结了各组的方法后,设计了如图3方案:在护坡石坝顶部的影子处立一根长为a米的杆子PD,杆子与地面垂直,测得杆子的影子长为b米,点P到护坡石坝底部B的距离为c米,如果利用(1)得到的结论,请你用a、b、c表示出护坡石坝的垂直高度AH.
(sin72°≈0.95,cos72°≈0.3,tan72°≈3)
28.如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据:≈1.41,≈1.73,≈2.24,≈2.45)
参考答案
一.选择题(共12小题)
1.C.
2.D
3.D
4.A
5.D
6.B
7.C
8.D
9.A
10.B
11.B
12.A
二.填空题(共8小题)
13. 135 m.
14.3+9.
15. 2 .
16. 100 .
17. 24
18. 21+7
19. .
20. .
三.解答题(共10小题)
21.解:作PE⊥OB于点E,PF⊥CO于点F, 在Rt△AOC中,AO=100,∠CAO=60°, ∴CO=AO tan60°=100(米). 设PE=x米, ∵tan∠PAB==, ∴AE=2x. 在Rt△PCF中,∠CPF=45°,CF=100﹣x,PF=OA+AE=100+2x, ∵PF=CF, ∴100+2x=100﹣x, 解得x=(米). 答:电视塔OC高为100米,点P的铅直高度为(米).
22.解:(1)设阴影梯形的上底和下底距点O的长分别为a和b, 则上底长为btan∠AOB,下底长为atan∠AOB, ∴Sn=b×btan∠AOB﹣a×atan∠AOB=(b2﹣a2), 又∵梯形1距离点O的距离a=1,b=3, ∴S1=(32﹣12)=; (2)第2009个梯形前面已有2008×2个奇数, 2009个梯形上底距点O的距离为第2008×2+1个奇数, 下底为第2008×2+2个奇数, ∴第2009个梯形的两边长分别为: a=2×(2008×2+1)﹣1=8033, b=2×(2008×2+1)+1=8035, 故S2009=(80352﹣80332)=5356. 故答案为,5356.
23.解:如图:延长AB. ∵CD∥AB, ∴∠CAB=30°,∠CBF=60°; ∴∠BCA=60°﹣30°=30°,即∠BAC=∠BCA; ∴BC=AB=3米; Rt△BCF中,BC=3米,∠CBF=60°; ∴BF=BC=1.5米; 故x=BF﹣EF=1.5﹣0.8=0.7米. 答:这时汽车车头与斑马线的距离x是0.7米.
24.解:在直角△ACM,∠CAM=45度,则△ACM是等腰直角三角形, 则AC=CM=12(海里), ∴BC=AC﹣AB=12﹣4=8(海里), 直角△BCN中,CN=BC tan∠CBN=BC=8(海里), ∴MN=CN﹣CM=8﹣12(海里). 答:钓鱼岛东西两端点MN之间的距离是(8﹣12)海里.
25.解:如右图,过点B作BE⊥AC于点E, (1)在Rt△ABE中,AB=3m,cos12°≈0.9781, AE=ABcos12°≈2.934m=293.4cm, ∴AC=AE﹣CE=293.4﹣60=233.4cm. 答:AC的长度约为233.4cm. (2)h=BE=ABsin12°=×300×0.2079=20.79≈20.8cm. 答:每级台阶的高度h约为20.8cm.
26.解:(1)由正玄定理得:∠A=60°,AC=20; 故答案为:60°,20; (2)如图,依题意:BC=40×0.5=20(海里) ∵CD∥BE,∴∠DCB+∠CBE=180°. ∵∠DCB=30°,∴∠CBE=150°. ∵∠ABE=75°,∴∠ABC=75°. ∴∠A=45°. 在△ABC中,, 即, 解之得:AB=10≈24.49海里. 所以渔政204船距钓鱼岛A的距离约为24.49海里.
27.解:(1)∵BF=BE. ∴∠BFE=∠FEB. ∴∠α=2∠EFB=72°. (2)∵竿长1米时离地面的高度为0.6米,MN∥AH. ∴AG:AH=1:0.6 ∴AH=3米. (3)在Rt△ABH中,BH=AH÷tan72°=AH÷3=. 由题意知,△CPD∽△PHA. ∴DP:CP=AH:PH=AH:(PB+BH)=AH:(PB+). 即:a:b=AH:(c+). 解得:AH=.
28.解:(1)如图,作AD⊥BC于点D. Rt△ABD中, AD=ABsin45°=4×=2. 在Rt△ACD中, ∵∠ACD=30°, ∴AC=2AD=4≈5.6. 即新传送带AC的长度约为5.6米; (2)结论:货物MNQP应挪走. 解:在Rt△ABD中,BD=ABcos45°=4×=2. 在Rt△ACD中,CD=ACcos30°=2. ∴CB=CD﹣BD=2﹣2=2(﹣)≈2.1. ∵PC=PB﹣CB≈4﹣2.1=1.9<2, ∴货物MNQP应挪走.
一.选择题(共12小题)
1.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
2.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A. 2 B. C. D.
3.如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
A. ①② B. ②③ C. ①②③ D. ①③
4.如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )
A. B. ﹣1 C. 2﹣ D.
5.如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A. (11﹣2)米 B. (11﹣2)米 C. (11﹣2)米 D. (11﹣4)米
6.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是( )
A. 144cm B. 180cm C. 240cm D. 360cm
7.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
8.如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
A.10.8米 B. 8.9米 C. 8.0米 D. 5.8米
9.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A. 20米 B. 米 C. 米 D. 米
10.如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A. B. C. D.
11.如图,某航天飞机在地球表面点P的正上方A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
A. B.
C. D.
12.如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8cm(如箭头所示),则木桩上升了( )
A. 8tan20° B. C. 8sin20° D. 8cos20°
二.填空题(共8小题)
13.观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
14.如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是 m(结果保留根号)
15.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
16.如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为 米.
17.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)
18.如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD= 米(结果可保留根号)
19.如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线OC将△COA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为 .
20.如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则tan∠A′BC′的值为 .
三.解答题(共10小题)
21.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)
22.如图,∠AOB=30°,过OA上到点O的距离为1,3,5,7,…的点作OA的垂线,分别与OB相交,得到图所示的阴影梯形,它们的面积依次记为S1,S2,S3….则
(1)S1= ;
(2)通过计算可得S2009= 5356 .
23.如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
24.钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.
25.如图,某公司入口处有一斜坡AB,坡角为12°,AB的长为3m,施工队准备将斜坡修成三级台阶,台阶高度均为hcm,深度均为30cm,设台阶的起点为C.
(1)求AC的长度;
(2)求每级台阶的高度h.
(参考数据:sin12°≈0.2079,cos12°≈0.9781,tan12°≈0.2126.结果都精确到0.1cm)
26.观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则,即AD=csinB,AD=bsinC,于是csinB=bsinC,即,同理有:,
所以.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.
(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= 60° ;AC= 20 ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,)
27.九年级甲班数学兴趣小组组织社会实践活动,目的是测量一山坡的护坡石坝高度及石坝与地面的倾角∠α.
(1)如图1,小明所在的小组用一根木条EF斜靠在护坡石坝上,使得BF与BE的长度相等,如果测量得到∠EFB=36°,那么∠α的度数是 72° ;
(2)如图2,小亮所在的小组把一根长为5米的竹竿AG斜靠在石坝旁,量出竿长1米时离地面的高度为0.6米,请你求出护坡石坝的垂直高度AH;
(3)全班总结了各组的方法后,设计了如图3方案:在护坡石坝顶部的影子处立一根长为a米的杆子PD,杆子与地面垂直,测得杆子的影子长为b米,点P到护坡石坝底部B的距离为c米,如果利用(1)得到的结论,请你用a、b、c表示出护坡石坝的垂直高度AH.
(sin72°≈0.95,cos72°≈0.3,tan72°≈3)
28.如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据:≈1.41,≈1.73,≈2.24,≈2.45)
参考答案
一.选择题(共12小题)
1.C.
2.D
3.D
4.A
5.D
6.B
7.C
8.D
9.A
10.B
11.B
12.A
二.填空题(共8小题)
13. 135 m.
14.3+9.
15. 2 .
16. 100 .
17. 24
18. 21+7
19. .
20. .
三.解答题(共10小题)
21.解:作PE⊥OB于点E,PF⊥CO于点F, 在Rt△AOC中,AO=100,∠CAO=60°, ∴CO=AO tan60°=100(米). 设PE=x米, ∵tan∠PAB==, ∴AE=2x. 在Rt△PCF中,∠CPF=45°,CF=100﹣x,PF=OA+AE=100+2x, ∵PF=CF, ∴100+2x=100﹣x, 解得x=(米). 答:电视塔OC高为100米,点P的铅直高度为(米).
22.解:(1)设阴影梯形的上底和下底距点O的长分别为a和b, 则上底长为btan∠AOB,下底长为atan∠AOB, ∴Sn=b×btan∠AOB﹣a×atan∠AOB=(b2﹣a2), 又∵梯形1距离点O的距离a=1,b=3, ∴S1=(32﹣12)=; (2)第2009个梯形前面已有2008×2个奇数, 2009个梯形上底距点O的距离为第2008×2+1个奇数, 下底为第2008×2+2个奇数, ∴第2009个梯形的两边长分别为: a=2×(2008×2+1)﹣1=8033, b=2×(2008×2+1)+1=8035, 故S2009=(80352﹣80332)=5356. 故答案为,5356.
23.解:如图:延长AB. ∵CD∥AB, ∴∠CAB=30°,∠CBF=60°; ∴∠BCA=60°﹣30°=30°,即∠BAC=∠BCA; ∴BC=AB=3米; Rt△BCF中,BC=3米,∠CBF=60°; ∴BF=BC=1.5米; 故x=BF﹣EF=1.5﹣0.8=0.7米. 答:这时汽车车头与斑马线的距离x是0.7米.
24.解:在直角△ACM,∠CAM=45度,则△ACM是等腰直角三角形, 则AC=CM=12(海里), ∴BC=AC﹣AB=12﹣4=8(海里), 直角△BCN中,CN=BC tan∠CBN=BC=8(海里), ∴MN=CN﹣CM=8﹣12(海里). 答:钓鱼岛东西两端点MN之间的距离是(8﹣12)海里.
25.解:如右图,过点B作BE⊥AC于点E, (1)在Rt△ABE中,AB=3m,cos12°≈0.9781, AE=ABcos12°≈2.934m=293.4cm, ∴AC=AE﹣CE=293.4﹣60=233.4cm. 答:AC的长度约为233.4cm. (2)h=BE=ABsin12°=×300×0.2079=20.79≈20.8cm. 答:每级台阶的高度h约为20.8cm.
26.解:(1)由正玄定理得:∠A=60°,AC=20; 故答案为:60°,20; (2)如图,依题意:BC=40×0.5=20(海里) ∵CD∥BE,∴∠DCB+∠CBE=180°. ∵∠DCB=30°,∴∠CBE=150°. ∵∠ABE=75°,∴∠ABC=75°. ∴∠A=45°. 在△ABC中,, 即, 解之得:AB=10≈24.49海里. 所以渔政204船距钓鱼岛A的距离约为24.49海里.
27.解:(1)∵BF=BE. ∴∠BFE=∠FEB. ∴∠α=2∠EFB=72°. (2)∵竿长1米时离地面的高度为0.6米,MN∥AH. ∴AG:AH=1:0.6 ∴AH=3米. (3)在Rt△ABH中,BH=AH÷tan72°=AH÷3=. 由题意知,△CPD∽△PHA. ∴DP:CP=AH:PH=AH:(PB+BH)=AH:(PB+). 即:a:b=AH:(c+). 解得:AH=.
28.解:(1)如图,作AD⊥BC于点D. Rt△ABD中, AD=ABsin45°=4×=2. 在Rt△ACD中, ∵∠ACD=30°, ∴AC=2AD=4≈5.6. 即新传送带AC的长度约为5.6米; (2)结论:货物MNQP应挪走. 解:在Rt△ABD中,BD=ABcos45°=4×=2. 在Rt△ACD中,CD=ACcos30°=2. ∴CB=CD﹣BD=2﹣2=2(﹣)≈2.1. ∵PC=PB﹣CB≈4﹣2.1=1.9<2, ∴货物MNQP应挪走.
