数学：第1章《算法例题

课件20张PPT。 算法例题选
例1 交换两个变量A和B的值
算法
第一步:输入A,B,
第二步:令x=A,
第三步:令A=B,
第四步:令B=x,
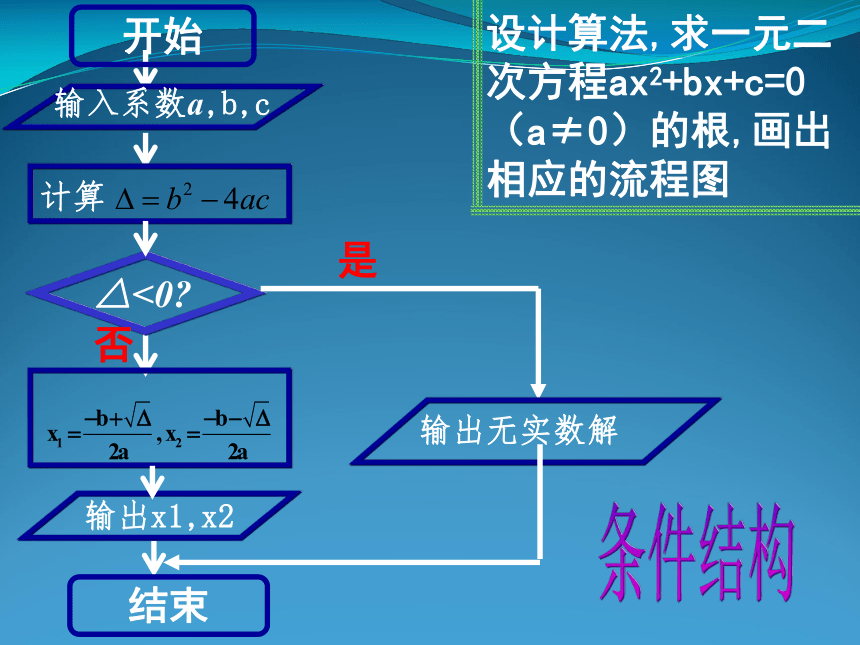
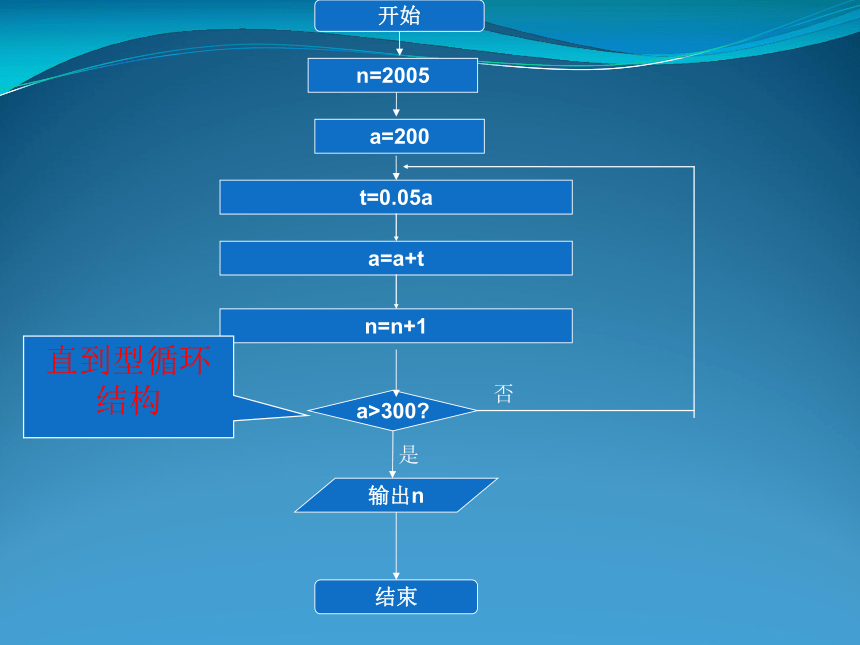
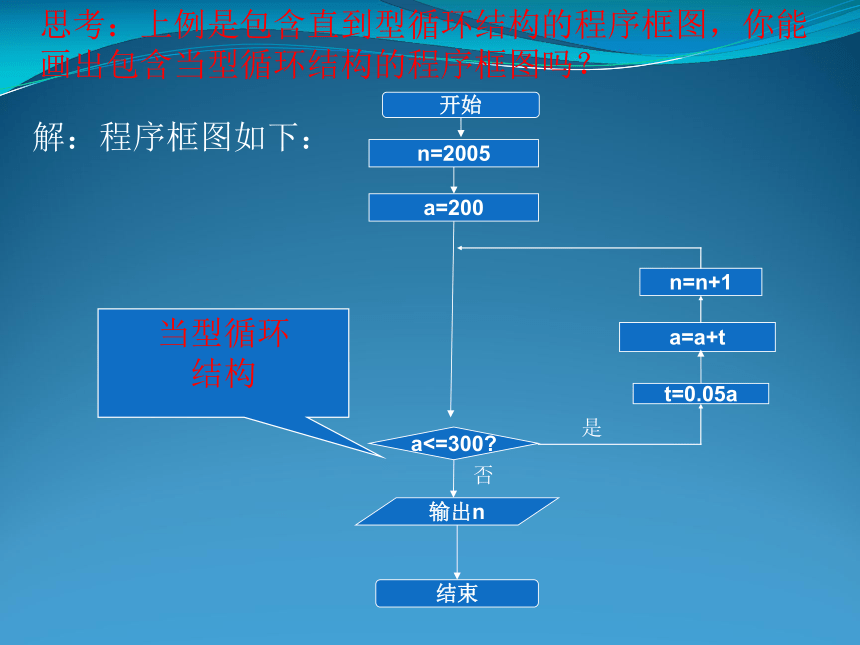
第五步:输出A,B.程序框图:开始B=x输出A,B结束A=Bx=A输入A,B设计算法,求一元二次方程ax2+bx+c=0（ ）的根,画出相应的流程图 a≠0输出x1,x2输入系数a,b,c否是输出无实数解条件结构开始结束例3. 某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5%.设计一程序框图,输出预计年生产总值超过300万元的最早年份。算法分析：1、先写出解决本例的算法步骤：第一步：输入2005年的年生产总值；第二步：计算下一年的年生产总值；第三步：判断所得的结果是否大于300。若是，则输出该年的年份；否则，返回第二步。2、再画出程序框图如下：开始t=0.05aa=a+ta>300?输出n结束否是a=200n=2005n=n+1直到型循环结构思考：上例是包含直到型循环结构的程序框图，你能画出包含当型循环结构的程序框图吗？解：程序框图如下：当型循环
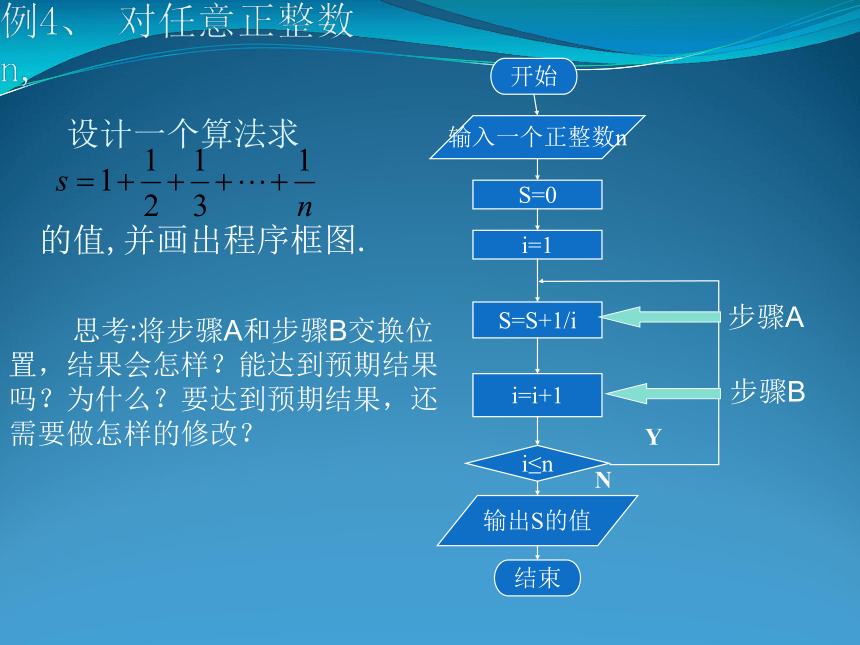
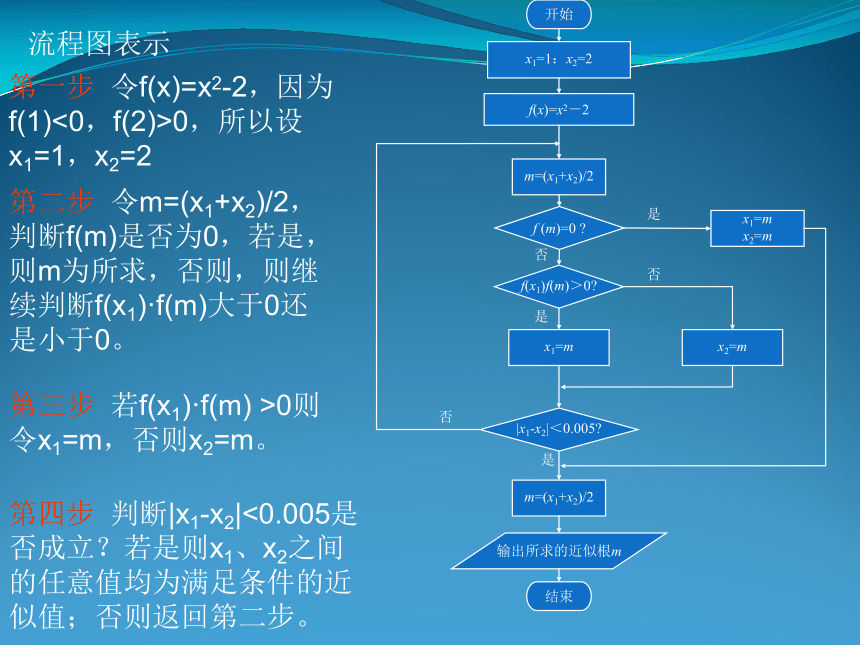
结构 例4、 对任意正整数n,的值,并画出程序框图.开始输入一个正整数n输出S的值结束S=0i=1S=S+1/ii=i+1i≤nYN设计一个算法求 思考:将步骤A和步骤B交换位置，结果会怎样？能达到预期结果吗？为什么？要达到预期结果，还需要做怎样的修改？例5 用二分法求解方程求关于x的方程x2－2＝0的根，精确到0.005算法描述第一步 令f(x)=x2-2，因为f(1)<0，f(2)>0，所以设x1=1，x2=2第二步 令m=(x1+x2)/2，判断f(m)是否为0，若是，则m为所求，否则，则继续判断f(x1)·f(m)大于0还是小于0。第三步 若f(x1)·f(m) >0则令x1=m，否则x2=m。第四步 判断|x1-x2|<0.005是否成立？若是则x1、x2之间的任意值均为满足条件的近似值；否则返回第二步。流程图表示开始输出min结束min=a输入a,b,cb(1).s=0; (2).i=1;
(3).s=s+i;(4).i=i+2;
(5).如果i小于等于31,返回重新执行第3步,第4步,第5步,否则结束,得到s值,s=1+3+5+7+……+31.第二次循环s=第三次循环s=4+5=9
…..s=1+3+5+…+31
初值s=0, i=10+1=1第一次循环s=,i=31+3=4i>31?开始s=0 i=1输出s 结束s=s+i i=i+2否是10、设计一个算法框图：求满足1＋2 ＋ 3 ＋ … ＋ n＞22的最小正整数n，并写出相应的QBASIC程序。区别在哪？例11（P20练习）：设计一个用有理指数幂逼近无理指数幂5　
　　的算法，并估计5　　的近似值，画出算法的程序框图。解：算法步骤如下：第一步：给定精确度d，令i=1；第二步：取出　　的到小数点后第i位的不足近似值，记为a; 取出　　的到小数点后第i位的过剩近似值，记为b；第三步：计算m=5b-5a；第四步：若m