数学:3.4-1《互斥事件》课件(苏教必修3)
文档属性
| 名称 | 数学:3.4-1《互斥事件》课件(苏教必修3) |  | |
| 格式 | rar | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:23:00 | ||
图片预览




文档简介
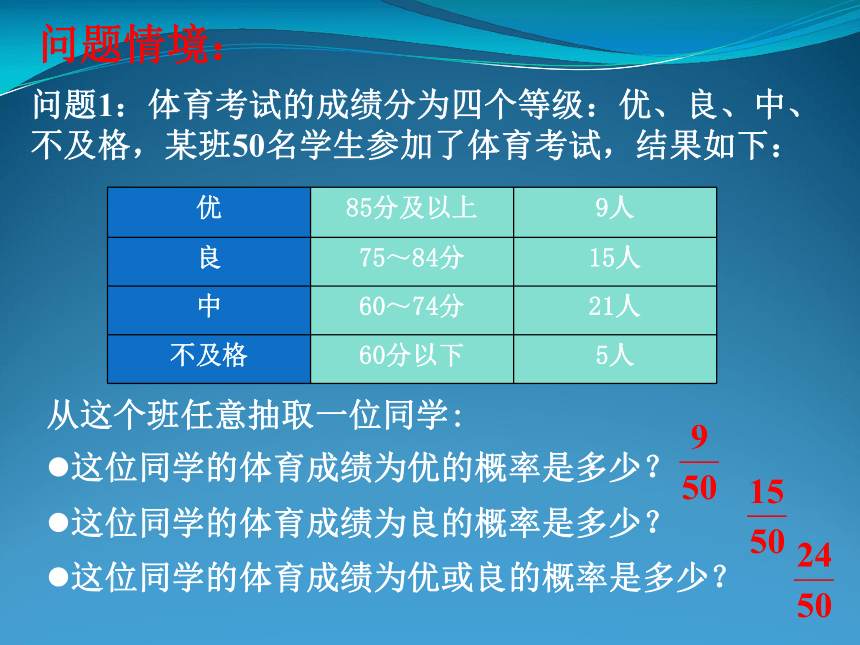
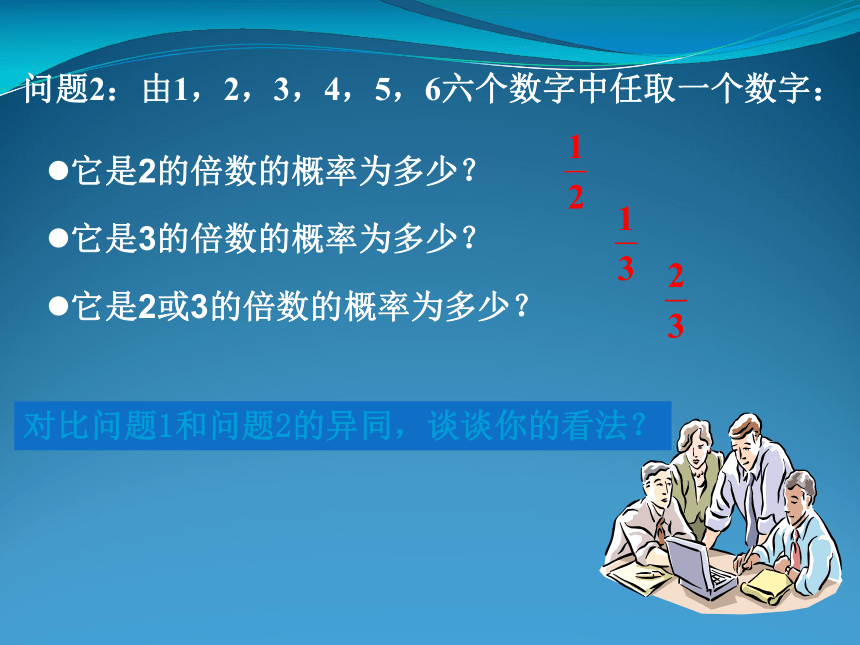
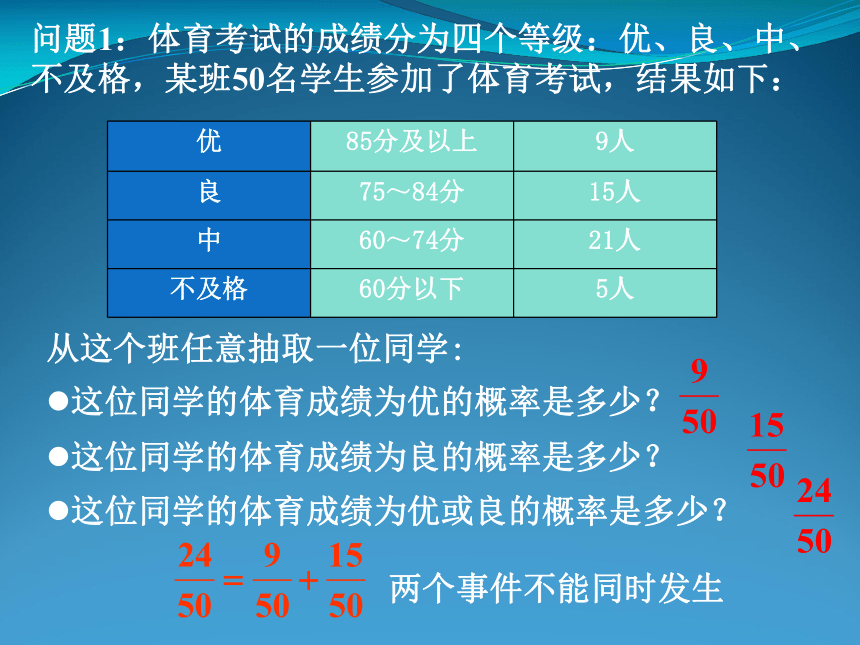
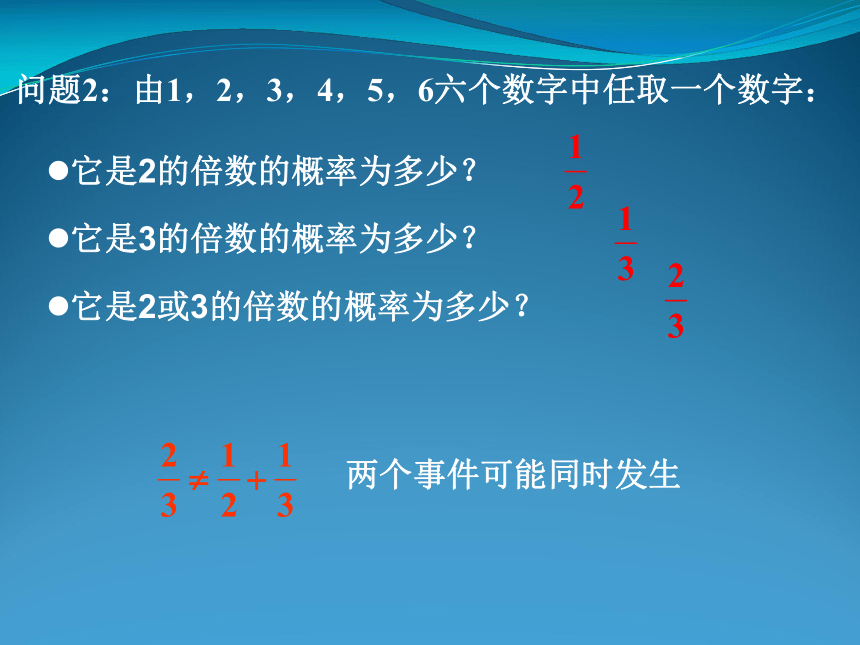
课件20张PPT。互斥事件(1)问题情境:问题1:体育考试的成绩分为四个等级:优、良、中、不及格,某班50名学生参加了体育考试,结果如下:从这个班任意抽取一位同学:这位同学的体育成绩为优的概率是多少?这位同学的体育成绩为良的概率是多少?这位同学的体育成绩为优或良的概率是多少?问题2:由1,2,3,4,5,6六个数字中任取一个数字:它是2的倍数的概率为多少?它是3的倍数的概率为多少?它是2或3的倍数的概率为多少?对比问题1和问题2的异同,谈谈你的看法?问题1:体育考试的成绩分为四个等级:优、良、中、不及格,某班50名学生参加了体育考试,结果如下:从这个班任意抽取一位同学:这位同学的体育成绩为优的概率是多少?这位同学的体育成绩为良的概率是多少?这位同学的体育成绩为优或良的概率是多少?两个事件不能同时发生问题2:由1,2,3,4,5,6六个数字中任取一个数字:它是2的倍数的概率为多少?它是3的倍数的概率为多少?它是2或3的倍数的概率为多少?两个事件可能同时发生不可能同时发生的两个事件叫做互斥事件一副牌共54张,去掉王共有52张,任意抽取一张牌,
事件A:抽取一张牌,得到红桃;
事件B:抽取一张牌,得到黑桃;
事件C:抽取一张牌,得到方片;
事件D:抽取一张牌,得到梅花.问题3:研究下列问题中,各个事件间是否为互斥事件: 从装有4只红球、4只白球的黑袋中任意取出3只球,
记事件A:取出3只红球;
记事件B:取出2只红球和1只白球;
记事件C:取出1只红球和2只白球;
记事件D:取出3只球中至少有1只白球.
指出上列事件中哪些是互斥事件? 哪些不是?试一试:数学理论:互斥事件:不可能同时发生的两个事件叫做互斥事件.彼此互斥:一般地,如果事件A1、 A2、 … An中的任何两个都是互斥的,那么就说事件A1、 A2、 … An彼此互斥.事件A+B:事件A、B有一个发生.
A,B为互斥事件,则P(A+B)=P(A) + P(B)事件A1 + A2 + … + An :事件A1、A2 、… 、 An 有一个发生. A1、 A2 、 … 、 An 彼此互斥,则
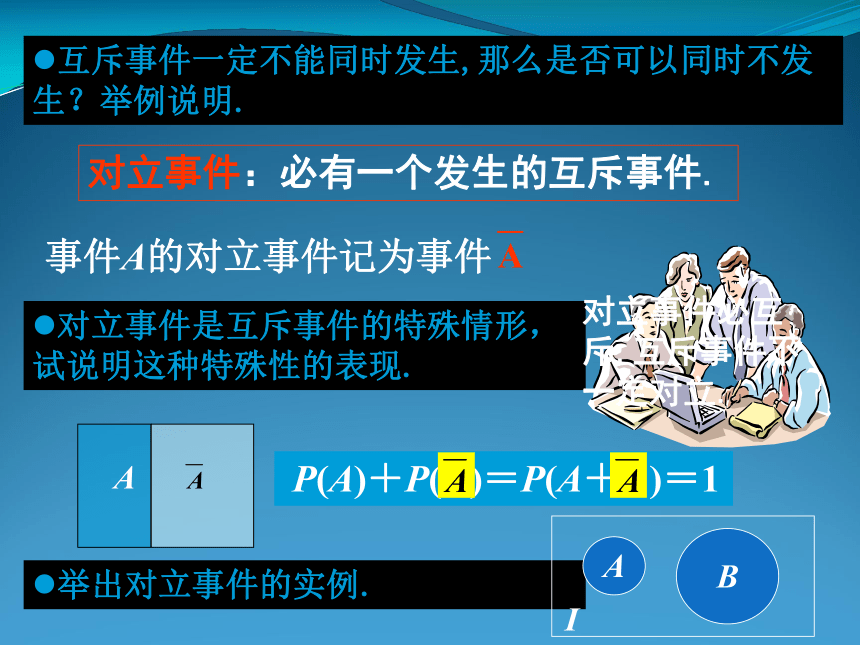
P(A1 + A2 + … + An )=P(A1) + P(A2) + …+ P(An) 互斥事件一定不能同时发生,那么是否可以同时不发生?举例说明.对立事件:必有一个发生的互斥事件.对立事件是互斥事件的特殊情形,试说明这种特殊性的表现.举出对立事件的实例.对立事件必互斥,互斥事件不一定对立.例1 判断下列给出的每对事件,⑴是否为互斥事件,⑵是否为对立事件,并说明理由.
从40张扑克牌(红桃、黑桃、方块、梅花点数从1—10各10张)中,任取一张,(Ⅰ)“抽出红桃”与“抽出黑桃”;(Ⅱ)“抽出红色牌”与“抽出黑色牌”;(Ⅲ)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”.答案:(Ⅰ)是互斥事件,不是对立事件;
(Ⅱ)既是互斥事件,又是对立事件;
(Ⅲ)不是互斥事件,当然不是对立事件.数学运用:例2 从装有4只红球、4只白球的黑袋中任意取出3只球,
记事件A:取出3只红球;
记事件B:取出2只红球和1只白球;
记事件C:取出1只红球和2只白球;
记事件D:取出3只球中至少有1只白球.
指出上列事件中哪些是对立事件? 例3 有10名学生,其中4名男生,6名女生,从中任选2名,求恰好是2名男生或2名女生的概率.解:记“从中任选2名,恰好是2名男生”为事件A, “从中任选2名,恰好是2名女生”为事件B,
则事件A与事件B为互斥事件,且“从中任选2名,恰好是2名男生或2名女生”为事件A+B.答:从中任选2名,恰好是2名男生或2名女生的概率为7/15.例4 在某一时期内,一条河流某处的年最高水位在各个范围内的概率如下:
计算在同一时期内,河流这一处的年最高水位在下列范围内的概率:
(1)[10,16)(m);
(2)[8,12)(m);
(3)[10,18)(m) .在求某些稍复杂的事件的概率时,通常有两种方法:一是将所求事件的概率化成一些彼此互斥的事件的概率的和,二是先去求此事件的对立事件的概率.练一练1、判别下列每对事件是不是互斥事件,如果是,再判别它们是不是对立事件。
从一堆产品(其中正品与次品都多于2个)中任取2件,其中:
(1)恰有1件次品和恰有2件次品; (2)至少有1件次品和全是次品; (3)至少有1件正品和至少有1件次品; (4)至少有1件次品和全是正品。2、抛掷一个骰子,记A为事件“落地时向上的数是奇数”,B为事件“落地时向上的数是偶数”,C为事件“落地时向上的数是3的倍数”
判别下列每件事件是不是互斥事件,如果是,再判别它们是不是对立事件。
(1)A与B;(2)A与C;(3)B与C.3、从1,2,3,4,5,6,7,8,9这九个数字中任取两个数,分别有下列事件,其中为互斥事件的是( ) ①恰有一个奇数和恰有一个偶数,②至少有一个是奇数和两个都是奇数,③至少有一个是奇数和两个都是偶数,④至少有一个是奇数和至少有一个是偶数.
A . ① B . ②④ C . ③ D . ①③C 4、 判断下列说法是否正确: (2)甲、乙两射手同时射击一目标,甲的命中率为0.3,乙的命中率为0.5,则目标被命中的概率等于0.3+0.5=0.8.(1) 一个新手在很远处命中靶的内圈的概率是0.3,则命中靶的其余部分的概率是0.7.错误.因为甲命中目标与乙命中目标两个事件不互斥.错误.因为命中靶的内圈和命中靶的其余部分这两件事虽然是互斥,但不对立.5、 某人射击1次,命中率如下表所示:求射击1次,至少命中7环的概率为_____.0.10.9回顾小结:一、本节课主要应掌握如下知识:
⑴ 互斥事件、对立事件的概念及它们的关系;⑵ n 个彼此互斥事件的概率公式:⑶ 对立事件的概率之和等于1,即:回顾小结:二、在求某些复杂事件(如“至多、至少”的概率时,通常有两种方法:
1、将所求事件的概率化为若干互斥事件的概率的和;
2、求此事件的对立事件的概率.课后作业:课本 P108 习题3.4
No.1、2、3、4.
事件A:抽取一张牌,得到红桃;
事件B:抽取一张牌,得到黑桃;
事件C:抽取一张牌,得到方片;
事件D:抽取一张牌,得到梅花.问题3:研究下列问题中,各个事件间是否为互斥事件: 从装有4只红球、4只白球的黑袋中任意取出3只球,
记事件A:取出3只红球;
记事件B:取出2只红球和1只白球;
记事件C:取出1只红球和2只白球;
记事件D:取出3只球中至少有1只白球.
指出上列事件中哪些是互斥事件? 哪些不是?试一试:数学理论:互斥事件:不可能同时发生的两个事件叫做互斥事件.彼此互斥:一般地,如果事件A1、 A2、 … An中的任何两个都是互斥的,那么就说事件A1、 A2、 … An彼此互斥.事件A+B:事件A、B有一个发生.
A,B为互斥事件,则P(A+B)=P(A) + P(B)事件A1 + A2 + … + An :事件A1、A2 、… 、 An 有一个发生. A1、 A2 、 … 、 An 彼此互斥,则
P(A1 + A2 + … + An )=P(A1) + P(A2) + …+ P(An) 互斥事件一定不能同时发生,那么是否可以同时不发生?举例说明.对立事件:必有一个发生的互斥事件.对立事件是互斥事件的特殊情形,试说明这种特殊性的表现.举出对立事件的实例.对立事件必互斥,互斥事件不一定对立.例1 判断下列给出的每对事件,⑴是否为互斥事件,⑵是否为对立事件,并说明理由.
从40张扑克牌(红桃、黑桃、方块、梅花点数从1—10各10张)中,任取一张,(Ⅰ)“抽出红桃”与“抽出黑桃”;(Ⅱ)“抽出红色牌”与“抽出黑色牌”;(Ⅲ)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”.答案:(Ⅰ)是互斥事件,不是对立事件;
(Ⅱ)既是互斥事件,又是对立事件;
(Ⅲ)不是互斥事件,当然不是对立事件.数学运用:例2 从装有4只红球、4只白球的黑袋中任意取出3只球,
记事件A:取出3只红球;
记事件B:取出2只红球和1只白球;
记事件C:取出1只红球和2只白球;
记事件D:取出3只球中至少有1只白球.
指出上列事件中哪些是对立事件? 例3 有10名学生,其中4名男生,6名女生,从中任选2名,求恰好是2名男生或2名女生的概率.解:记“从中任选2名,恰好是2名男生”为事件A, “从中任选2名,恰好是2名女生”为事件B,
则事件A与事件B为互斥事件,且“从中任选2名,恰好是2名男生或2名女生”为事件A+B.答:从中任选2名,恰好是2名男生或2名女生的概率为7/15.例4 在某一时期内,一条河流某处的年最高水位在各个范围内的概率如下:
计算在同一时期内,河流这一处的年最高水位在下列范围内的概率:
(1)[10,16)(m);
(2)[8,12)(m);
(3)[10,18)(m) .在求某些稍复杂的事件的概率时,通常有两种方法:一是将所求事件的概率化成一些彼此互斥的事件的概率的和,二是先去求此事件的对立事件的概率.练一练1、判别下列每对事件是不是互斥事件,如果是,再判别它们是不是对立事件。
从一堆产品(其中正品与次品都多于2个)中任取2件,其中:
(1)恰有1件次品和恰有2件次品; (2)至少有1件次品和全是次品; (3)至少有1件正品和至少有1件次品; (4)至少有1件次品和全是正品。2、抛掷一个骰子,记A为事件“落地时向上的数是奇数”,B为事件“落地时向上的数是偶数”,C为事件“落地时向上的数是3的倍数”
判别下列每件事件是不是互斥事件,如果是,再判别它们是不是对立事件。
(1)A与B;(2)A与C;(3)B与C.3、从1,2,3,4,5,6,7,8,9这九个数字中任取两个数,分别有下列事件,其中为互斥事件的是( ) ①恰有一个奇数和恰有一个偶数,②至少有一个是奇数和两个都是奇数,③至少有一个是奇数和两个都是偶数,④至少有一个是奇数和至少有一个是偶数.
A . ① B . ②④ C . ③ D . ①③C 4、 判断下列说法是否正确: (2)甲、乙两射手同时射击一目标,甲的命中率为0.3,乙的命中率为0.5,则目标被命中的概率等于0.3+0.5=0.8.(1) 一个新手在很远处命中靶的内圈的概率是0.3,则命中靶的其余部分的概率是0.7.错误.因为甲命中目标与乙命中目标两个事件不互斥.错误.因为命中靶的内圈和命中靶的其余部分这两件事虽然是互斥,但不对立.5、 某人射击1次,命中率如下表所示:求射击1次,至少命中7环的概率为_____.0.10.9回顾小结:一、本节课主要应掌握如下知识:
⑴ 互斥事件、对立事件的概念及它们的关系;⑵ n 个彼此互斥事件的概率公式:⑶ 对立事件的概率之和等于1,即:回顾小结:二、在求某些复杂事件(如“至多、至少”的概率时,通常有两种方法:
1、将所求事件的概率化为若干互斥事件的概率的和;
2、求此事件的对立事件的概率.课后作业:课本 P108 习题3.4
No.1、2、3、4.
