上海市东昌中学2023-2024学年高二下学期期中考试数学试题(含答案)
文档属性
| 名称 | 上海市东昌中学2023-2024学年高二下学期期中考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 704.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 15:05:00 | ||
图片预览




文档简介
东昌中学2023学年第二学期高二年级数学期中
2024.05
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.已知直线,和平面,若,,则与的位置关系是______.
2.已知圆锥的底面半径和高均为1,则该圆锥的表面积为______.
3.若将一个边长为1的正方形围成一个圆柱,则该圆柱的体积为______.
4.如图,水平放置的的斜二测直观图是图中的,若,,则边的实际长度为______.
(第4题) (第8题) (第10题)
5.某学校师生共有3600人,现用分层抽样方法抽取一个容量为240的样本,已知样本中教师人数为30人,则该校学生人数为______.
6.若圆锥的侧面展开图是一个半圆,则该圆锥的母线与轴的夹角大小为______.
7.如果直线与平面所成的角为,那么直线与平面内的直线所成的角的取值范围是______.
8.下图为甲、乙两名篮球运动员每场比赛得分情况的茎叶图,则甲、乙两名篮球运动员得分的中位数的和是______.
9.已知,则______.
10.圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是______cm.
11.现有甲、乙、丙三位同学合作在一个正二十面体(如图)的各面写上0~9这10个数字(相对的两个面上的数字相同),这样就得到一个产生0~9的随机数的骰子.依次投掷这个骰子,并逐个记下朝上一面的数字,就能按顺序排成一个随机数表,若甲、乙、丙依次投掷一次,按顺序记下三个数,三个数恰好构成等差数列的概率为______.
(第11题) (第12题)
12.已知正四面体的棱长为,现截去四个全等的小正四面体,得到如图的八面体,若这个八面体能放进半径为的球形容器中,则截去的小正四面体的棱长最小值为______.
二、单选题(本大题共4题,满分18分,第13-14题每题4分,第15-16题每题5分)
13.设、是两条不同的直线,、是两个不同的平面,则下列命题正确的是( )
A.若,,则 B.若,则
C.若,,则 D.若,,则
14.下列说法正确的个数( )
(1)三点确定一个平面;(2)一条直线和一个点确定一个平面;
(3)两条直线确定一个平面;(4)三角形和梯形一定为平面图形.
A.0 B.1 C.2 D.3
15.下列命题中成立的是( )
A.各个面都是三角形的多面体一定是棱锥
B.有两个相邻侧面是矩形的棱柱是直棱柱
C.一个棱锥的侧面是全等的等腰三角形,那它一定是正棱锥
D.各个侧面都是矩形的棱柱是长方体
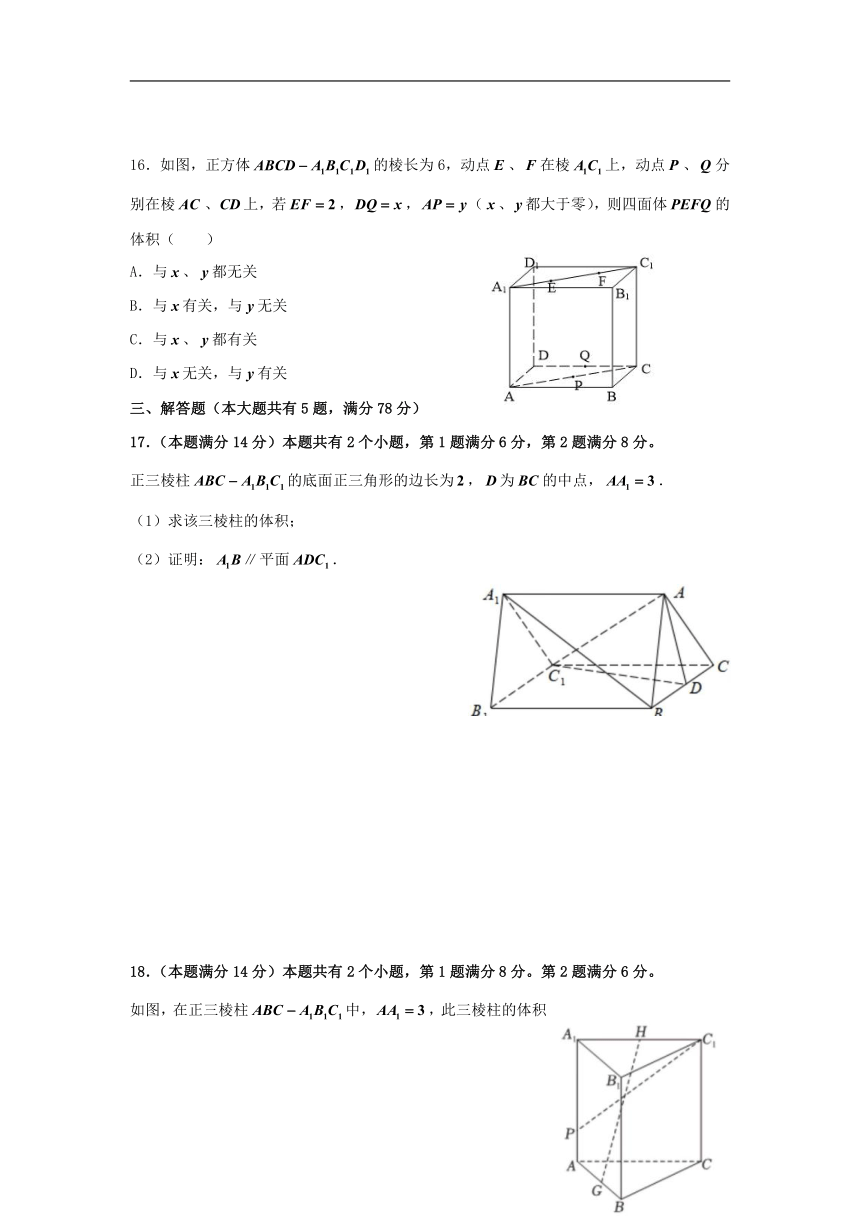
16.如图,正方体的棱长为6,动点、在棱上,动点、分别在棱、上,若,,(、都大于零),则四面体的体积( )
A.与、都无关
B.与有关,与无关
C.与、都有关
D.与无关,与有关
三、解答题(本大题共有5题,满分78分)
17.(本题满分14分)本题共有2个小题,第1题满分6分,第2题满分8分。
正三棱柱的底面正三角形的边长为,为的中点,.
(1)求该三棱柱的体积;
(2)证明:平面.
18.(本题满分14分)本题共有2个小题,第1题满分8分。第2题满分6分。
如图,在正三棱柱中,,此三棱柱的体积为,为侧棱上点,且,、分别为、的中点.
(1)求异面直线与所成角的大小;
(2)求与平面所成角的大小.
19.(本题满分14分)本题共有2个小题,第1题满分8分,第2题满分6分。
已知四棱锥的底面为直角梯形,,,平面,且,是棱上的动点.
(1)若,求点到平面的距离;
(2)当是中点时,求以为直径的球被平面所截的截面面积.
20.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
如图,已知椭圆,左顶点为,经过点,过点作斜率为的直线交椭圆于点,交轴于点.
(1)求椭圆的方程;
(2)已知为的中点,,证明:对于任意的都有恒成立;
(3)若过点作直线的平行线交椭圆于点,求的最小值.
21.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
已知函数(、).
(1)当,时,求函数图象在点的切线方程;
(2)当时,既存在极大值,又存在极小值,求实数的取值范围;
(3)当,时,,分别为的极大值点和极小值点,且,求实数的取值范围.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11. 12.
12.已知正四面体的棱长为,现截去四个全等的小正四面体,得到如图的八面体,若这个八面体能放进半径为的球形容器中,则截去的小正四面体的棱长最小值为______.
【答案】
【解析】如图, 取上下底面的中心分别为, 外接球的心为,连接,,
设截去的小正四面体的棱长为, 八面体外接的半径截角四面体外接球的球心是原正四面体外接球的球心,原正四面体的棱长为, 则外接球的半径湤足,即, 可得,
又,,解得:.
截去的小正四面体的棱长最小值为.故答案为:.
二、选择题
13. C 14.B 15. B 16.B
15.下列命题中成立的是( )
A.各个面都是三角形的多面体一定是棱锥
B.有两个相邻侧面是矩形的棱柱是直棱柱
C.一个棱锥的侧面是全等的等腰三角形,那它一定是正棱锥
D.各个侧面都是矩形的棱柱是长方体
【答案】B
【解析】对, 只要将底面全等的两个棱锥的底面重合在一起,
所得多面体的每个面都是三角形, 但这个多面体不是棱锥, 如图, 故错误;
对, 若棱柱有两个相邻侧面是矩形, 则侧棱与底面两条相交的边垂直,
则侧棱与底面垂直, 此时棱柱一定是直棱柱, 故正确;
对于, 如图所示, 若
满足侧面均为全等的等腰三角形, 但此时底面不是正三角形, 故错误;
对, 各个侧面都是矩形的棱柱不一定是长方体,比如底面为三角形的直三棱柱, 故错误.
故选:.
三.解答题
17.(1) (2)证明略
18.(1) (2)
19.(1) (2)
20.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
如图,已知椭圆,左顶点为,经过点,过点作斜率为的直线交椭圆于点,交轴于点.
(1)求椭圆的方程;
(2)已知为的中点,,证明:对于任意的都有恒成立;
(3)若过点作直线的平行线交椭圆于点,求的最小值.
【答案】(1) (2)见解析 (3)
【解析】(1)已知椭圆, 左顶点为, 经过点
椭圆方程为:.
(2) 设直线的方程,交轴于点,
联立, 得
,
对于任意的都有恒成立.
(3),的方程可设为:,
由, 得点横坐标为
由, 得
当且仅当, 即时取等号,
当时,的最小值为
21.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
已知函数(、).
(1)当,时,求函数图象在点的切线方程;
(2)当时,既存在极大值,又存在极小值,求实数的取值范围;
(3)当,时,,分别为的极大值点和极小值点,且,求实数的取值范围.
【答案】(1) (2) (3)
【解析】(1) 已知、), 函数定义域为,
当时,,可得,此时,易知,
所以函数过点的切线方程为,即为;
(2)当时,
可得
因为函数既存在极大值, 又存在极小值,所以必有两个不等的实根,
此时,令,解得或, 且,所以且;
不妨考虑当的情况下,
当时,单调递增; 当时,单调递减;
当时,单调递增,
所以函数分别在取得极大值和极小值, 满足条件,
当的情况下,
当时,单调递增; 当时,单调递减;
当时,单调递增,所以函数分别在取得极大值和极小值, 满足条件,
综上, 实数的取值范围为;
(3) 当时,由 (2) 得..
当时,单调递增; 当时,单调递减;
当时,单调递增,所以在处取得极大值;
在取得极小值,
因为恒成立,
所以对任意的恒成立,此时,
则,所以,整理得,
不妨设, 函数定义域为,
可得
令方程,可得,
当, 即时,单调递增;
所以,即, 符合条件;
当, 即时,设方程的两个根分别为,
可得,不妨设,
当时,单调递减,
所以当时,,即, 不符合条件;
综上, 实数的取值范围为.
2024.05
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.已知直线,和平面,若,,则与的位置关系是______.
2.已知圆锥的底面半径和高均为1,则该圆锥的表面积为______.
3.若将一个边长为1的正方形围成一个圆柱,则该圆柱的体积为______.
4.如图,水平放置的的斜二测直观图是图中的,若,,则边的实际长度为______.
(第4题) (第8题) (第10题)
5.某学校师生共有3600人,现用分层抽样方法抽取一个容量为240的样本,已知样本中教师人数为30人,则该校学生人数为______.
6.若圆锥的侧面展开图是一个半圆,则该圆锥的母线与轴的夹角大小为______.
7.如果直线与平面所成的角为,那么直线与平面内的直线所成的角的取值范围是______.
8.下图为甲、乙两名篮球运动员每场比赛得分情况的茎叶图,则甲、乙两名篮球运动员得分的中位数的和是______.
9.已知,则______.
10.圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是______cm.
11.现有甲、乙、丙三位同学合作在一个正二十面体(如图)的各面写上0~9这10个数字(相对的两个面上的数字相同),这样就得到一个产生0~9的随机数的骰子.依次投掷这个骰子,并逐个记下朝上一面的数字,就能按顺序排成一个随机数表,若甲、乙、丙依次投掷一次,按顺序记下三个数,三个数恰好构成等差数列的概率为______.
(第11题) (第12题)
12.已知正四面体的棱长为,现截去四个全等的小正四面体,得到如图的八面体,若这个八面体能放进半径为的球形容器中,则截去的小正四面体的棱长最小值为______.
二、单选题(本大题共4题,满分18分,第13-14题每题4分,第15-16题每题5分)
13.设、是两条不同的直线,、是两个不同的平面,则下列命题正确的是( )
A.若,,则 B.若,则
C.若,,则 D.若,,则
14.下列说法正确的个数( )
(1)三点确定一个平面;(2)一条直线和一个点确定一个平面;
(3)两条直线确定一个平面;(4)三角形和梯形一定为平面图形.
A.0 B.1 C.2 D.3
15.下列命题中成立的是( )
A.各个面都是三角形的多面体一定是棱锥
B.有两个相邻侧面是矩形的棱柱是直棱柱
C.一个棱锥的侧面是全等的等腰三角形,那它一定是正棱锥
D.各个侧面都是矩形的棱柱是长方体
16.如图,正方体的棱长为6,动点、在棱上,动点、分别在棱、上,若,,(、都大于零),则四面体的体积( )
A.与、都无关
B.与有关,与无关
C.与、都有关
D.与无关,与有关
三、解答题(本大题共有5题,满分78分)
17.(本题满分14分)本题共有2个小题,第1题满分6分,第2题满分8分。
正三棱柱的底面正三角形的边长为,为的中点,.
(1)求该三棱柱的体积;
(2)证明:平面.
18.(本题满分14分)本题共有2个小题,第1题满分8分。第2题满分6分。
如图,在正三棱柱中,,此三棱柱的体积为,为侧棱上点,且,、分别为、的中点.
(1)求异面直线与所成角的大小;
(2)求与平面所成角的大小.
19.(本题满分14分)本题共有2个小题,第1题满分8分,第2题满分6分。
已知四棱锥的底面为直角梯形,,,平面,且,是棱上的动点.
(1)若,求点到平面的距离;
(2)当是中点时,求以为直径的球被平面所截的截面面积.
20.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
如图,已知椭圆,左顶点为,经过点,过点作斜率为的直线交椭圆于点,交轴于点.
(1)求椭圆的方程;
(2)已知为的中点,,证明:对于任意的都有恒成立;
(3)若过点作直线的平行线交椭圆于点,求的最小值.
21.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
已知函数(、).
(1)当,时,求函数图象在点的切线方程;
(2)当时,既存在极大值,又存在极小值,求实数的取值范围;
(3)当,时,,分别为的极大值点和极小值点,且,求实数的取值范围.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11. 12.
12.已知正四面体的棱长为,现截去四个全等的小正四面体,得到如图的八面体,若这个八面体能放进半径为的球形容器中,则截去的小正四面体的棱长最小值为______.
【答案】
【解析】如图, 取上下底面的中心分别为, 外接球的心为,连接,,
设截去的小正四面体的棱长为, 八面体外接的半径截角四面体外接球的球心是原正四面体外接球的球心,原正四面体的棱长为, 则外接球的半径湤足,即, 可得,
又,,解得:.
截去的小正四面体的棱长最小值为.故答案为:.
二、选择题
13. C 14.B 15. B 16.B
15.下列命题中成立的是( )
A.各个面都是三角形的多面体一定是棱锥
B.有两个相邻侧面是矩形的棱柱是直棱柱
C.一个棱锥的侧面是全等的等腰三角形,那它一定是正棱锥
D.各个侧面都是矩形的棱柱是长方体
【答案】B
【解析】对, 只要将底面全等的两个棱锥的底面重合在一起,
所得多面体的每个面都是三角形, 但这个多面体不是棱锥, 如图, 故错误;
对, 若棱柱有两个相邻侧面是矩形, 则侧棱与底面两条相交的边垂直,
则侧棱与底面垂直, 此时棱柱一定是直棱柱, 故正确;
对于, 如图所示, 若
满足侧面均为全等的等腰三角形, 但此时底面不是正三角形, 故错误;
对, 各个侧面都是矩形的棱柱不一定是长方体,比如底面为三角形的直三棱柱, 故错误.
故选:.
三.解答题
17.(1) (2)证明略
18.(1) (2)
19.(1) (2)
20.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
如图,已知椭圆,左顶点为,经过点,过点作斜率为的直线交椭圆于点,交轴于点.
(1)求椭圆的方程;
(2)已知为的中点,,证明:对于任意的都有恒成立;
(3)若过点作直线的平行线交椭圆于点,求的最小值.
【答案】(1) (2)见解析 (3)
【解析】(1)已知椭圆, 左顶点为, 经过点
椭圆方程为:.
(2) 设直线的方程,交轴于点,
联立, 得
,
对于任意的都有恒成立.
(3),的方程可设为:,
由, 得点横坐标为
由, 得
当且仅当, 即时取等号,
当时,的最小值为
21.(本题满分18分)本题共有3个小题,第1题满分4分,第2题满分6分,第3题满分8分。
已知函数(、).
(1)当,时,求函数图象在点的切线方程;
(2)当时,既存在极大值,又存在极小值,求实数的取值范围;
(3)当,时,,分别为的极大值点和极小值点,且,求实数的取值范围.
【答案】(1) (2) (3)
【解析】(1) 已知、), 函数定义域为,
当时,,可得,此时,易知,
所以函数过点的切线方程为,即为;
(2)当时,
可得
因为函数既存在极大值, 又存在极小值,所以必有两个不等的实根,
此时,令,解得或, 且,所以且;
不妨考虑当的情况下,
当时,单调递增; 当时,单调递减;
当时,单调递增,
所以函数分别在取得极大值和极小值, 满足条件,
当的情况下,
当时,单调递增; 当时,单调递减;
当时,单调递增,所以函数分别在取得极大值和极小值, 满足条件,
综上, 实数的取值范围为;
(3) 当时,由 (2) 得..
当时,单调递增; 当时,单调递减;
当时,单调递增,所以在处取得极大值;
在取得极小值,
因为恒成立,
所以对任意的恒成立,此时,
则,所以,整理得,
不妨设, 函数定义域为,
可得
令方程,可得,
当, 即时,单调递增;
所以,即, 符合条件;
当, 即时,设方程的两个根分别为,
可得,不妨设,
当时,单调递减,
所以当时,,即, 不符合条件;
综上, 实数的取值范围为.
同课章节目录
