沪教版七年级数学下册试题 15.2直角坐标平面内点的运动(含解析)
文档属性
| 名称 | 沪教版七年级数学下册试题 15.2直角坐标平面内点的运动(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 738.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 21:21:09 | ||
图片预览




文档简介
15.2直角坐标平面内点的运动
一、单选题
1.与平面直角坐标系中的点具有一一对应关系的是( )
A.实数 B.有理数
C.有序实数对 D.有序有理数对
2.已知点在轴上,则点的坐标是( )
A. B. C. D.
3.如图是在方格纸上画出的小旗图案,如果用表示点,表示点,那么点的位置可表示为( )
A. B. C. D.
4.如果在y轴上,那么点P的坐标是
A. B. C. D.
5.在平面直角坐标系中,点在第四象限,它到轴和轴的距离分别是2、5,则点的坐标为( )
A. B. C. D.
6.在平面直角坐标系中,点的坐标,点的坐标,将线段平移,使得到达点,点到达点,则点的坐标是( )
A. B. C. D.
二、填空题
7.在平面直角坐标系中,点P(m+3,m+1)在y轴上,则m=_____.
8.已知,点 M 在第四象限,它到 x 轴的距离为 6,到 y 轴的距离为 3,则点 M的坐标为________.
9.若点N到x轴的距离为1,到y轴的距离为2,则点N的坐标为_______.
10.经过点P且垂直于y轴的直线可表示为直线_________.
11.在平面直角坐标系中,的三个顶点分别为、、,点在第一象限,如果与全等,那么点的坐标为__________.
12.在平面直角坐标系中,如果轴,点的坐标为,且,那么点的坐标为__________.
13.在平面直角坐标系中,经过点且垂直于轴的直线可以表示为直线______________.
14.经过点且垂直于轴的直线可以表示为直线_______.
15.在平面直角坐标系中,点的坐标是,若直线平行于轴,且两点距离等于3,则点的坐标为____________.
16.与点关于轴对称的点的横坐标是______.
17.已知点是直角坐标平面内的点,如果,那么点在第________象限.
18.在平面直角坐标系中,线段AB=5,AB∥x轴,若A点坐标为(-1,3),则B点坐标为______.
19.已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是______.
三、解答题
20.如图,在平面直角坐标系中
(1)写出、、三点的坐标:
(______________),(______________),(______________);
(2)的面积为__________________;
(3)若点在轴上,且与的面积相等,则点的坐标为_____________.
21.如图,在直角坐标平面内,已知点A的坐标(-5,0).
(1)写出图中B点的坐标 ;
(2)若点B关于原点对称的点是C,则的面积是 ;
(3)在平面直角坐标系中找一点D,使为等腰直角三角形,且以OB为直角边,则点D的坐标是 .
22.在直角坐标平面内,已知点A(0,5)和点B(-2,4),BC=4, 且BC∥x.
(1)求出点C的坐标;
(2)画出点C的位置,联结AB、AC、BC,判断△ABC的形状,并求出它的面积.
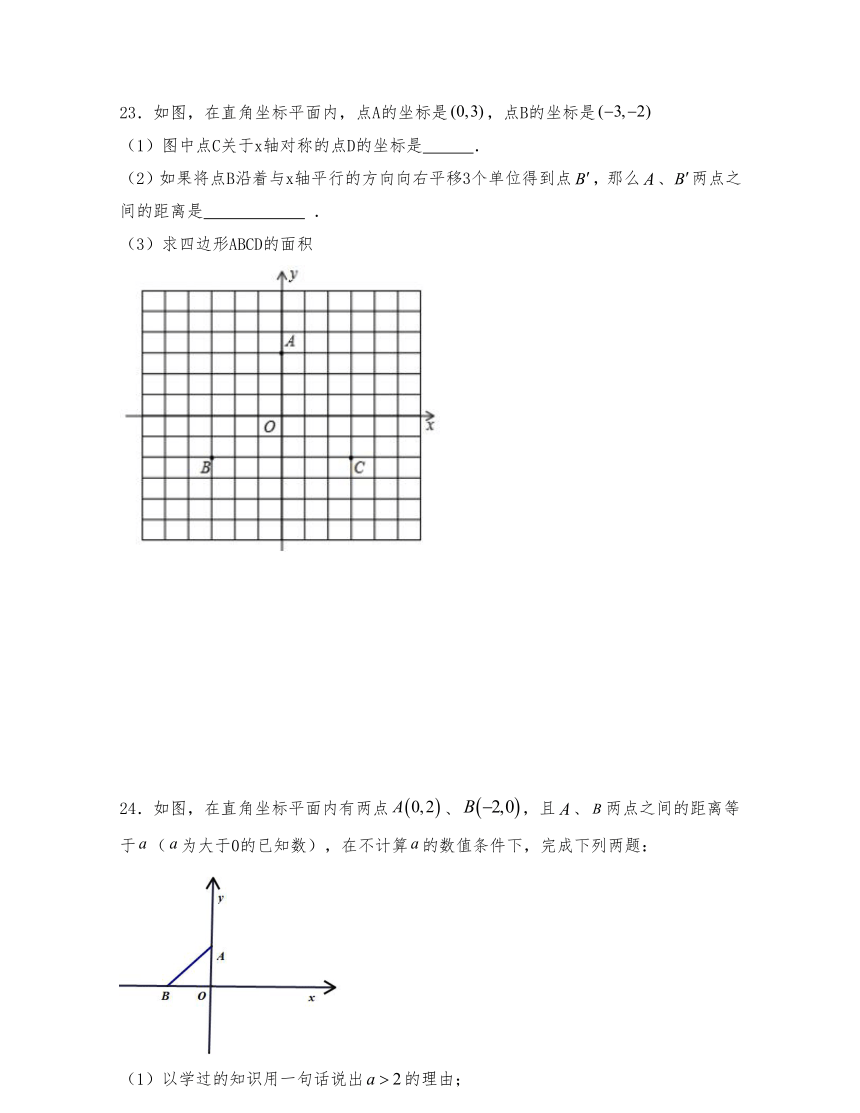
23.如图,在直角坐标平面内,点A的坐标是,点B的坐标是
(1)图中点C关于x轴对称的点D的坐标是 .
(2)如果将点B沿着与x轴平行的方向向右平移3个单位得到点,那么、两点之间的距离是 .
(3)求四边形ABCD的面积
24.如图,在直角坐标平面内有两点、,且、两点之间的距离等于(为大于0的已知数),在不计算的数值条件下,完成下列两题:
(1)以学过的知识用一句话说出的理由;
(2)在轴上是否存在点,使是等腰三角形,如果存在,请写出点的坐标,并求的面积;如果不存在,请说明理由.
25.如图 ,在平面直角坐标系中,直线AB∥ x轴,线段AB与 y 轴交于点M ,已知点 A的坐标是(-2,3), BM4,点C 与点 B 关于 x 轴对称.
(1)在图中描出点C ,并直接写出点 B 和点C 的坐标:B ,C ;
(2)联结 AC 、BC ,AC 与 x 轴交于点 D ,试判断△ABC 的形状,并直接写出点 D的坐标;
(3)在坐标平面内, x 轴的下方,是否存在这样的点 P ,使得△ACP 是等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.
答案
一、单选题
1.C
【分析】根据平面直角坐标系与有序实数对的关系,可得答案
【详解】有序实数对与平面直角坐标系中的点具有一一对应关系,
故选C.
2.B
【分析】根据在x轴上的点的性质求出m的值,即可求出点的坐标.
【详解】∵点在轴上
∴
解得
即
∴点
故答案为:B.
3.D
【分析】根据A点坐标,建立坐标系,可得C点坐标.
【详解】解:如图,以点A为原点建立平面直角坐标系
点C的位置可表示为(3,2),
故选D.
4.B
【分析】根据点在y轴上,可知P的横坐标为0,即可得m的值,再确定点P的坐标即可.
【详解】解:∵在y轴上,∴
解得,
∴点P的坐标是(0,-2).故选B.
5.A
【分析】先根据点B所在的象限确定横纵坐标的符号,然后根据点B与坐标轴的距离得出点B的坐标.
【详解】∵点B在第四象限内,∴点B的横坐标为正数,纵坐标为负数
∵点B到轴和轴的距离分别是2、5
∴横坐标为5,纵坐标为-2
故选:A
6.C
【分析】根据A和C的坐标可得点A向右平移4个单位,向上平移1个单位,点B的平移方法与A的平移方法相同,再根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得点D的坐标.
【详解】解:∵点A(0,1)的对应点C的坐标为(4,2),即(0+4,1+1),
∴点B(3,3)的对应点D的坐标为(3+4,3+1),即D(7,4);
故选:C.
二、填空题
7.﹣3
【分析】由点P在y轴上,得出m+3=0,即可得出答案.
【详解】解:∵点P(m+3,m+1)在y轴上,∴m+3=0,
解得:m=﹣3.故答案为:﹣3.
8.(3,﹣6)
【分析】根据第四象限内的点的坐标特点解答即可.
【详解】解:∵点M在第四象限,到x轴的距离是6,到y轴的距离是3,
∴点M的纵坐标是﹣6,横坐标是3,
即点M的坐标是(3,﹣6),
故答案为:(3,﹣6).
9.(2,1)、(﹣2,1)、(﹣2,﹣1)、(2,﹣1)
【分析】根据点的坐标与其距x、y轴距离的关系得出答案即可
【详解】∵点N到x轴的距离为点N的纵坐标的绝对值
∴点N的纵坐标为±2
∵点N到y轴的距离为点N的横坐标的绝对值
∴点N的横坐标为±1
∴点N的坐标为:(2,1)、(﹣2,1)、(﹣2,﹣1)、(2,﹣1)
故答案为(2,1)、(﹣2,1)、(﹣2,﹣1)、(2,﹣1)
10.y=1
【分析】根据题意画出图形,数形结合即可得出答案.
【详解】如图,
∴经过点且垂直于y轴的直线可表示为直线 ,
故答案为:.
11.或
【分析】存在两种情况,一种是△ABC≌△ABP,另一种是△ABC≌△BAP,分别根据全等的特点画图可得点P的坐标.
【详解】如下图,存在两种情况
情况一:△ABC≌△AB,则点P的坐标为:
情况二:△ABC≌△BA,则点P的坐标为:
故答案为:或
12.或
【分析】存在两种情况,一种是点B在点A的左侧,另一种是点B在点A的右侧,分别根据平行的特点求解可得.
【详解】∵AB∥y轴,∴点A、B的横坐标相同
∴点B的横坐标为:-3
情况一:点B在点A的左侧
∵AB=5,∴点B的纵坐标为4-5=-1
情况二:点B在点A的右侧
∵AB=5,∴点B的纵坐标为4+5=9
故答案为:或
13.
【分析】垂直于y轴的直线表示为:y=m的形式,根据点A的坐标可得m=6.
【详解】∵直线经过点,且垂直于y轴
∴直线表示为:
故答案为:
14.
【分析】根据垂直于坐标轴的直线解析式的形式解答.
【详解】∵经过点P(-1,5)且垂直于x轴,
∴直线的解析式是x=-1.故答案为:x=-1.
15.或
【分析】根据平行于轴的直线上的点纵坐标相等,得出点B的纵坐标为2,再根据两点距离等于3,用A点的横坐标加3或减3即可
【详解】∵点的坐标是,直线平行于轴, ∴B点的纵坐标为2;
∵两点距离等于3,∴B点的横坐标为-3+3=0或-3-3=-6
∴B或故答案为:或
16.
【分析】根据关于轴对称的点的性质求解即可.
【详解】∵某点关于轴对称的点的横坐标等于该点的横坐标
∴与点关于轴对称的点的横坐标为
故答案为:.
17.一、三
【分析】先根据有理数乘法法则得出ab>0时有两种情况,再根据平面直角坐标系中各象限内的点的坐标符号特点即可求解.
【详解】解:∵点M(a,b)是直角坐标平面内的点,若ab>0,
∴a>0,b>0或a<0,b<0.
当a>0,b>0时,M(a,b)在第一象限;
当a<0,b<0时,M(a,b)在第三象限;
故答案为一、三.
18.(4,3)或( 6,3).
【分析】线段AB∥x轴,A、B两点纵坐标相等,又AB=5,B点可能在A点左边或者右边,根据距离确定B点坐标.
【详解】∵AB∥x轴,
∴A、B两点纵坐标都为3,
又∵AB=5,
∴当B点在A点左边时,B(-6,3),
当B点在A点右边时,B(4,3).
故答案为:(4,3)或( 6,3).
19.±4
试题分析:根据坐标与图形得到三角形OAB的两边分别为|a|与5,然后根据三角形面积公式有:,
解得a=4或a=-4,
即a的值为±4.
三、解答题
20.(1)直接读图得:,,
(2)如下图过点A、B、C分别作平行于x轴、y轴的线段
∵,,
∴,,
∴
(3)情况一:如下图,点P在轴的负半轴上
设点P(m,0)
=MC×MN---
=-m×4-×(-m)×2--
=-2m-3
∵与的面积相等
∴-2m-3=
解得m=
∴点
情况二:如下图,点P在轴的正半轴上
=MG×MN---
=(m+3)×4-×m×2--
=2m+3
同理,2m+3=
解得:m=
∴点P
21.(1)由点B在坐标系的位置,可知:B点的坐标(-3,4),
故答案是:(-3,4);
(2)如图1所示:,
故答案是:20;
(3)如图2所示:符合要求点D的坐标为:
.
22.(1) 根据平移的性质x轴右移加,左移减,y轴不变,即可求出C (-6,-4), C (2,-4);
(2)
①根据图象∠ABC1>90°,得出△ABC1是钝角三角形
S△ABC1= BC1×9=×4×9=18
②△ABC是等腰三角形
∵A C1=
A C =
∴△ABC是等腰三角形,
△ABC=×4×9=18
23.解:(1)根据题意,∵点A的坐标是,点B的坐标是
∴点C的坐标为,
∴点C关于x轴对称的点D的坐标是;
故答案为:(3,2);
(2)如图:
将点B沿着与x轴平行的方向向右平移3个单位得到点B′(-3+3,-2),即(0,-2),
∴A、B′两点之间的距离是:3-(-2)=5;
故答案为:5;
(3)四边形ABCD的面积为:
;
24.解:(1)∵在平面直角坐标系中,AO⊥BO,O为垂足,
∴AO表示A点到直线BO的距离,∵,∴,
∵垂线段最短,且不与O重合,
∴,即,
∴的理由是“垂线段最短”;
(2)在轴上存在点,使是等腰三角形,
①如图1,当P在B点左边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
②如图2,当P在B点右边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
③如图3,当P在B点右边,BP=AP,为等腰三角形,
此时P与O重合,即,
∵、,
∴,,
∴;
④如图4,当P在B点右边,AP=AB=a,为等腰三角形,
∵AO⊥BO,
∴O为PB中点,
∴,
∴,,
∴;
综上所述:在轴上存在点,使是等腰三角形,
当,;
当,;
当,;
当,;
25.解:(1)如图,可知点B(4,3),C(4,-3);
(2)如图,
∵B(4,3),
∴AB=6,
∵C(4,-3),BC⊥x轴,
∴BC=6,
∴AB=BC,∠ABC=90,
∴△ABC是等腰直角三角形,
设BC交x轴于点E,则∠DEC=90,OE=4,
∵∠DCE=45,
∴DE=CE=3,
∴OD=OE-DE=4-3=1,
∴D(1,0);
(3))存在点 P,使得△ACP 是等腰直角三角形,如图,
①当∠APC是直角时,P1(-2,-3);
②当∠PAC是直角时,P2(-8,-3);
③当∠PCA是直角时,P3(-2,-9),
故点 P1 (-2,-3)或 P2 (-8,-3)或 P3 (-2,-9).
一、单选题
1.与平面直角坐标系中的点具有一一对应关系的是( )
A.实数 B.有理数
C.有序实数对 D.有序有理数对
2.已知点在轴上,则点的坐标是( )
A. B. C. D.
3.如图是在方格纸上画出的小旗图案,如果用表示点,表示点,那么点的位置可表示为( )
A. B. C. D.
4.如果在y轴上,那么点P的坐标是
A. B. C. D.
5.在平面直角坐标系中,点在第四象限,它到轴和轴的距离分别是2、5,则点的坐标为( )
A. B. C. D.
6.在平面直角坐标系中,点的坐标,点的坐标,将线段平移,使得到达点,点到达点,则点的坐标是( )
A. B. C. D.
二、填空题
7.在平面直角坐标系中,点P(m+3,m+1)在y轴上,则m=_____.
8.已知,点 M 在第四象限,它到 x 轴的距离为 6,到 y 轴的距离为 3,则点 M的坐标为________.
9.若点N到x轴的距离为1,到y轴的距离为2,则点N的坐标为_______.
10.经过点P且垂直于y轴的直线可表示为直线_________.
11.在平面直角坐标系中,的三个顶点分别为、、,点在第一象限,如果与全等,那么点的坐标为__________.
12.在平面直角坐标系中,如果轴,点的坐标为,且,那么点的坐标为__________.
13.在平面直角坐标系中,经过点且垂直于轴的直线可以表示为直线______________.
14.经过点且垂直于轴的直线可以表示为直线_______.
15.在平面直角坐标系中,点的坐标是,若直线平行于轴,且两点距离等于3,则点的坐标为____________.
16.与点关于轴对称的点的横坐标是______.
17.已知点是直角坐标平面内的点,如果,那么点在第________象限.
18.在平面直角坐标系中,线段AB=5,AB∥x轴,若A点坐标为(-1,3),则B点坐标为______.
19.已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是______.
三、解答题
20.如图,在平面直角坐标系中
(1)写出、、三点的坐标:
(______________),(______________),(______________);
(2)的面积为__________________;
(3)若点在轴上,且与的面积相等,则点的坐标为_____________.
21.如图,在直角坐标平面内,已知点A的坐标(-5,0).
(1)写出图中B点的坐标 ;
(2)若点B关于原点对称的点是C,则的面积是 ;
(3)在平面直角坐标系中找一点D,使为等腰直角三角形,且以OB为直角边,则点D的坐标是 .
22.在直角坐标平面内,已知点A(0,5)和点B(-2,4),BC=4, 且BC∥x.
(1)求出点C的坐标;
(2)画出点C的位置,联结AB、AC、BC,判断△ABC的形状,并求出它的面积.
23.如图,在直角坐标平面内,点A的坐标是,点B的坐标是
(1)图中点C关于x轴对称的点D的坐标是 .
(2)如果将点B沿着与x轴平行的方向向右平移3个单位得到点,那么、两点之间的距离是 .
(3)求四边形ABCD的面积
24.如图,在直角坐标平面内有两点、,且、两点之间的距离等于(为大于0的已知数),在不计算的数值条件下,完成下列两题:
(1)以学过的知识用一句话说出的理由;
(2)在轴上是否存在点,使是等腰三角形,如果存在,请写出点的坐标,并求的面积;如果不存在,请说明理由.
25.如图 ,在平面直角坐标系中,直线AB∥ x轴,线段AB与 y 轴交于点M ,已知点 A的坐标是(-2,3), BM4,点C 与点 B 关于 x 轴对称.
(1)在图中描出点C ,并直接写出点 B 和点C 的坐标:B ,C ;
(2)联结 AC 、BC ,AC 与 x 轴交于点 D ,试判断△ABC 的形状,并直接写出点 D的坐标;
(3)在坐标平面内, x 轴的下方,是否存在这样的点 P ,使得△ACP 是等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.
答案
一、单选题
1.C
【分析】根据平面直角坐标系与有序实数对的关系,可得答案
【详解】有序实数对与平面直角坐标系中的点具有一一对应关系,
故选C.
2.B
【分析】根据在x轴上的点的性质求出m的值,即可求出点的坐标.
【详解】∵点在轴上
∴
解得
即
∴点
故答案为:B.
3.D
【分析】根据A点坐标,建立坐标系,可得C点坐标.
【详解】解:如图,以点A为原点建立平面直角坐标系
点C的位置可表示为(3,2),
故选D.
4.B
【分析】根据点在y轴上,可知P的横坐标为0,即可得m的值,再确定点P的坐标即可.
【详解】解:∵在y轴上,∴
解得,
∴点P的坐标是(0,-2).故选B.
5.A
【分析】先根据点B所在的象限确定横纵坐标的符号,然后根据点B与坐标轴的距离得出点B的坐标.
【详解】∵点B在第四象限内,∴点B的横坐标为正数,纵坐标为负数
∵点B到轴和轴的距离分别是2、5
∴横坐标为5,纵坐标为-2
故选:A
6.C
【分析】根据A和C的坐标可得点A向右平移4个单位,向上平移1个单位,点B的平移方法与A的平移方法相同,再根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得点D的坐标.
【详解】解:∵点A(0,1)的对应点C的坐标为(4,2),即(0+4,1+1),
∴点B(3,3)的对应点D的坐标为(3+4,3+1),即D(7,4);
故选:C.
二、填空题
7.﹣3
【分析】由点P在y轴上,得出m+3=0,即可得出答案.
【详解】解:∵点P(m+3,m+1)在y轴上,∴m+3=0,
解得:m=﹣3.故答案为:﹣3.
8.(3,﹣6)
【分析】根据第四象限内的点的坐标特点解答即可.
【详解】解:∵点M在第四象限,到x轴的距离是6,到y轴的距离是3,
∴点M的纵坐标是﹣6,横坐标是3,
即点M的坐标是(3,﹣6),
故答案为:(3,﹣6).
9.(2,1)、(﹣2,1)、(﹣2,﹣1)、(2,﹣1)
【分析】根据点的坐标与其距x、y轴距离的关系得出答案即可
【详解】∵点N到x轴的距离为点N的纵坐标的绝对值
∴点N的纵坐标为±2
∵点N到y轴的距离为点N的横坐标的绝对值
∴点N的横坐标为±1
∴点N的坐标为:(2,1)、(﹣2,1)、(﹣2,﹣1)、(2,﹣1)
故答案为(2,1)、(﹣2,1)、(﹣2,﹣1)、(2,﹣1)
10.y=1
【分析】根据题意画出图形,数形结合即可得出答案.
【详解】如图,
∴经过点且垂直于y轴的直线可表示为直线 ,
故答案为:.
11.或
【分析】存在两种情况,一种是△ABC≌△ABP,另一种是△ABC≌△BAP,分别根据全等的特点画图可得点P的坐标.
【详解】如下图,存在两种情况
情况一:△ABC≌△AB,则点P的坐标为:
情况二:△ABC≌△BA,则点P的坐标为:
故答案为:或
12.或
【分析】存在两种情况,一种是点B在点A的左侧,另一种是点B在点A的右侧,分别根据平行的特点求解可得.
【详解】∵AB∥y轴,∴点A、B的横坐标相同
∴点B的横坐标为:-3
情况一:点B在点A的左侧
∵AB=5,∴点B的纵坐标为4-5=-1
情况二:点B在点A的右侧
∵AB=5,∴点B的纵坐标为4+5=9
故答案为:或
13.
【分析】垂直于y轴的直线表示为:y=m的形式,根据点A的坐标可得m=6.
【详解】∵直线经过点,且垂直于y轴
∴直线表示为:
故答案为:
14.
【分析】根据垂直于坐标轴的直线解析式的形式解答.
【详解】∵经过点P(-1,5)且垂直于x轴,
∴直线的解析式是x=-1.故答案为:x=-1.
15.或
【分析】根据平行于轴的直线上的点纵坐标相等,得出点B的纵坐标为2,再根据两点距离等于3,用A点的横坐标加3或减3即可
【详解】∵点的坐标是,直线平行于轴, ∴B点的纵坐标为2;
∵两点距离等于3,∴B点的横坐标为-3+3=0或-3-3=-6
∴B或故答案为:或
16.
【分析】根据关于轴对称的点的性质求解即可.
【详解】∵某点关于轴对称的点的横坐标等于该点的横坐标
∴与点关于轴对称的点的横坐标为
故答案为:.
17.一、三
【分析】先根据有理数乘法法则得出ab>0时有两种情况,再根据平面直角坐标系中各象限内的点的坐标符号特点即可求解.
【详解】解:∵点M(a,b)是直角坐标平面内的点,若ab>0,
∴a>0,b>0或a<0,b<0.
当a>0,b>0时,M(a,b)在第一象限;
当a<0,b<0时,M(a,b)在第三象限;
故答案为一、三.
18.(4,3)或( 6,3).
【分析】线段AB∥x轴,A、B两点纵坐标相等,又AB=5,B点可能在A点左边或者右边,根据距离确定B点坐标.
【详解】∵AB∥x轴,
∴A、B两点纵坐标都为3,
又∵AB=5,
∴当B点在A点左边时,B(-6,3),
当B点在A点右边时,B(4,3).
故答案为:(4,3)或( 6,3).
19.±4
试题分析:根据坐标与图形得到三角形OAB的两边分别为|a|与5,然后根据三角形面积公式有:,
解得a=4或a=-4,
即a的值为±4.
三、解答题
20.(1)直接读图得:,,
(2)如下图过点A、B、C分别作平行于x轴、y轴的线段
∵,,
∴,,
∴
(3)情况一:如下图,点P在轴的负半轴上
设点P(m,0)
=MC×MN---
=-m×4-×(-m)×2--
=-2m-3
∵与的面积相等
∴-2m-3=
解得m=
∴点
情况二:如下图,点P在轴的正半轴上
=MG×MN---
=(m+3)×4-×m×2--
=2m+3
同理,2m+3=
解得:m=
∴点P
21.(1)由点B在坐标系的位置,可知:B点的坐标(-3,4),
故答案是:(-3,4);
(2)如图1所示:,
故答案是:20;
(3)如图2所示:符合要求点D的坐标为:
.
22.(1) 根据平移的性质x轴右移加,左移减,y轴不变,即可求出C (-6,-4), C (2,-4);
(2)
①根据图象∠ABC1>90°,得出△ABC1是钝角三角形
S△ABC1= BC1×9=×4×9=18
②△ABC是等腰三角形
∵A C1=
A C =
∴△ABC是等腰三角形,
△ABC=×4×9=18
23.解:(1)根据题意,∵点A的坐标是,点B的坐标是
∴点C的坐标为,
∴点C关于x轴对称的点D的坐标是;
故答案为:(3,2);
(2)如图:
将点B沿着与x轴平行的方向向右平移3个单位得到点B′(-3+3,-2),即(0,-2),
∴A、B′两点之间的距离是:3-(-2)=5;
故答案为:5;
(3)四边形ABCD的面积为:
;
24.解:(1)∵在平面直角坐标系中,AO⊥BO,O为垂足,
∴AO表示A点到直线BO的距离,∵,∴,
∵垂线段最短,且不与O重合,
∴,即,
∴的理由是“垂线段最短”;
(2)在轴上存在点,使是等腰三角形,
①如图1,当P在B点左边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
②如图2,当P在B点右边,BP=BA=a,为等腰三角形,
∵,
∴,
∴;
③如图3,当P在B点右边,BP=AP,为等腰三角形,
此时P与O重合,即,
∵、,
∴,,
∴;
④如图4,当P在B点右边,AP=AB=a,为等腰三角形,
∵AO⊥BO,
∴O为PB中点,
∴,
∴,,
∴;
综上所述:在轴上存在点,使是等腰三角形,
当,;
当,;
当,;
当,;
25.解:(1)如图,可知点B(4,3),C(4,-3);
(2)如图,
∵B(4,3),
∴AB=6,
∵C(4,-3),BC⊥x轴,
∴BC=6,
∴AB=BC,∠ABC=90,
∴△ABC是等腰直角三角形,
设BC交x轴于点E,则∠DEC=90,OE=4,
∵∠DCE=45,
∴DE=CE=3,
∴OD=OE-DE=4-3=1,
∴D(1,0);
(3))存在点 P,使得△ACP 是等腰直角三角形,如图,
①当∠APC是直角时,P1(-2,-3);
②当∠PAC是直角时,P2(-8,-3);
③当∠PCA是直角时,P3(-2,-9),
故点 P1 (-2,-3)或 P2 (-8,-3)或 P3 (-2,-9).
