新人教版选择性必修第一册高中物理第4章光真题演练(含解析)
文档属性
| 名称 | 新人教版选择性必修第一册高中物理第4章光真题演练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-05-10 10:04:37 | ||
图片预览




文档简介
第4章 光
一、高考真题探析
典 题 (2022·全国乙卷,34(2))一细束单色光在三棱镜ABC的侧面AC上以大角度由D点入射(入射面在棱镜的横截面内),入射角为i,经折射后射至AB边的E点,如图所示。逐渐减小i,E点向B点移动,当sin i=时,恰好没有光线从AB边射出棱镜,且DE=DA。求棱镜的折射率。
二、临场真题练兵
1.(2023·重庆卷)某实验小组利用双缝干涉实验装置分别观察a、b两单色光的干涉条纹,发现在相同的条件下光屏上a光相邻两亮条纹的间距比b光的小。他们又将a、b光以相同的入射角由水斜射入空气,发现a光的折射角比b光的大,则( D )
A.在空气中传播时,a光的波长比b光的大
B.在水中传播时,a光的速度比b光的大
C.在水中传播时,a光的频率比b光的小
D.由水射向空气时,a光的全反射临界角比b光的小
2.(2023·山东卷)如图所示为一种干涉热膨胀仪原理图。G为标准石英环,C为待测柱形样品,C的上表面与上方标准平面石英板之间存在劈形空气层。用单色平行光垂直照射上方石英板,会形成干涉条纹。已知C的膨胀系数小于G的膨胀系数,当温度升高时,下列说法正确的是( A )
A.劈形空气层的厚度变大,条纹向左移动
B.劈形空气层的厚度变小,条纹向左移动
C.劈形空气层的厚度变大,条纹向右移动
D.劈形空气层的厚度变小,条纹向右移动
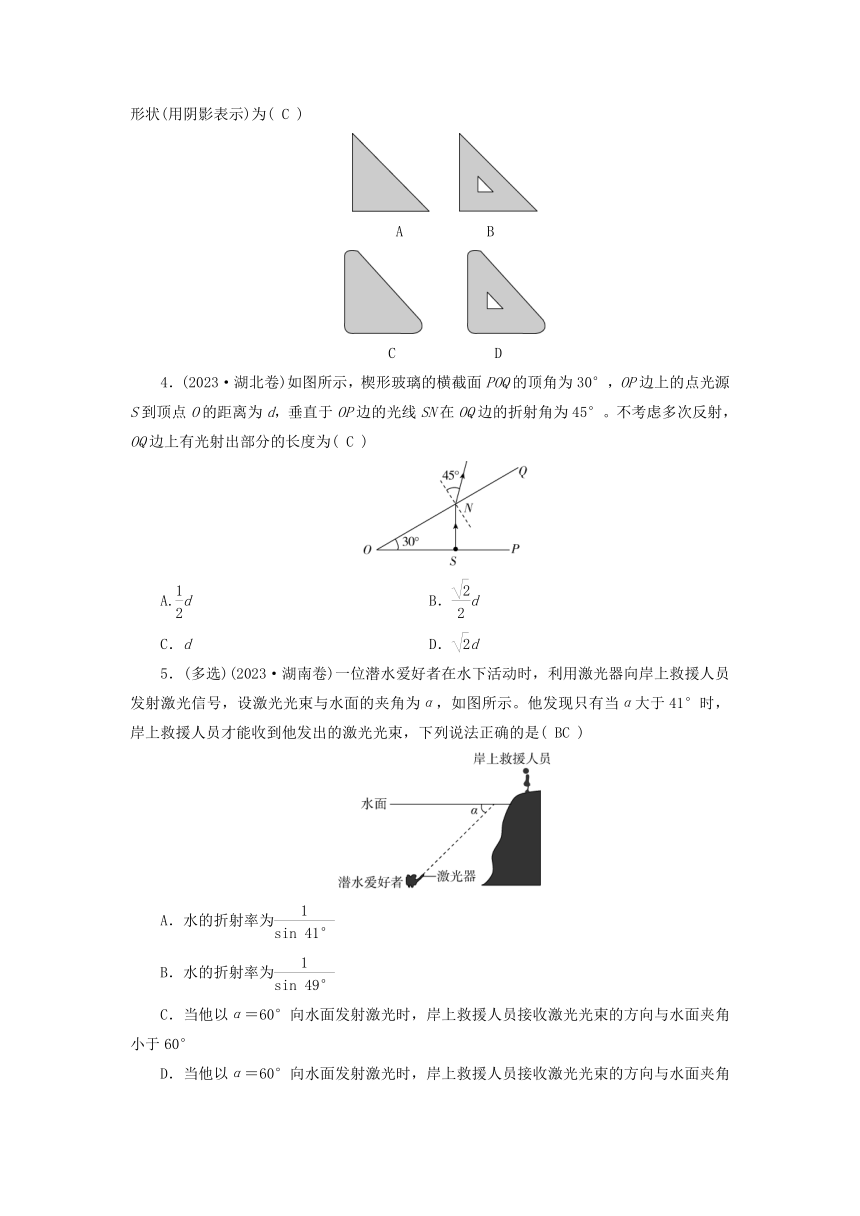
3.(2023·浙江卷)在水池底部水平放置三条细灯带构成的等腰直角三角形发光体,直角边的长度为0.9 m,水的折射率n=,细灯带到水面的距离h= m,则有光射出的水面形状(用阴影表示)为( C )
A B
C D
4.(2023·湖北卷)如图所示,楔形玻璃的横截面POQ的顶角为30°,OP边上的点光源S到顶点O的距离为d,垂直于OP边的光线SN在OQ边的折射角为45°。不考虑多次反射,OQ边上有光射出部分的长度为( C )
A.d B.d
C.d D.d
5.(多选)(2023·湖南卷)一位潜水爱好者在水下活动时,利用激光器向岸上救援人员发射激光信号,设激光光束与水面的夹角为α,如图所示。他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,下列说法正确的是( BC )
A.水的折射率为
B.水的折射率为
C.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角小于60°
D.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角大于60°
6.(多选)(2023·全国卷)等腰三角形△abc为一棱镜的横截面,ab=ac;一平行于bc边的细光束从ab边射入棱镜,在bc边反射后从ac边射出,出射光分成了不同颜色的两束,甲光的出射点在乙光的下方,如图所示。不考虑多次反射。下列说法正确的是( AC )
A.甲光的波长比乙光的长
B.甲光的频率比乙光的高
C.在棱镜中的传播速度,甲光比乙光的大
D.该棱镜对甲光的折射率大于对乙光的折射率
7.(2022·山东卷,7)柱状光学器件横截面如图所示,OP右侧是以O为圆心、半径为R的圆,左侧是直角梯形,AP长为R,AC与CO夹角为45°,AC中点为B。a、b两种频率的细激光束,垂直AB面入射,器件介质对a、b光的折射率分别为1.42、1.40。保持光的入射方向不变,入射点从A向B移动过程中,能在PM面全反射后,从OM面出射的光是(不考虑三次反射以后的光)( A )
A.仅有a光
B.仅有b光
C.a、b光都可以
D.a、b光都不可以
8.(2022·辽宁卷,5)完全失重时,液滴呈球形,气泡在液体中将不会上浮。2021年12月,在中国空间站“天宫课堂”的水球光学实验中,航天员向水球中注入空气形成了一个内含气泡的水球。如图所示,若气泡与水球同心,在过球心O的平面内,用单色平行光照射这一水球,下列说法正确的是( C )
A.此单色光从空气进入水球,频率一定变大
B.此单色光从空气进入水球,频率一定变小
C.若光线1在M处发生全反射,光线2在N处一定发生全反射
D.若光线2在N处发生全反射,光线1在M处一定发生全反射
9.(2021·山东等级考,7)用平行单色光垂直照射一层透明薄膜,观察到如图所示明暗相间的干涉条纹。下列关于该区域薄膜厚度d随坐标x的变化图像,可能正确的是( D )
10.(2023·广东卷)某同学用激光笔和透明长方体玻璃砖测量玻璃的折射率,实验过程如下:
(1)将玻璃砖平放在水平桌面上的白纸上,用大头针在白纸上标记玻璃砖的边界
(2)①激光笔发出的激光从玻璃砖上的M点水平入射,到达ef面上的O点后反射到N点射出。用大头针在白纸上标记O点、M点和激光笔出光孔Q的位置
②移走玻璃砖,在白纸上描绘玻璃砖的边界和激光的光路,作QM连线的延长线与ef面的边界交于P点,如图(a)所示
③用刻度尺测量PM和OM的长度d1和d2。PM的示数如图(b)所示,d1为___。测得d2为3.40 cm。
(3)利用所测量的物理量,写出玻璃砖折射率的表达式n= ;由测得的数据可得折射率n为___(结果保留3位有效数字)
(4)相对误差的计算式为δ=×100%。为了减小d1、d2测量的相对误差,实验中激光在M点入射时应尽量使入射角___。
11.(2023·海南卷)用激光测玻璃砖折射率的实验中,玻璃砖与屏P平行放置,从另一侧用激光笔以一定角度照射,此时在屏上的S1处有激光点,移走玻璃砖,光点移到S2处,回答下列问题:
(1)请画出激光束经玻璃折射后完整的光路图___;
(2)已经测出AB=l1,OA=l2,S1S2=l3,则折射率n= (用l1、l2、l3表示);
(3)若改用宽ab更小的玻璃砖做实验,则S1S2间的距离会___(选填“变大”“变小”或“不变”)。
12.(2021·全国甲卷,34(1))如图,单色光从折射率n=1.5、厚度d=10.0 cm的玻璃板上表面射入。已知真空中的光速为3.0×108 m/s,则该单色光在玻璃板内传播的速度为___m/s;对于所有可能的入射角,该单色光通过玻璃板所用时间t的取值范围是___s≤t< s (不考虑反射)。
13.(2021·浙江6月选考,17(2))如图所示是“用双缝干涉测量光的波长”实验的装置。实验中:
(1)观察到较模糊的干涉条纹,要使条纹变得清晰,值得尝试的是___(单选)。
A.旋转测量头
B.增大单缝与双缝间的距离
C.调节拨杆使单缝与双缝平行
(2)要增大观察到的条纹间距,正确的做法是___(单选)。
A.减小单缝与光源间的距离
B.减小单缝与双缝间的距离
C.增大透镜与单缝间的距离
D.增大双缝与测量头间的距离
14.(2023·山东卷)一种反射式光纤位移传感器可以实现微小位移测量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝M、N,相距为d,直径均为2a,折射率为n(n<)。M、N下端横截面平齐且与被测物体表面平行。激光在M内多次全反射后从下端面射向被测物体,经被测物体表面镜面反射至N下端面,N下端面被照亮的面积与玻璃丝下端面到被测物体距离有关。
(1)从M下端面出射的光与竖直方向的最大偏角为θ,求θ的正弦值;
(2)被测物体自上而下微小移动,使N下端面从刚能接收反射激光到恰好全部被照亮,求玻璃丝下端面到被测物体距离b的相应范围(只考虑在被测物体表面反射一次的光线)。
15.(2023·全国卷)如图,一折射率为的棱镜的横截面为等腰直角三角形△ABC,AB=AC=l,BC边所在底面上镀有一层反射膜。一细光束沿垂直于BC方向经AB边上的M点射入棱镜,若这束光被BC边反射后恰好射向顶点A,求M点到A点的距离。
16.(2022·全国甲卷,34(2))如图,边长为a的正方形ABCD为一棱镜的横截面,M为AB边的中点。在截面所在平面内,一光线自M点射入棱镜,入射角为60°,经折射后在BC边的N点恰好发生全反射,反射光线从CD边的P点射出棱镜。求棱镜的折射率以及P、C两点之间的距离。
17.(2021·山东卷,15)超强超短光脉冲产生方法曾获诺贝尔物理学奖,其中用到的一种脉冲激光展宽器截面如图所示。在空气中对称放置四个相同的直角三棱镜,顶角为θ。一细束脉冲激光垂直第一个棱镜左侧面入射,经过前两个棱镜后分为平行的光束,再经过后两个棱镜重新合成为一束,此时不同频率的光前后分开,完成脉冲展宽。已知相邻两棱镜斜面间的距离d=100.0 mm,脉冲激光中包含两种频率的光,它们在棱镜中的折射率分别为n1=和n2=。取sin 37°=,cos 37°=,=1.890。
(1)为使两种频率的光都能从左侧第一个棱镜斜面射出,求θ的取值范围;
(2)若θ=37°,求两种频率的光通过整个展宽器的过程中,在空气中的路程差ΔL(保留3位有效数字)。
第4章 光
一、高考真题探析
典 题 (2022·全国乙卷,34(2))一细束单色光在三棱镜ABC的侧面AC上以大角度由D点入射(入射面在棱镜的横截面内),入射角为i,经折射后射至AB边的E点,如图所示。逐渐减小i,E点向B点移动,当sin i=时,恰好没有光线从AB边射出棱镜,且DE=DA。求棱镜的折射率。
答案:1.5
解析:如图所示,当折射光线在AB边恰好不能射出时,在AB边上的入射角等于全反射临界角C0,
DA=DE,各个角度如图中所示
由几何关系可知
α=90°-C0,
90°-r+2α=180°,
解得r=90°-2C0,
由全反射知识得sin C0=,
由折射定律有n=,
代入sin i=解得n=1.5。
二、临场真题练兵
1.(2023·重庆卷)某实验小组利用双缝干涉实验装置分别观察a、b两单色光的干涉条纹,发现在相同的条件下光屏上a光相邻两亮条纹的间距比b光的小。他们又将a、b光以相同的入射角由水斜射入空气,发现a光的折射角比b光的大,则( D )
A.在空气中传播时,a光的波长比b光的大
B.在水中传播时,a光的速度比b光的大
C.在水中传播时,a光的频率比b光的小
D.由水射向空气时,a光的全反射临界角比b光的小
解析:根据相邻两条亮条纹的间距计算公式Δx=λ,由此可知λa<λb,故A错误;根据折射定律n=,a、b光以相同的入射角由水斜射入空气,a光的折射角比b光的大,则na>nb,根据光在介质中的传播速度与折射率的关系n=,可得在水中传播时,a光的速度比b光的小,故B错误;在水中传播时,a光的折射率比b光的大,所以a光的频率比b光的大,故C错误;根据临界角与折射率的关系n=,可得在水中传播时,a光的折射率比b光的大,a光的全反射临界角比b光的小,故D正确。
2.(2023·山东卷)如图所示为一种干涉热膨胀仪原理图。G为标准石英环,C为待测柱形样品,C的上表面与上方标准平面石英板之间存在劈形空气层。用单色平行光垂直照射上方石英板,会形成干涉条纹。已知C的膨胀系数小于G的膨胀系数,当温度升高时,下列说法正确的是( A )
A.劈形空气层的厚度变大,条纹向左移动
B.劈形空气层的厚度变小,条纹向左移动
C.劈形空气层的厚度变大,条纹向右移动
D.劈形空气层的厚度变小,条纹向右移动
解析:由题知,C的膨胀系数小于G的膨胀系数,当温度升高时,G增长的高度大于C增长的高度,则劈形空气层的厚度变大,且同一厚度的空气膜向劈尖移动,则条纹向左移动。
3.(2023·浙江卷)在水池底部水平放置三条细灯带构成的等腰直角三角形发光体,直角边的长度为0.9 m,水的折射率n=,细灯带到水面的距离h= m,则有光射出的水面形状(用阴影表示)为( C )
A B
C D
解析:灯带发出的光从水面射出时发生全反射临界角的正弦值sin C==,则tan C=,灯带上的一个点发出的光发生全反射的临界角如图所示
根据几何关系可得r=htan C=× m=0.3 m,
则一个点发出的光在水面上能看到的r=0.3 m的圆,光射出的水面形状边缘为弧形,如图所示:
等腰直角三角形发光体的内切圆半径r′满足r′=,解得r′=<=r,故中间无空缺。
4.(2023·湖北卷)如图所示,楔形玻璃的横截面POQ的顶角为30°,OP边上的点光源S到顶点O的距离为d,垂直于OP边的光线SN在OQ边的折射角为45°。不考虑多次反射,OQ边上有光射出部分的长度为( C )
A.d B.d
C.d D.d
解析:设光线在OQ界面的入射角为α,折射角为β,几何关系可知α=30°,则有折射定律n==,光线射出OQ界面的临界为发生全反射,光路图如下,其中OB⊥CS,光线在AB两点发生全反射,有全反射定律sin C==,即AB两处全反射的临界角为45°,AB之间有光线射出,由几何关系可知AB=2AC=2CS=OS=d。
5.(多选)(2023·湖南卷)一位潜水爱好者在水下活动时,利用激光器向岸上救援人员发射激光信号,设激光光束与水面的夹角为α,如图所示。他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,下列说法正确的是( BC )
A.水的折射率为
B.水的折射率为
C.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角小于60°
D.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角大于60°
解析:他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,则说明α=41°时激光恰好发生全反射,则sin (90°-41°)=,则n=,A错误,B正确;当他以α=60°向水面发射激光时,入射角i1=30°,则根据折射定律有nsin i1=sin i2,折射角i2大于30°,则岸上救援人员接收激光光束的方向与水面夹角小于60°,C正确,D错误。
6.(多选)(2023·全国卷)等腰三角形△abc为一棱镜的横截面,ab=ac;一平行于bc边的细光束从ab边射入棱镜,在bc边反射后从ac边射出,出射光分成了不同颜色的两束,甲光的出射点在乙光的下方,如图所示。不考虑多次反射。下列说法正确的是( AC )
A.甲光的波长比乙光的长
B.甲光的频率比乙光的高
C.在棱镜中的传播速度,甲光比乙光的大
D.该棱镜对甲光的折射率大于对乙光的折射率
解析:根据折射定律和反射定律作出光路图如图所示:由图可知,乙光的折射角较小,根据折射定律可知乙光的折射率大,则乙光的频率大,根据c=fλ可知,乙光的波长短,A正确,B、D错误;根据v=可知在棱镜中的传播速度,甲光比乙光的大,C正确。
7.(2022·山东卷,7)柱状光学器件横截面如图所示,OP右侧是以O为圆心、半径为R的圆,左侧是直角梯形,AP长为R,AC与CO夹角为45°,AC中点为B。a、b两种频率的细激光束,垂直AB面入射,器件介质对a、b光的折射率分别为1.42、1.40。保持光的入射方向不变,入射点从A向B移动过程中,能在PM面全反射后,从OM面出射的光是(不考虑三次反射以后的光)( A )
A.仅有a光
B.仅有b光
C.a、b光都可以
D.a、b光都不可以
解析:根据临界角sin C=可知Ca<45°,Cb>45°,从B点入射的光经OC面反射到P点,如图此时的入射角等于45°,则A、B之间入射到PM面上的入射角都小于45°,只有a光能发生全反射,故选项A正确。
8.(2022·辽宁卷,5)完全失重时,液滴呈球形,气泡在液体中将不会上浮。2021年12月,在中国空间站“天宫课堂”的水球光学实验中,航天员向水球中注入空气形成了一个内含气泡的水球。如图所示,若气泡与水球同心,在过球心O的平面内,用单色平行光照射这一水球,下列说法正确的是( C )
A.此单色光从空气进入水球,频率一定变大
B.此单色光从空气进入水球,频率一定变小
C.若光线1在M处发生全反射,光线2在N处一定发生全反射
D.若光线2在N处发生全反射,光线1在M处一定发生全反射
解析:光的频率与介质无关,光从空气进入水球,频率不发生改变,A、B错误;由题图知,光线1在M处的入射角小于光线2在N处的入射角,若光线1在M处发生全反射,说明光线1在M处的入射角已大于或等于发生全反射的临界角,则光线2在N处一定发生全反射,C正确;若光线2在N处发生全反射,光线1在M处的入射角不一定大于或等于发生全反射的临界角,不一定发生全反射,D错误。
9.(2021·山东等级考,7)用平行单色光垂直照射一层透明薄膜,观察到如图所示明暗相间的干涉条纹。下列关于该区域薄膜厚度d随坐标x的变化图像,可能正确的是( D )
解析:从薄膜的上下表面分别反射的两列光是相干光,其光程差为Δx=2d,即光程差为薄膜厚度的2倍,当光程差Δx=nλ时此处出现亮条纹,故相邻亮条纹之间的薄膜的厚度差为λ,在题图中相邻亮条纹(或暗条纹)之间的距离变大,则薄膜层的厚度沿x轴变化的越来越慢,图像斜率越来越小,故D正确,A、B、C错误。
10.(2023·广东卷)某同学用激光笔和透明长方体玻璃砖测量玻璃的折射率,实验过程如下:
(1)将玻璃砖平放在水平桌面上的白纸上,用大头针在白纸上标记玻璃砖的边界
(2)①激光笔发出的激光从玻璃砖上的M点水平入射,到达ef面上的O点后反射到N点射出。用大头针在白纸上标记O点、M点和激光笔出光孔Q的位置
②移走玻璃砖,在白纸上描绘玻璃砖的边界和激光的光路,作QM连线的延长线与ef面的边界交于P点,如图(a)所示
③用刻度尺测量PM和OM的长度d1和d2。PM的示数如图(b)所示,d1为_2.25_cm__。测得d2为3.40 cm。
(3)利用所测量的物理量,写出玻璃砖折射率的表达式n= ;由测得的数据可得折射率n为_1.51__(结果保留3位有效数字)
(4)相对误差的计算式为δ=×100%。为了减小d1、d2测量的相对误差,实验中激光在M点入射时应尽量使入射角_稍小一些__。
解析:(2)刻度尺的最小分度为0.1 cm,由图可知,d1为2.25 cm。
(3)玻璃砖折射率的表达式n====
带入数据可知n==1.51。
(4)相对误差的计算式为δ=×100%,为了减小d1、d2测量的相对误差,实验中d1、d2要尽量稍大一些,即激光在M点入射时应尽量使入射角稍小一些。
11.(2023·海南卷)用激光测玻璃砖折射率的实验中,玻璃砖与屏P平行放置,从另一侧用激光笔以一定角度照射,此时在屏上的S1处有激光点,移走玻璃砖,光点移到S2处,回答下列问题:
(1)请画出激光束经玻璃折射后完整的光路图_见解析__;
(2)已经测出AB=l1,OA=l2,S1S2=l3,则折射率n= (用l1、l2、l3表示);
(3)若改用宽ab更小的玻璃砖做实验,则S1S2间的距离会_变小__(选填“变大”“变小”或“不变”)。
解析:(1)根据题意画出光路图如下图所示
(2)设光线入射角为θ、折射角为α,则在C点根据折射定律有nsin θ=sin α
由于射入玻璃砖的入射角是射出玻璃砖的折射角,则S1S2=CB,根据几何关系可知sin θ=,sin α=,联立解得n=。
(3)若改用宽ab更小的玻璃砖做实验,则画出光路图如下
可看出S1S2间的距离变小。
12.(2021·全国甲卷,34(1))如图,单色光从折射率n=1.5、厚度d=10.0 cm的玻璃板上表面射入。已知真空中的光速为3.0×108 m/s,则该单色光在玻璃板内传播的速度为_2×108__m/s;对于所有可能的入射角,该单色光通过玻璃板所用时间t的取值范围是_5×10-10__s≤t< 3×10-10 s (不考虑反射)。
解析:该单色光在玻璃板内传播的速度为
v== m/s=2×108 m/s,
当光垂直玻璃板射入时,光不发生偏折,该单色光通过玻璃板所用时间最短,最短时间
t1== s=5×10-10 s,
当光的入射角是90°时,该单色光通过玻璃板所用时间最长。由折射定律可知
n=,
最长时间
t2===3×10-10 s。
13.(2021·浙江6月选考,17(2))如图所示是“用双缝干涉测量光的波长”实验的装置。实验中:
(1)观察到较模糊的干涉条纹,要使条纹变得清晰,值得尝试的是_C__(单选)。
A.旋转测量头
B.增大单缝与双缝间的距离
C.调节拨杆使单缝与双缝平行
(2)要增大观察到的条纹间距,正确的做法是_D__(单选)。
A.减小单缝与光源间的距离
B.减小单缝与双缝间的距离
C.增大透镜与单缝间的距离
D.增大双缝与测量头间的距离
解析:(1)旋转测量头只能调节分划板的刻度线与干涉条纹是否平行,不能调节清晰程度,选项A错误;增大单缝与双缝之间的距离既不能调节干涉条纹间隔,也不能调节清晰程度,选项B错误;调节拨杆使单缝与双缝平行,使得经过单缝后形成的中心最宽的衍射条纹经过双缝更容易发生清晰的双缝干涉现象,选项C正确。
(2)根据双缝干涉条纹间隔公式Δx=可知,增加双缝到屏幕(测量头)的距离L、光的波长λ,减小双缝宽度d都可以增加条纹间距,由此可知选项D正确;增加或减小单缝与双缝间的距离、单缝与光源间的距离,并不能观察到条纹间距的变化,选项A、B错误;增加透镜与单缝间的距离也不能改变观察到的条纹间距,选项C错误。
14.(2023·山东卷)一种反射式光纤位移传感器可以实现微小位移测量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝M、N,相距为d,直径均为2a,折射率为n(n<)。M、N下端横截面平齐且与被测物体表面平行。激光在M内多次全反射后从下端面射向被测物体,经被测物体表面镜面反射至N下端面,N下端面被照亮的面积与玻璃丝下端面到被测物体距离有关。
(1)从M下端面出射的光与竖直方向的最大偏角为θ,求θ的正弦值;
(2)被测物体自上而下微小移动,使N下端面从刚能接收反射激光到恰好全部被照亮,求玻璃丝下端面到被测物体距离b的相应范围(只考虑在被测物体表面反射一次的光线)。
答案:(1)sin θ= (2)解析:(1)由题意可知当光在两侧刚好发生全反射时从M下端面出射的光与竖直方向夹角最大,设光在M下端入射角为α,此时sin C==cos α
可得sin α=
又因为n=
所以sin θ=nsin α=。
(2)根据题意要使N下端面从刚能接收反射激光到恰好全部被照亮,光路图如图所示
则玻璃丝下端面到被测物体距离b的相应范围应该为b1当距离最近时有tan θ=
当距离最远时有tan θ=
根据(1)可知tan θ=
联立可得b1=,b2=
所以满足条件的范围为15.(2023·全国卷)如图,一折射率为的棱镜的横截面为等腰直角三角形△ABC,AB=AC=l,BC边所在底面上镀有一层反射膜。一细光束沿垂直于BC方向经AB边上的M点射入棱镜,若这束光被BC边反射后恰好射向顶点A,求M点到A点的距离。
答案:l
解析:由题意可知做出光路图如图所示:
光线垂直于BC方向射入,根据几何关系可知入射角为45°;由于棱镜折射率为,根据n=
有sin r=
则折射角为30°;∠BMO=60°,因为∠B=45°,所以光在BC面的入射角为θ=90°-(180°-60°-45°)=15°
根据反射定律可知∠MOA=2θ=30°
根据几何关系可知∠BAO=30°,即△MAO为等腰三角形,则=
又因为△BOM与△CAO相似,故有=
由题知AB=AC=l
联立可得BM=AC=l
所以M到A点的距离为x=MA=l-BM=l。
16.(2022·全国甲卷,34(2))如图,边长为a的正方形ABCD为一棱镜的横截面,M为AB边的中点。在截面所在平面内,一光线自M点射入棱镜,入射角为60°,经折射后在BC边的N点恰好发生全反射,反射光线从CD边的P点射出棱镜。求棱镜的折射率以及P、C两点之间的距离。
答案: a
解析:设光在AB面的折射角为r,则由折射定律有n=,
光在BC面恰发生全反射,有sin C=,
由几何知识有r+C=90°,
联立解得tan r=,n=,
据几何关系有tan r==,
又MB=,BN+NC=a
联立解得PC=a。
17.(2021·山东卷,15)超强超短光脉冲产生方法曾获诺贝尔物理学奖,其中用到的一种脉冲激光展宽器截面如图所示。在空气中对称放置四个相同的直角三棱镜,顶角为θ。一细束脉冲激光垂直第一个棱镜左侧面入射,经过前两个棱镜后分为平行的光束,再经过后两个棱镜重新合成为一束,此时不同频率的光前后分开,完成脉冲展宽。已知相邻两棱镜斜面间的距离d=100.0 mm,脉冲激光中包含两种频率的光,它们在棱镜中的折射率分别为n1=和n2=。取sin 37°=,cos 37°=,=1.890。
(1)为使两种频率的光都能从左侧第一个棱镜斜面射出,求θ的取值范围;
(2)若θ=37°,求两种频率的光通过整个展宽器的过程中,在空气中的路程差ΔL(保留3位有效数字)。
答案:(1)0<θ<45°(或θ<45°) (2)ΔL=14.4 mm
解析:(1)设C是全反射的临界角,光线在第一个三棱镜右侧斜面上恰好发生全反射时,根据折射定律得sin C=
代入较大的折射率得C=45°
所以顶角θ的范围为0<θ<45°(或θ<45°)。
(2)脉冲激光从第一个三棱镜右侧斜面射出时发生折射,设折射角分别为α1和α2,由折射定律得
n1= ①,n2= ②
设两束光在前两个三棱镜斜面之间的路程分别为L1和L2,则
L1=③ L2=④
ΔL=2(L1-L2)⑤
联立①②③④⑤式,代入数据得ΔL=14.4 mm。
一、高考真题探析
典 题 (2022·全国乙卷,34(2))一细束单色光在三棱镜ABC的侧面AC上以大角度由D点入射(入射面在棱镜的横截面内),入射角为i,经折射后射至AB边的E点,如图所示。逐渐减小i,E点向B点移动,当sin i=时,恰好没有光线从AB边射出棱镜,且DE=DA。求棱镜的折射率。
二、临场真题练兵
1.(2023·重庆卷)某实验小组利用双缝干涉实验装置分别观察a、b两单色光的干涉条纹,发现在相同的条件下光屏上a光相邻两亮条纹的间距比b光的小。他们又将a、b光以相同的入射角由水斜射入空气,发现a光的折射角比b光的大,则( D )
A.在空气中传播时,a光的波长比b光的大
B.在水中传播时,a光的速度比b光的大
C.在水中传播时,a光的频率比b光的小
D.由水射向空气时,a光的全反射临界角比b光的小
2.(2023·山东卷)如图所示为一种干涉热膨胀仪原理图。G为标准石英环,C为待测柱形样品,C的上表面与上方标准平面石英板之间存在劈形空气层。用单色平行光垂直照射上方石英板,会形成干涉条纹。已知C的膨胀系数小于G的膨胀系数,当温度升高时,下列说法正确的是( A )
A.劈形空气层的厚度变大,条纹向左移动
B.劈形空气层的厚度变小,条纹向左移动
C.劈形空气层的厚度变大,条纹向右移动
D.劈形空气层的厚度变小,条纹向右移动
3.(2023·浙江卷)在水池底部水平放置三条细灯带构成的等腰直角三角形发光体,直角边的长度为0.9 m,水的折射率n=,细灯带到水面的距离h= m,则有光射出的水面形状(用阴影表示)为( C )
A B
C D
4.(2023·湖北卷)如图所示,楔形玻璃的横截面POQ的顶角为30°,OP边上的点光源S到顶点O的距离为d,垂直于OP边的光线SN在OQ边的折射角为45°。不考虑多次反射,OQ边上有光射出部分的长度为( C )
A.d B.d
C.d D.d
5.(多选)(2023·湖南卷)一位潜水爱好者在水下活动时,利用激光器向岸上救援人员发射激光信号,设激光光束与水面的夹角为α,如图所示。他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,下列说法正确的是( BC )
A.水的折射率为
B.水的折射率为
C.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角小于60°
D.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角大于60°
6.(多选)(2023·全国卷)等腰三角形△abc为一棱镜的横截面,ab=ac;一平行于bc边的细光束从ab边射入棱镜,在bc边反射后从ac边射出,出射光分成了不同颜色的两束,甲光的出射点在乙光的下方,如图所示。不考虑多次反射。下列说法正确的是( AC )
A.甲光的波长比乙光的长
B.甲光的频率比乙光的高
C.在棱镜中的传播速度,甲光比乙光的大
D.该棱镜对甲光的折射率大于对乙光的折射率
7.(2022·山东卷,7)柱状光学器件横截面如图所示,OP右侧是以O为圆心、半径为R的圆,左侧是直角梯形,AP长为R,AC与CO夹角为45°,AC中点为B。a、b两种频率的细激光束,垂直AB面入射,器件介质对a、b光的折射率分别为1.42、1.40。保持光的入射方向不变,入射点从A向B移动过程中,能在PM面全反射后,从OM面出射的光是(不考虑三次反射以后的光)( A )
A.仅有a光
B.仅有b光
C.a、b光都可以
D.a、b光都不可以
8.(2022·辽宁卷,5)完全失重时,液滴呈球形,气泡在液体中将不会上浮。2021年12月,在中国空间站“天宫课堂”的水球光学实验中,航天员向水球中注入空气形成了一个内含气泡的水球。如图所示,若气泡与水球同心,在过球心O的平面内,用单色平行光照射这一水球,下列说法正确的是( C )
A.此单色光从空气进入水球,频率一定变大
B.此单色光从空气进入水球,频率一定变小
C.若光线1在M处发生全反射,光线2在N处一定发生全反射
D.若光线2在N处发生全反射,光线1在M处一定发生全反射
9.(2021·山东等级考,7)用平行单色光垂直照射一层透明薄膜,观察到如图所示明暗相间的干涉条纹。下列关于该区域薄膜厚度d随坐标x的变化图像,可能正确的是( D )
10.(2023·广东卷)某同学用激光笔和透明长方体玻璃砖测量玻璃的折射率,实验过程如下:
(1)将玻璃砖平放在水平桌面上的白纸上,用大头针在白纸上标记玻璃砖的边界
(2)①激光笔发出的激光从玻璃砖上的M点水平入射,到达ef面上的O点后反射到N点射出。用大头针在白纸上标记O点、M点和激光笔出光孔Q的位置
②移走玻璃砖,在白纸上描绘玻璃砖的边界和激光的光路,作QM连线的延长线与ef面的边界交于P点,如图(a)所示
③用刻度尺测量PM和OM的长度d1和d2。PM的示数如图(b)所示,d1为___。测得d2为3.40 cm。
(3)利用所测量的物理量,写出玻璃砖折射率的表达式n= ;由测得的数据可得折射率n为___(结果保留3位有效数字)
(4)相对误差的计算式为δ=×100%。为了减小d1、d2测量的相对误差,实验中激光在M点入射时应尽量使入射角___。
11.(2023·海南卷)用激光测玻璃砖折射率的实验中,玻璃砖与屏P平行放置,从另一侧用激光笔以一定角度照射,此时在屏上的S1处有激光点,移走玻璃砖,光点移到S2处,回答下列问题:
(1)请画出激光束经玻璃折射后完整的光路图___;
(2)已经测出AB=l1,OA=l2,S1S2=l3,则折射率n= (用l1、l2、l3表示);
(3)若改用宽ab更小的玻璃砖做实验,则S1S2间的距离会___(选填“变大”“变小”或“不变”)。
12.(2021·全国甲卷,34(1))如图,单色光从折射率n=1.5、厚度d=10.0 cm的玻璃板上表面射入。已知真空中的光速为3.0×108 m/s,则该单色光在玻璃板内传播的速度为___m/s;对于所有可能的入射角,该单色光通过玻璃板所用时间t的取值范围是___s≤t< s (不考虑反射)。
13.(2021·浙江6月选考,17(2))如图所示是“用双缝干涉测量光的波长”实验的装置。实验中:
(1)观察到较模糊的干涉条纹,要使条纹变得清晰,值得尝试的是___(单选)。
A.旋转测量头
B.增大单缝与双缝间的距离
C.调节拨杆使单缝与双缝平行
(2)要增大观察到的条纹间距,正确的做法是___(单选)。
A.减小单缝与光源间的距离
B.减小单缝与双缝间的距离
C.增大透镜与单缝间的距离
D.增大双缝与测量头间的距离
14.(2023·山东卷)一种反射式光纤位移传感器可以实现微小位移测量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝M、N,相距为d,直径均为2a,折射率为n(n<)。M、N下端横截面平齐且与被测物体表面平行。激光在M内多次全反射后从下端面射向被测物体,经被测物体表面镜面反射至N下端面,N下端面被照亮的面积与玻璃丝下端面到被测物体距离有关。
(1)从M下端面出射的光与竖直方向的最大偏角为θ,求θ的正弦值;
(2)被测物体自上而下微小移动,使N下端面从刚能接收反射激光到恰好全部被照亮,求玻璃丝下端面到被测物体距离b的相应范围(只考虑在被测物体表面反射一次的光线)。
15.(2023·全国卷)如图,一折射率为的棱镜的横截面为等腰直角三角形△ABC,AB=AC=l,BC边所在底面上镀有一层反射膜。一细光束沿垂直于BC方向经AB边上的M点射入棱镜,若这束光被BC边反射后恰好射向顶点A,求M点到A点的距离。
16.(2022·全国甲卷,34(2))如图,边长为a的正方形ABCD为一棱镜的横截面,M为AB边的中点。在截面所在平面内,一光线自M点射入棱镜,入射角为60°,经折射后在BC边的N点恰好发生全反射,反射光线从CD边的P点射出棱镜。求棱镜的折射率以及P、C两点之间的距离。
17.(2021·山东卷,15)超强超短光脉冲产生方法曾获诺贝尔物理学奖,其中用到的一种脉冲激光展宽器截面如图所示。在空气中对称放置四个相同的直角三棱镜,顶角为θ。一细束脉冲激光垂直第一个棱镜左侧面入射,经过前两个棱镜后分为平行的光束,再经过后两个棱镜重新合成为一束,此时不同频率的光前后分开,完成脉冲展宽。已知相邻两棱镜斜面间的距离d=100.0 mm,脉冲激光中包含两种频率的光,它们在棱镜中的折射率分别为n1=和n2=。取sin 37°=,cos 37°=,=1.890。
(1)为使两种频率的光都能从左侧第一个棱镜斜面射出,求θ的取值范围;
(2)若θ=37°,求两种频率的光通过整个展宽器的过程中,在空气中的路程差ΔL(保留3位有效数字)。
第4章 光
一、高考真题探析
典 题 (2022·全国乙卷,34(2))一细束单色光在三棱镜ABC的侧面AC上以大角度由D点入射(入射面在棱镜的横截面内),入射角为i,经折射后射至AB边的E点,如图所示。逐渐减小i,E点向B点移动,当sin i=时,恰好没有光线从AB边射出棱镜,且DE=DA。求棱镜的折射率。
答案:1.5
解析:如图所示,当折射光线在AB边恰好不能射出时,在AB边上的入射角等于全反射临界角C0,
DA=DE,各个角度如图中所示
由几何关系可知
α=90°-C0,
90°-r+2α=180°,
解得r=90°-2C0,
由全反射知识得sin C0=,
由折射定律有n=,
代入sin i=解得n=1.5。
二、临场真题练兵
1.(2023·重庆卷)某实验小组利用双缝干涉实验装置分别观察a、b两单色光的干涉条纹,发现在相同的条件下光屏上a光相邻两亮条纹的间距比b光的小。他们又将a、b光以相同的入射角由水斜射入空气,发现a光的折射角比b光的大,则( D )
A.在空气中传播时,a光的波长比b光的大
B.在水中传播时,a光的速度比b光的大
C.在水中传播时,a光的频率比b光的小
D.由水射向空气时,a光的全反射临界角比b光的小
解析:根据相邻两条亮条纹的间距计算公式Δx=λ,由此可知λa<λb,故A错误;根据折射定律n=,a、b光以相同的入射角由水斜射入空气,a光的折射角比b光的大,则na>nb,根据光在介质中的传播速度与折射率的关系n=,可得在水中传播时,a光的速度比b光的小,故B错误;在水中传播时,a光的折射率比b光的大,所以a光的频率比b光的大,故C错误;根据临界角与折射率的关系n=,可得在水中传播时,a光的折射率比b光的大,a光的全反射临界角比b光的小,故D正确。
2.(2023·山东卷)如图所示为一种干涉热膨胀仪原理图。G为标准石英环,C为待测柱形样品,C的上表面与上方标准平面石英板之间存在劈形空气层。用单色平行光垂直照射上方石英板,会形成干涉条纹。已知C的膨胀系数小于G的膨胀系数,当温度升高时,下列说法正确的是( A )
A.劈形空气层的厚度变大,条纹向左移动
B.劈形空气层的厚度变小,条纹向左移动
C.劈形空气层的厚度变大,条纹向右移动
D.劈形空气层的厚度变小,条纹向右移动
解析:由题知,C的膨胀系数小于G的膨胀系数,当温度升高时,G增长的高度大于C增长的高度,则劈形空气层的厚度变大,且同一厚度的空气膜向劈尖移动,则条纹向左移动。
3.(2023·浙江卷)在水池底部水平放置三条细灯带构成的等腰直角三角形发光体,直角边的长度为0.9 m,水的折射率n=,细灯带到水面的距离h= m,则有光射出的水面形状(用阴影表示)为( C )
A B
C D
解析:灯带发出的光从水面射出时发生全反射临界角的正弦值sin C==,则tan C=,灯带上的一个点发出的光发生全反射的临界角如图所示
根据几何关系可得r=htan C=× m=0.3 m,
则一个点发出的光在水面上能看到的r=0.3 m的圆,光射出的水面形状边缘为弧形,如图所示:
等腰直角三角形发光体的内切圆半径r′满足r′=,解得r′=<=r,故中间无空缺。
4.(2023·湖北卷)如图所示,楔形玻璃的横截面POQ的顶角为30°,OP边上的点光源S到顶点O的距离为d,垂直于OP边的光线SN在OQ边的折射角为45°。不考虑多次反射,OQ边上有光射出部分的长度为( C )
A.d B.d
C.d D.d
解析:设光线在OQ界面的入射角为α,折射角为β,几何关系可知α=30°,则有折射定律n==,光线射出OQ界面的临界为发生全反射,光路图如下,其中OB⊥CS,光线在AB两点发生全反射,有全反射定律sin C==,即AB两处全反射的临界角为45°,AB之间有光线射出,由几何关系可知AB=2AC=2CS=OS=d。
5.(多选)(2023·湖南卷)一位潜水爱好者在水下活动时,利用激光器向岸上救援人员发射激光信号,设激光光束与水面的夹角为α,如图所示。他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,下列说法正确的是( BC )
A.水的折射率为
B.水的折射率为
C.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角小于60°
D.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角大于60°
解析:他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,则说明α=41°时激光恰好发生全反射,则sin (90°-41°)=,则n=,A错误,B正确;当他以α=60°向水面发射激光时,入射角i1=30°,则根据折射定律有nsin i1=sin i2,折射角i2大于30°,则岸上救援人员接收激光光束的方向与水面夹角小于60°,C正确,D错误。
6.(多选)(2023·全国卷)等腰三角形△abc为一棱镜的横截面,ab=ac;一平行于bc边的细光束从ab边射入棱镜,在bc边反射后从ac边射出,出射光分成了不同颜色的两束,甲光的出射点在乙光的下方,如图所示。不考虑多次反射。下列说法正确的是( AC )
A.甲光的波长比乙光的长
B.甲光的频率比乙光的高
C.在棱镜中的传播速度,甲光比乙光的大
D.该棱镜对甲光的折射率大于对乙光的折射率
解析:根据折射定律和反射定律作出光路图如图所示:由图可知,乙光的折射角较小,根据折射定律可知乙光的折射率大,则乙光的频率大,根据c=fλ可知,乙光的波长短,A正确,B、D错误;根据v=可知在棱镜中的传播速度,甲光比乙光的大,C正确。
7.(2022·山东卷,7)柱状光学器件横截面如图所示,OP右侧是以O为圆心、半径为R的圆,左侧是直角梯形,AP长为R,AC与CO夹角为45°,AC中点为B。a、b两种频率的细激光束,垂直AB面入射,器件介质对a、b光的折射率分别为1.42、1.40。保持光的入射方向不变,入射点从A向B移动过程中,能在PM面全反射后,从OM面出射的光是(不考虑三次反射以后的光)( A )
A.仅有a光
B.仅有b光
C.a、b光都可以
D.a、b光都不可以
解析:根据临界角sin C=可知Ca<45°,Cb>45°,从B点入射的光经OC面反射到P点,如图此时的入射角等于45°,则A、B之间入射到PM面上的入射角都小于45°,只有a光能发生全反射,故选项A正确。
8.(2022·辽宁卷,5)完全失重时,液滴呈球形,气泡在液体中将不会上浮。2021年12月,在中国空间站“天宫课堂”的水球光学实验中,航天员向水球中注入空气形成了一个内含气泡的水球。如图所示,若气泡与水球同心,在过球心O的平面内,用单色平行光照射这一水球,下列说法正确的是( C )
A.此单色光从空气进入水球,频率一定变大
B.此单色光从空气进入水球,频率一定变小
C.若光线1在M处发生全反射,光线2在N处一定发生全反射
D.若光线2在N处发生全反射,光线1在M处一定发生全反射
解析:光的频率与介质无关,光从空气进入水球,频率不发生改变,A、B错误;由题图知,光线1在M处的入射角小于光线2在N处的入射角,若光线1在M处发生全反射,说明光线1在M处的入射角已大于或等于发生全反射的临界角,则光线2在N处一定发生全反射,C正确;若光线2在N处发生全反射,光线1在M处的入射角不一定大于或等于发生全反射的临界角,不一定发生全反射,D错误。
9.(2021·山东等级考,7)用平行单色光垂直照射一层透明薄膜,观察到如图所示明暗相间的干涉条纹。下列关于该区域薄膜厚度d随坐标x的变化图像,可能正确的是( D )
解析:从薄膜的上下表面分别反射的两列光是相干光,其光程差为Δx=2d,即光程差为薄膜厚度的2倍,当光程差Δx=nλ时此处出现亮条纹,故相邻亮条纹之间的薄膜的厚度差为λ,在题图中相邻亮条纹(或暗条纹)之间的距离变大,则薄膜层的厚度沿x轴变化的越来越慢,图像斜率越来越小,故D正确,A、B、C错误。
10.(2023·广东卷)某同学用激光笔和透明长方体玻璃砖测量玻璃的折射率,实验过程如下:
(1)将玻璃砖平放在水平桌面上的白纸上,用大头针在白纸上标记玻璃砖的边界
(2)①激光笔发出的激光从玻璃砖上的M点水平入射,到达ef面上的O点后反射到N点射出。用大头针在白纸上标记O点、M点和激光笔出光孔Q的位置
②移走玻璃砖,在白纸上描绘玻璃砖的边界和激光的光路,作QM连线的延长线与ef面的边界交于P点,如图(a)所示
③用刻度尺测量PM和OM的长度d1和d2。PM的示数如图(b)所示,d1为_2.25_cm__。测得d2为3.40 cm。
(3)利用所测量的物理量,写出玻璃砖折射率的表达式n= ;由测得的数据可得折射率n为_1.51__(结果保留3位有效数字)
(4)相对误差的计算式为δ=×100%。为了减小d1、d2测量的相对误差,实验中激光在M点入射时应尽量使入射角_稍小一些__。
解析:(2)刻度尺的最小分度为0.1 cm,由图可知,d1为2.25 cm。
(3)玻璃砖折射率的表达式n====
带入数据可知n==1.51。
(4)相对误差的计算式为δ=×100%,为了减小d1、d2测量的相对误差,实验中d1、d2要尽量稍大一些,即激光在M点入射时应尽量使入射角稍小一些。
11.(2023·海南卷)用激光测玻璃砖折射率的实验中,玻璃砖与屏P平行放置,从另一侧用激光笔以一定角度照射,此时在屏上的S1处有激光点,移走玻璃砖,光点移到S2处,回答下列问题:
(1)请画出激光束经玻璃折射后完整的光路图_见解析__;
(2)已经测出AB=l1,OA=l2,S1S2=l3,则折射率n= (用l1、l2、l3表示);
(3)若改用宽ab更小的玻璃砖做实验,则S1S2间的距离会_变小__(选填“变大”“变小”或“不变”)。
解析:(1)根据题意画出光路图如下图所示
(2)设光线入射角为θ、折射角为α,则在C点根据折射定律有nsin θ=sin α
由于射入玻璃砖的入射角是射出玻璃砖的折射角,则S1S2=CB,根据几何关系可知sin θ=,sin α=,联立解得n=。
(3)若改用宽ab更小的玻璃砖做实验,则画出光路图如下
可看出S1S2间的距离变小。
12.(2021·全国甲卷,34(1))如图,单色光从折射率n=1.5、厚度d=10.0 cm的玻璃板上表面射入。已知真空中的光速为3.0×108 m/s,则该单色光在玻璃板内传播的速度为_2×108__m/s;对于所有可能的入射角,该单色光通过玻璃板所用时间t的取值范围是_5×10-10__s≤t< 3×10-10 s (不考虑反射)。
解析:该单色光在玻璃板内传播的速度为
v== m/s=2×108 m/s,
当光垂直玻璃板射入时,光不发生偏折,该单色光通过玻璃板所用时间最短,最短时间
t1== s=5×10-10 s,
当光的入射角是90°时,该单色光通过玻璃板所用时间最长。由折射定律可知
n=,
最长时间
t2===3×10-10 s。
13.(2021·浙江6月选考,17(2))如图所示是“用双缝干涉测量光的波长”实验的装置。实验中:
(1)观察到较模糊的干涉条纹,要使条纹变得清晰,值得尝试的是_C__(单选)。
A.旋转测量头
B.增大单缝与双缝间的距离
C.调节拨杆使单缝与双缝平行
(2)要增大观察到的条纹间距,正确的做法是_D__(单选)。
A.减小单缝与光源间的距离
B.减小单缝与双缝间的距离
C.增大透镜与单缝间的距离
D.增大双缝与测量头间的距离
解析:(1)旋转测量头只能调节分划板的刻度线与干涉条纹是否平行,不能调节清晰程度,选项A错误;增大单缝与双缝之间的距离既不能调节干涉条纹间隔,也不能调节清晰程度,选项B错误;调节拨杆使单缝与双缝平行,使得经过单缝后形成的中心最宽的衍射条纹经过双缝更容易发生清晰的双缝干涉现象,选项C正确。
(2)根据双缝干涉条纹间隔公式Δx=可知,增加双缝到屏幕(测量头)的距离L、光的波长λ,减小双缝宽度d都可以增加条纹间距,由此可知选项D正确;增加或减小单缝与双缝间的距离、单缝与光源间的距离,并不能观察到条纹间距的变化,选项A、B错误;增加透镜与单缝间的距离也不能改变观察到的条纹间距,选项C错误。
14.(2023·山东卷)一种反射式光纤位移传感器可以实现微小位移测量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝M、N,相距为d,直径均为2a,折射率为n(n<)。M、N下端横截面平齐且与被测物体表面平行。激光在M内多次全反射后从下端面射向被测物体,经被测物体表面镜面反射至N下端面,N下端面被照亮的面积与玻璃丝下端面到被测物体距离有关。
(1)从M下端面出射的光与竖直方向的最大偏角为θ,求θ的正弦值;
(2)被测物体自上而下微小移动,使N下端面从刚能接收反射激光到恰好全部被照亮,求玻璃丝下端面到被测物体距离b的相应范围(只考虑在被测物体表面反射一次的光线)。
答案:(1)sin θ= (2)
可得sin α=
又因为n=
所以sin θ=nsin α=。
(2)根据题意要使N下端面从刚能接收反射激光到恰好全部被照亮,光路图如图所示
则玻璃丝下端面到被测物体距离b的相应范围应该为b1
当距离最远时有tan θ=
根据(1)可知tan θ=
联立可得b1=,b2=
所以满足条件的范围为
答案:l
解析:由题意可知做出光路图如图所示:
光线垂直于BC方向射入,根据几何关系可知入射角为45°;由于棱镜折射率为,根据n=
有sin r=
则折射角为30°;∠BMO=60°,因为∠B=45°,所以光在BC面的入射角为θ=90°-(180°-60°-45°)=15°
根据反射定律可知∠MOA=2θ=30°
根据几何关系可知∠BAO=30°,即△MAO为等腰三角形,则=
又因为△BOM与△CAO相似,故有=
由题知AB=AC=l
联立可得BM=AC=l
所以M到A点的距离为x=MA=l-BM=l。
16.(2022·全国甲卷,34(2))如图,边长为a的正方形ABCD为一棱镜的横截面,M为AB边的中点。在截面所在平面内,一光线自M点射入棱镜,入射角为60°,经折射后在BC边的N点恰好发生全反射,反射光线从CD边的P点射出棱镜。求棱镜的折射率以及P、C两点之间的距离。
答案: a
解析:设光在AB面的折射角为r,则由折射定律有n=,
光在BC面恰发生全反射,有sin C=,
由几何知识有r+C=90°,
联立解得tan r=,n=,
据几何关系有tan r==,
又MB=,BN+NC=a
联立解得PC=a。
17.(2021·山东卷,15)超强超短光脉冲产生方法曾获诺贝尔物理学奖,其中用到的一种脉冲激光展宽器截面如图所示。在空气中对称放置四个相同的直角三棱镜,顶角为θ。一细束脉冲激光垂直第一个棱镜左侧面入射,经过前两个棱镜后分为平行的光束,再经过后两个棱镜重新合成为一束,此时不同频率的光前后分开,完成脉冲展宽。已知相邻两棱镜斜面间的距离d=100.0 mm,脉冲激光中包含两种频率的光,它们在棱镜中的折射率分别为n1=和n2=。取sin 37°=,cos 37°=,=1.890。
(1)为使两种频率的光都能从左侧第一个棱镜斜面射出,求θ的取值范围;
(2)若θ=37°,求两种频率的光通过整个展宽器的过程中,在空气中的路程差ΔL(保留3位有效数字)。
答案:(1)0<θ<45°(或θ<45°) (2)ΔL=14.4 mm
解析:(1)设C是全反射的临界角,光线在第一个三棱镜右侧斜面上恰好发生全反射时,根据折射定律得sin C=
代入较大的折射率得C=45°
所以顶角θ的范围为0<θ<45°(或θ<45°)。
(2)脉冲激光从第一个三棱镜右侧斜面射出时发生折射,设折射角分别为α1和α2,由折射定律得
n1= ①,n2= ②
设两束光在前两个三棱镜斜面之间的路程分别为L1和L2,则
L1=③ L2=④
ΔL=2(L1-L2)⑤
联立①②③④⑤式,代入数据得ΔL=14.4 mm。
