新人教版选择性必修第一册 第2章 机械振动真题演练(含答案)
文档属性
| 名称 | 新人教版选择性必修第一册 第2章 机械振动真题演练(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 825.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-05-10 00:00:00 | ||
图片预览


文档简介
第2章 机械振动
一、高考真题探析
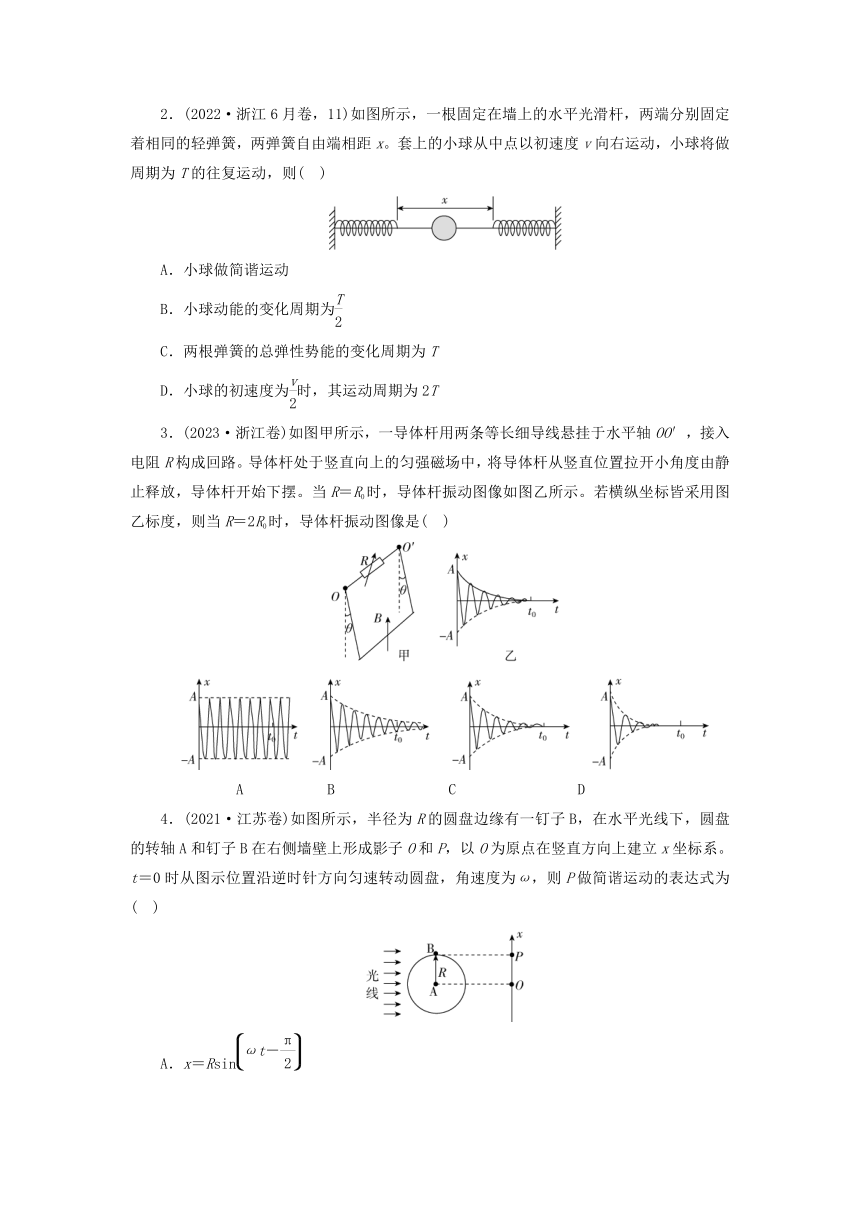
典 题 (2019·全国卷)如图,长为l的细绳下方悬挂一小球a。绳的另一端固定在天花板上O点处,在O点正下方l的O′处有一固定细铁钉。将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时。当小球a摆至最低位置时,细绳会受到铁钉的阻挡。设小球相对于其平衡位置的水平位移为x,向右为正。下列图像中,能描述小球在开始一个周期内的x-t关系的是( )
二、临场真题练兵
1.(2022·湖南卷,16(1))下端附着重物的粗细均匀木棒,竖直浮在河面,在重力和浮力作用下,沿竖直方向做频率为1 Hz的简谐运动;与此同时,木棒在水平方向上随河水做匀速直线运动,如图(a)所示。以木棒所受浮力F为纵轴,木棒水平位移x为横轴建立直角坐标系,浮力F随水平位移x的变化如图(b)所示。已知河水密度为ρ,木棒横截面积为S,重力加速度大小为g。下列说法正确的是( )
A.x从0.05 m到0.15 m的过程中,木棒的动能先增大后减小
B.x从0.21 m到0.25 m的过程中,木棒加速度方向竖直向下,大小逐渐变小
C.x=0.35 m和x=0.45 m时,木棒的速度大小相等,方向相反
D.木棒在竖直方向做简谐运动的振幅为
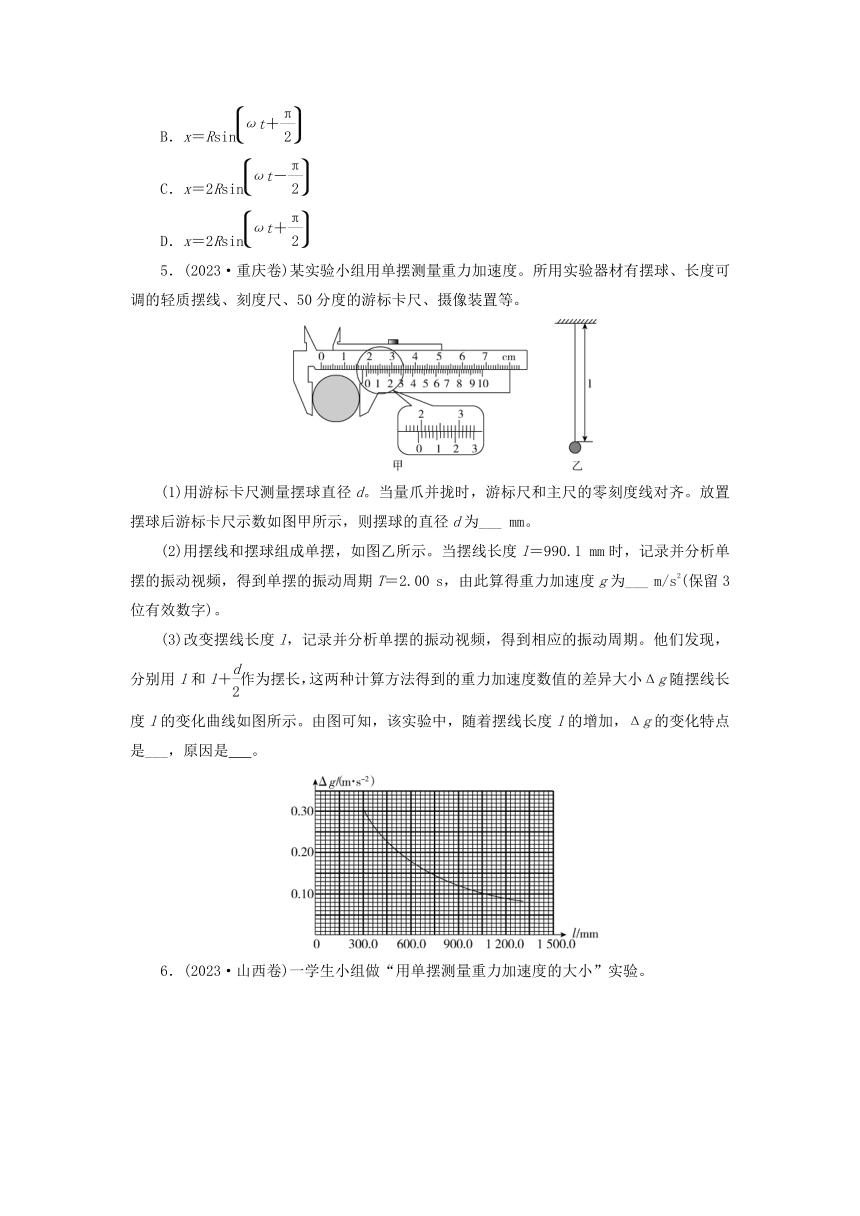
2.(2022·浙江6月卷,11)如图所示,一根固定在墙上的水平光滑杆,两端分别固定着相同的轻弹簧,两弹簧自由端相距x。套上的小球从中点以初速度v向右运动,小球将做周期为T的往复运动,则( )
A.小球做简谐运动
B.小球动能的变化周期为
C.两根弹簧的总弹性势能的变化周期为T
D.小球的初速度为时,其运动周期为2T
3.(2023·浙江卷)如图甲所示,一导体杆用两条等长细导线悬挂于水平轴OO′,接入电阻R构成回路。导体杆处于竖直向上的匀强磁场中,将导体杆从竖直位置拉开小角度由静止释放,导体杆开始下摆。当R=R0时,导体杆振动图像如图乙所示。若横纵坐标皆采用图乙标度,则当R=2R0时,导体杆振动图像是( )
A B C D
4.(2021·江苏卷)如图所示,半径为R的圆盘边缘有一钉子B,在水平光线下,圆盘的转轴A和钉子B在右侧墙壁上形成影子O和P,以O为原点在竖直方向上建立x坐标系。t=0时从图示位置沿逆时针方向匀速转动圆盘,角速度为ω,则P做简谐运动的表达式为( )
A.x=Rsin
B.x=Rsin
C.x=2Rsin
D.x=2Rsin
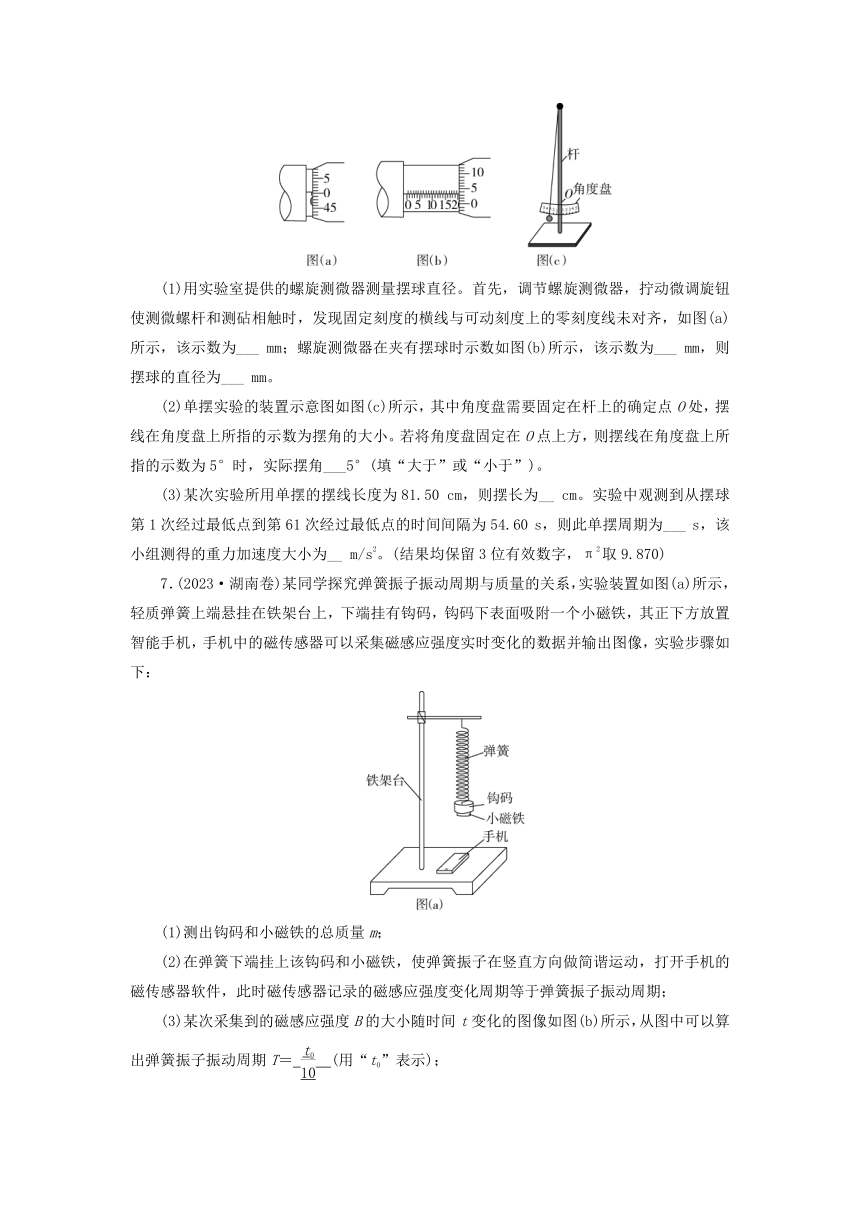
5.(2023·重庆卷)某实验小组用单摆测量重力加速度。所用实验器材有摆球、长度可调的轻质摆线、刻度尺、50分度的游标卡尺、摄像装置等。
(1)用游标卡尺测量摆球直径d。当量爪并拢时,游标尺和主尺的零刻度线对齐。放置摆球后游标卡尺示数如图甲所示,则摆球的直径d为___ mm。
(2)用摆线和摆球组成单摆,如图乙所示。当摆线长度l=990.1 mm时,记录并分析单摆的振动视频,得到单摆的振动周期T=2.00 s,由此算得重力加速度g为___ m/s2(保留3位有效数字)。
(3)改变摆线长度l,记录并分析单摆的振动视频,得到相应的振动周期。他们发现,分别用l和l+作为摆长,这两种计算方法得到的重力加速度数值的差异大小Δg随摆线长度l的变化曲线如图所示。由图可知,该实验中,随着摆线长度l的增加,Δg的变化特点是___,原因是 。
6.(2023·山西卷)一学生小组做“用单摆测量重力加速度的大小”实验。
(1)用实验室提供的螺旋测微器测量摆球直径。首先,调节螺旋测微器,拧动微调旋钮使测微螺杆和测砧相触时,发现固定刻度的横线与可动刻度上的零刻度线未对齐,如图(a)所示,该示数为___ mm;螺旋测微器在夹有摆球时示数如图(b)所示,该示数为___ mm,则摆球的直径为___ mm。
(2)单摆实验的装置示意图如图(c)所示,其中角度盘需要固定在杆上的确定点O处,摆线在角度盘上所指的示数为摆角的大小。若将角度盘固定在O点上方,则摆线在角度盘上所指的示数为5°时,实际摆角___5°(填“大于”或“小于”)。
(3)某次实验所用单摆的摆线长度为81.50 cm,则摆长为__ cm。实验中观测到从摆球第1次经过最低点到第61次经过最低点的时间间隔为54.60 s,则此单摆周期为___ s,该小组测得的重力加速度大小为__ m/s2。(结果均保留3位有效数字,π2取9.870)
7.(2023·湖南卷)某同学探究弹簧振子振动周期与质量的关系,实验装置如图(a)所示,轻质弹簧上端悬挂在铁架台上,下端挂有钩码,钩码下表面吸附一个小磁铁,其正下方放置智能手机,手机中的磁传感器可以采集磁感应强度实时变化的数据并输出图像,实验步骤如下:
(1)测出钩码和小磁铁的总质量m;
(2)在弹簧下端挂上该钩码和小磁铁,使弹簧振子在竖直方向做简谐运动,打开手机的磁传感器软件,此时磁传感器记录的磁感应强度变化周期等于弹簧振子振动周期;
(3)某次采集到的磁感应强度B的大小随时间t变化的图像如图(b)所示,从图中可以算出弹簧振子振动周期T= (用“t0”表示);
(4)改变钩码质量,重复上述步骤;
(5)实验测得数据如下表所示,分析数据可知,弹簧振子振动周期的平方与质量的关系是___(填“线性的”或“非线性的”);
m/kg 10T/s T/s T2/s2
0.015 2.43 0.243 0.059
0.025 3.14 0.314 0.099
0.035 3.72 0.372 0.138
0.045 4.22 0.422 0.178
0.055 4.66 0.466 0.217
(6)设弹簧的劲度系数为k,根据实验结果并结合物理量的单位关系,弹簧振子振动周期的表达式可能是___(填正确答案标号);
A.2π B.2π
C.2π D.2πk
(7)除偶然误差外,写出一条本实验中可能产生误差的原因:___。
8.(2021·河北卷,17)如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,2 s内经过的路程为0.4 m。该弹簧振子的周期为_4__s,振幅为_0.2__ m。
9.(2021·广东卷,17)如图所示,一个轻质弹簧下端挂一小球,小球静止。现将小球向下拉动距离A后由静止释放,并开始计时,小球在竖直方向做简谐运动,周期为T。经时间,小球从最低点向上运动的距离_小于__(选填“大于”“小于”或“等于”);在时刻,小球的动能_最大__(选填“最大”或“最小”)。
第2章 机械振动
一、高考真题探析
典 题 (2019·全国卷)如图,长为l的细绳下方悬挂一小球a。绳的另一端固定在天花板上O点处,在O点正下方l的O′处有一固定细铁钉。将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时。当小球a摆至最低位置时,细绳会受到铁钉的阻挡。设小球相对于其平衡位置的水平位移为x,向右为正。下列图像中,能描述小球在开始一个周期内的x-t关系的是( A )
解析:小球属于单摆模型,从右向左运动到平衡位置的过程,相当于运动第一个周期,根据单摆周期公式有t=×2π=,从平衡位置向左运动的过程中,相当于运动了第二个周期,有t′=×2π=,由此可知,第一个周期的时间长,第二个周期的时间短;结合位移来分析,设竖直位移最大值为h,第一个周期的水平位移最大值xm1==,第二个周期的水平位移最大值xm2==,可知xm1 > xm2,故选A。
二、临场真题练兵
1.(2022·湖南卷,16(1))下端附着重物的粗细均匀木棒,竖直浮在河面,在重力和浮力作用下,沿竖直方向做频率为1 Hz的简谐运动;与此同时,木棒在水平方向上随河水做匀速直线运动,如图(a)所示。以木棒所受浮力F为纵轴,木棒水平位移x为横轴建立直角坐标系,浮力F随水平位移x的变化如图(b)所示。已知河水密度为ρ,木棒横截面积为S,重力加速度大小为g。下列说法正确的是( ABD )
A.x从0.05 m到0.15 m的过程中,木棒的动能先增大后减小
B.x从0.21 m到0.25 m的过程中,木棒加速度方向竖直向下,大小逐渐变小
C.x=0.35 m和x=0.45 m时,木棒的速度大小相等,方向相反
D.木棒在竖直方向做简谐运动的振幅为
解析:木棒在竖直方向做简谐运动,浮力恰好等于重力时木棒速度最大,动能最大。根据浮力等于排开液体的重力、浮力随水平位移x变化的图像可知,x从0.05 m到0.15 m的过程中,木棒的速度先增大后减小,木棒的动能先增大后减小,选项A正确。x从0.21 m到0.25 m的过程中,木棒从平衡位置上方靠近最大位移处向下运动(未到平衡位置),加速度竖直向下,大小减小,选项B正确。x=0.35 m时,木棒向下运动,x=0.45 m时木棒在同一位置向上运动,x=0.35 m和x=0.45 m时,木棒在竖直方向的速度大小相等,方向相反,而两时刻木棒水平方向速度相同,所以合速度大小相等,方向不是相反,选项C错误。木棒底端处于水面下最大位移时,F1=ρgSh1,木棒底端处于水面下最小位移时,F2=ρgSh2,木棒在竖直方向做简谐运动的振幅A==,选项D正确。
2.(2022·浙江6月卷,11)如图所示,一根固定在墙上的水平光滑杆,两端分别固定着相同的轻弹簧,两弹簧自由端相距x。套上的小球从中点以初速度v向右运动,小球将做周期为T的往复运动,则( B )
A.小球做简谐运动
B.小球动能的变化周期为
C.两根弹簧的总弹性势能的变化周期为T
D.小球的初速度为时,其运动周期为2T
解析:由于刚开始的一段时间内小球做匀速运动,受力大小与位移大小不成正比,小球做的不是简谐运动,A错误;小球从杆中点到第一次回到杆中点的过程,初、末动能相等,则小球动能的变化周期为,分析可知两根弹簧的总弹性势能的变化周期也为,B正确,C错误;小球的初速度为时,在细杆上匀速运动的时间等于初速度为v时的2倍,小球从接触弹簧到速度减到零的时间等于初速度为v时的从接触弹簧到速度减为零的时间,故初速度为时的运动周期小于2T,D错误。
3.(2023·浙江卷)如图甲所示,一导体杆用两条等长细导线悬挂于水平轴OO′,接入电阻R构成回路。导体杆处于竖直向上的匀强磁场中,将导体杆从竖直位置拉开小角度由静止释放,导体杆开始下摆。当R=R0时,导体杆振动图像如图乙所示。若横纵坐标皆采用图乙标度,则当R=2R0时,导体杆振动图像是( B )
A B C D
解析:导体杆切割磁感线时,回路中产生感应电流,由楞次定律可得,导体杆受到的安培力总是阻碍导体棒的运动。当R从R0变为2R0时,回路中的电阻增大,则电流减小,导体杆所受安培力减小,即导体杆在摆动时所受的阻力减弱,所以杆从开始摆动到停止,运动的路程和经历的时间变长。
4.(2021·江苏卷)如图所示,半径为R的圆盘边缘有一钉子B,在水平光线下,圆盘的转轴A和钉子B在右侧墙壁上形成影子O和P,以O为原点在竖直方向上建立x坐标系。t=0时从图示位置沿逆时针方向匀速转动圆盘,角速度为ω,则P做简谐运动的表达式为( B )
A.x=Rsin
B.x=Rsin
C.x=2Rsin
D.x=2Rsin
解析:由图可知,影子P做简谐运动的振幅为R,以向上为正方向,设P的振动方程为x=Rsin (ωt+φ),由图可知,当t=0时,P的位移为R,代入振动方程解得φ=,则P做简谐运动的表达式为x=Rsin,故B正确,A、C、D错误。
5.(2023·重庆卷)某实验小组用单摆测量重力加速度。所用实验器材有摆球、长度可调的轻质摆线、刻度尺、50分度的游标卡尺、摄像装置等。
(1)用游标卡尺测量摆球直径d。当量爪并拢时,游标尺和主尺的零刻度线对齐。放置摆球后游标卡尺示数如图甲所示,则摆球的直径d为_19.20__ mm。
(2)用摆线和摆球组成单摆,如图乙所示。当摆线长度l=990.1 mm时,记录并分析单摆的振动视频,得到单摆的振动周期T=2.00 s,由此算得重力加速度g为_9.86__ m/s2(保留3位有效数字)。
(3)改变摆线长度l,记录并分析单摆的振动视频,得到相应的振动周期。他们发现,分别用l和l+作为摆长,这两种计算方法得到的重力加速度数值的差异大小Δg随摆线长度l的变化曲线如图所示。由图可知,该实验中,随着摆线长度l的增加,Δg的变化特点是_随着摆线长度l的增加,Δg逐渐减小__,原因是 随着摆线长度l的增加,则l+越接近于l,此时计算得到的g的差值越小 。
解析:(1)用游标卡尺测量摆球直径d=19 mm+0.02 mm×10=19.20 mm。
(2)单摆的摆长为L=990.1 mm+×19.20 mm=999.7 mm,根据T=2π,可得g=,带入数据g= m/s2=9.86 m/s2。
(3)由图可知,随着摆线长度l的增加,Δg逐渐减小,原因是随着摆线长度l的增加,则l+越接近于l,此时计算得到的g的差值越小。
6.(2023·山西卷)一学生小组做“用单摆测量重力加速度的大小”实验。
(1)用实验室提供的螺旋测微器测量摆球直径。首先,调节螺旋测微器,拧动微调旋钮使测微螺杆和测砧相触时,发现固定刻度的横线与可动刻度上的零刻度线未对齐,如图(a)所示,该示数为_0.006/0.007/0.008__ mm;螺旋测微器在夹有摆球时示数如图(b)所示,该示数为_20.034/20.033/20.035/20.032__ mm,则摆球的直径为_20.027/20.028/20.029__ mm。
(2)单摆实验的装置示意图如图(c)所示,其中角度盘需要固定在杆上的确定点O处,摆线在角度盘上所指的示数为摆角的大小。若将角度盘固定在O点上方,则摆线在角度盘上所指的示数为5°时,实际摆角_大于__5°(填“大于”或“小于”)。
(3)某次实验所用单摆的摆线长度为81.50 cm,则摆长为_82.5__ cm。实验中观测到从摆球第1次经过最低点到第61次经过最低点的时间间隔为54.60 s,则此单摆周期为_1.82__ s,该小组测得的重力加速度大小为_9.83__ m/s2。(结果均保留3位有效数字,π2取9.870)
解析:(1)测量前测微螺杆与和测砧相触时,图(a)的示数为d0=0 mm+0.7×0.01 mm=0.007 mm,螺旋测微器读数是固定刻度读数(0.5 mm的整数倍)加可动刻度(0.5 mm以下的小数)读数,图中读数为d1=20 mm+3.4×0.01 mm=20.034 mm,
则摆球的直径为d=d1-d0=20.027 mm。
(2)角度盘的大小一定,即在规定的位置安装角度盘,测量的摆角准确,但将角度盘固定在规定位置上方,即角度盘到悬挂点的距离变短,同样的角度,摆线在刻度盘上扫过的弧长变短,故摆线在角度盘上所指的示数为5°时,实际摆角大于5°。
(3)单摆的摆线长度为81.50 cm,则摆长为l=l0+=81.50 cm+ cm=82.5 cm,
结果保留三位有效数字,得摆长为82.5 cm;一次全振动单摆经过最低点两次,故此单摆的周期为T== s=1.82 s,由单摆的周期表达式T=2π得,重力加速度g==9.83 m/s2。
7.(2023·湖南卷)某同学探究弹簧振子振动周期与质量的关系,实验装置如图(a)所示,轻质弹簧上端悬挂在铁架台上,下端挂有钩码,钩码下表面吸附一个小磁铁,其正下方放置智能手机,手机中的磁传感器可以采集磁感应强度实时变化的数据并输出图像,实验步骤如下:
(1)测出钩码和小磁铁的总质量m;
(2)在弹簧下端挂上该钩码和小磁铁,使弹簧振子在竖直方向做简谐运动,打开手机的磁传感器软件,此时磁传感器记录的磁感应强度变化周期等于弹簧振子振动周期;
(3)某次采集到的磁感应强度B的大小随时间t变化的图像如图(b)所示,从图中可以算出弹簧振子振动周期T= (用“t0”表示);
(4)改变钩码质量,重复上述步骤;
(5)实验测得数据如下表所示,分析数据可知,弹簧振子振动周期的平方与质量的关系是_线性的__(填“线性的”或“非线性的”);
m/kg 10T/s T/s T2/s2
0.015 2.43 0.243 0.059
0.025 3.14 0.314 0.099
0.035 3.72 0.372 0.138
0.045 4.22 0.422 0.178
0.055 4.66 0.466 0.217
(6)设弹簧的劲度系数为k,根据实验结果并结合物理量的单位关系,弹簧振子振动周期的表达式可能是_A__(填正确答案标号);
A.2π B.2π
C.2π D.2πk
(7)除偶然误差外,写出一条本实验中可能产生误差的原因:_空气阻力__。
解析:(3)从图中可以算出弹簧振子振动周期T=。
(5)分析数据可知,弹簧振子振动周期的平方与质量的比值接近于常量3.95,则弹簧振子振动周期的平方与质量的关系是线性的。
(6)因2π的单位为==s,因为s(秒)为周期的单位,则其他各项单位都不是周期的单位,故选A。
(7)除偶然误差外,钩码振动过程中受空气阻力的影响可能会使本实验产生误差。
8.(2021·河北卷,17)如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,2 s内经过的路程为0.4 m。该弹簧振子的周期为_4__s,振幅为_0.2__ m。
解析:根据简谐运动对称性可知,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,则A、B两点关于平衡位置对称,而振动经过了半个周期的运动,则周期为T=2t=4 s,从A到B经过了半个周期的振动,路程为s=0.4 m,而一个完整的周期路程为0.8 m,为4个振幅的路程,有4A=0.8 m,解得振幅为A=0.2 m。
9.(2021·广东卷,17)如图所示,一个轻质弹簧下端挂一小球,小球静止。现将小球向下拉动距离A后由静止释放,并开始计时,小球在竖直方向做简谐运动,周期为T。经时间,小球从最低点向上运动的距离_小于__(选填“大于”“小于”或“等于”);在时刻,小球的动能_最大__(选填“最大”或“最小”)。
解析:根据简谐振动的位移公式y=-Acos,则t=时有y=-Acos=-A,所以小球从最低点向上运动的距离为Δy=A-A=A
一、高考真题探析
典 题 (2019·全国卷)如图,长为l的细绳下方悬挂一小球a。绳的另一端固定在天花板上O点处,在O点正下方l的O′处有一固定细铁钉。将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时。当小球a摆至最低位置时,细绳会受到铁钉的阻挡。设小球相对于其平衡位置的水平位移为x,向右为正。下列图像中,能描述小球在开始一个周期内的x-t关系的是( )
二、临场真题练兵
1.(2022·湖南卷,16(1))下端附着重物的粗细均匀木棒,竖直浮在河面,在重力和浮力作用下,沿竖直方向做频率为1 Hz的简谐运动;与此同时,木棒在水平方向上随河水做匀速直线运动,如图(a)所示。以木棒所受浮力F为纵轴,木棒水平位移x为横轴建立直角坐标系,浮力F随水平位移x的变化如图(b)所示。已知河水密度为ρ,木棒横截面积为S,重力加速度大小为g。下列说法正确的是( )
A.x从0.05 m到0.15 m的过程中,木棒的动能先增大后减小
B.x从0.21 m到0.25 m的过程中,木棒加速度方向竖直向下,大小逐渐变小
C.x=0.35 m和x=0.45 m时,木棒的速度大小相等,方向相反
D.木棒在竖直方向做简谐运动的振幅为
2.(2022·浙江6月卷,11)如图所示,一根固定在墙上的水平光滑杆,两端分别固定着相同的轻弹簧,两弹簧自由端相距x。套上的小球从中点以初速度v向右运动,小球将做周期为T的往复运动,则( )
A.小球做简谐运动
B.小球动能的变化周期为
C.两根弹簧的总弹性势能的变化周期为T
D.小球的初速度为时,其运动周期为2T
3.(2023·浙江卷)如图甲所示,一导体杆用两条等长细导线悬挂于水平轴OO′,接入电阻R构成回路。导体杆处于竖直向上的匀强磁场中,将导体杆从竖直位置拉开小角度由静止释放,导体杆开始下摆。当R=R0时,导体杆振动图像如图乙所示。若横纵坐标皆采用图乙标度,则当R=2R0时,导体杆振动图像是( )
A B C D
4.(2021·江苏卷)如图所示,半径为R的圆盘边缘有一钉子B,在水平光线下,圆盘的转轴A和钉子B在右侧墙壁上形成影子O和P,以O为原点在竖直方向上建立x坐标系。t=0时从图示位置沿逆时针方向匀速转动圆盘,角速度为ω,则P做简谐运动的表达式为( )
A.x=Rsin
B.x=Rsin
C.x=2Rsin
D.x=2Rsin
5.(2023·重庆卷)某实验小组用单摆测量重力加速度。所用实验器材有摆球、长度可调的轻质摆线、刻度尺、50分度的游标卡尺、摄像装置等。
(1)用游标卡尺测量摆球直径d。当量爪并拢时,游标尺和主尺的零刻度线对齐。放置摆球后游标卡尺示数如图甲所示,则摆球的直径d为___ mm。
(2)用摆线和摆球组成单摆,如图乙所示。当摆线长度l=990.1 mm时,记录并分析单摆的振动视频,得到单摆的振动周期T=2.00 s,由此算得重力加速度g为___ m/s2(保留3位有效数字)。
(3)改变摆线长度l,记录并分析单摆的振动视频,得到相应的振动周期。他们发现,分别用l和l+作为摆长,这两种计算方法得到的重力加速度数值的差异大小Δg随摆线长度l的变化曲线如图所示。由图可知,该实验中,随着摆线长度l的增加,Δg的变化特点是___,原因是 。
6.(2023·山西卷)一学生小组做“用单摆测量重力加速度的大小”实验。
(1)用实验室提供的螺旋测微器测量摆球直径。首先,调节螺旋测微器,拧动微调旋钮使测微螺杆和测砧相触时,发现固定刻度的横线与可动刻度上的零刻度线未对齐,如图(a)所示,该示数为___ mm;螺旋测微器在夹有摆球时示数如图(b)所示,该示数为___ mm,则摆球的直径为___ mm。
(2)单摆实验的装置示意图如图(c)所示,其中角度盘需要固定在杆上的确定点O处,摆线在角度盘上所指的示数为摆角的大小。若将角度盘固定在O点上方,则摆线在角度盘上所指的示数为5°时,实际摆角___5°(填“大于”或“小于”)。
(3)某次实验所用单摆的摆线长度为81.50 cm,则摆长为__ cm。实验中观测到从摆球第1次经过最低点到第61次经过最低点的时间间隔为54.60 s,则此单摆周期为___ s,该小组测得的重力加速度大小为__ m/s2。(结果均保留3位有效数字,π2取9.870)
7.(2023·湖南卷)某同学探究弹簧振子振动周期与质量的关系,实验装置如图(a)所示,轻质弹簧上端悬挂在铁架台上,下端挂有钩码,钩码下表面吸附一个小磁铁,其正下方放置智能手机,手机中的磁传感器可以采集磁感应强度实时变化的数据并输出图像,实验步骤如下:
(1)测出钩码和小磁铁的总质量m;
(2)在弹簧下端挂上该钩码和小磁铁,使弹簧振子在竖直方向做简谐运动,打开手机的磁传感器软件,此时磁传感器记录的磁感应强度变化周期等于弹簧振子振动周期;
(3)某次采集到的磁感应强度B的大小随时间t变化的图像如图(b)所示,从图中可以算出弹簧振子振动周期T= (用“t0”表示);
(4)改变钩码质量,重复上述步骤;
(5)实验测得数据如下表所示,分析数据可知,弹簧振子振动周期的平方与质量的关系是___(填“线性的”或“非线性的”);
m/kg 10T/s T/s T2/s2
0.015 2.43 0.243 0.059
0.025 3.14 0.314 0.099
0.035 3.72 0.372 0.138
0.045 4.22 0.422 0.178
0.055 4.66 0.466 0.217
(6)设弹簧的劲度系数为k,根据实验结果并结合物理量的单位关系,弹簧振子振动周期的表达式可能是___(填正确答案标号);
A.2π B.2π
C.2π D.2πk
(7)除偶然误差外,写出一条本实验中可能产生误差的原因:___。
8.(2021·河北卷,17)如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,2 s内经过的路程为0.4 m。该弹簧振子的周期为_4__s,振幅为_0.2__ m。
9.(2021·广东卷,17)如图所示,一个轻质弹簧下端挂一小球,小球静止。现将小球向下拉动距离A后由静止释放,并开始计时,小球在竖直方向做简谐运动,周期为T。经时间,小球从最低点向上运动的距离_小于__(选填“大于”“小于”或“等于”);在时刻,小球的动能_最大__(选填“最大”或“最小”)。
第2章 机械振动
一、高考真题探析
典 题 (2019·全国卷)如图,长为l的细绳下方悬挂一小球a。绳的另一端固定在天花板上O点处,在O点正下方l的O′处有一固定细铁钉。将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时。当小球a摆至最低位置时,细绳会受到铁钉的阻挡。设小球相对于其平衡位置的水平位移为x,向右为正。下列图像中,能描述小球在开始一个周期内的x-t关系的是( A )
解析:小球属于单摆模型,从右向左运动到平衡位置的过程,相当于运动第一个周期,根据单摆周期公式有t=×2π=,从平衡位置向左运动的过程中,相当于运动了第二个周期,有t′=×2π=,由此可知,第一个周期的时间长,第二个周期的时间短;结合位移来分析,设竖直位移最大值为h,第一个周期的水平位移最大值xm1==,第二个周期的水平位移最大值xm2==,可知xm1 > xm2,故选A。
二、临场真题练兵
1.(2022·湖南卷,16(1))下端附着重物的粗细均匀木棒,竖直浮在河面,在重力和浮力作用下,沿竖直方向做频率为1 Hz的简谐运动;与此同时,木棒在水平方向上随河水做匀速直线运动,如图(a)所示。以木棒所受浮力F为纵轴,木棒水平位移x为横轴建立直角坐标系,浮力F随水平位移x的变化如图(b)所示。已知河水密度为ρ,木棒横截面积为S,重力加速度大小为g。下列说法正确的是( ABD )
A.x从0.05 m到0.15 m的过程中,木棒的动能先增大后减小
B.x从0.21 m到0.25 m的过程中,木棒加速度方向竖直向下,大小逐渐变小
C.x=0.35 m和x=0.45 m时,木棒的速度大小相等,方向相反
D.木棒在竖直方向做简谐运动的振幅为
解析:木棒在竖直方向做简谐运动,浮力恰好等于重力时木棒速度最大,动能最大。根据浮力等于排开液体的重力、浮力随水平位移x变化的图像可知,x从0.05 m到0.15 m的过程中,木棒的速度先增大后减小,木棒的动能先增大后减小,选项A正确。x从0.21 m到0.25 m的过程中,木棒从平衡位置上方靠近最大位移处向下运动(未到平衡位置),加速度竖直向下,大小减小,选项B正确。x=0.35 m时,木棒向下运动,x=0.45 m时木棒在同一位置向上运动,x=0.35 m和x=0.45 m时,木棒在竖直方向的速度大小相等,方向相反,而两时刻木棒水平方向速度相同,所以合速度大小相等,方向不是相反,选项C错误。木棒底端处于水面下最大位移时,F1=ρgSh1,木棒底端处于水面下最小位移时,F2=ρgSh2,木棒在竖直方向做简谐运动的振幅A==,选项D正确。
2.(2022·浙江6月卷,11)如图所示,一根固定在墙上的水平光滑杆,两端分别固定着相同的轻弹簧,两弹簧自由端相距x。套上的小球从中点以初速度v向右运动,小球将做周期为T的往复运动,则( B )
A.小球做简谐运动
B.小球动能的变化周期为
C.两根弹簧的总弹性势能的变化周期为T
D.小球的初速度为时,其运动周期为2T
解析:由于刚开始的一段时间内小球做匀速运动,受力大小与位移大小不成正比,小球做的不是简谐运动,A错误;小球从杆中点到第一次回到杆中点的过程,初、末动能相等,则小球动能的变化周期为,分析可知两根弹簧的总弹性势能的变化周期也为,B正确,C错误;小球的初速度为时,在细杆上匀速运动的时间等于初速度为v时的2倍,小球从接触弹簧到速度减到零的时间等于初速度为v时的从接触弹簧到速度减为零的时间,故初速度为时的运动周期小于2T,D错误。
3.(2023·浙江卷)如图甲所示,一导体杆用两条等长细导线悬挂于水平轴OO′,接入电阻R构成回路。导体杆处于竖直向上的匀强磁场中,将导体杆从竖直位置拉开小角度由静止释放,导体杆开始下摆。当R=R0时,导体杆振动图像如图乙所示。若横纵坐标皆采用图乙标度,则当R=2R0时,导体杆振动图像是( B )
A B C D
解析:导体杆切割磁感线时,回路中产生感应电流,由楞次定律可得,导体杆受到的安培力总是阻碍导体棒的运动。当R从R0变为2R0时,回路中的电阻增大,则电流减小,导体杆所受安培力减小,即导体杆在摆动时所受的阻力减弱,所以杆从开始摆动到停止,运动的路程和经历的时间变长。
4.(2021·江苏卷)如图所示,半径为R的圆盘边缘有一钉子B,在水平光线下,圆盘的转轴A和钉子B在右侧墙壁上形成影子O和P,以O为原点在竖直方向上建立x坐标系。t=0时从图示位置沿逆时针方向匀速转动圆盘,角速度为ω,则P做简谐运动的表达式为( B )
A.x=Rsin
B.x=Rsin
C.x=2Rsin
D.x=2Rsin
解析:由图可知,影子P做简谐运动的振幅为R,以向上为正方向,设P的振动方程为x=Rsin (ωt+φ),由图可知,当t=0时,P的位移为R,代入振动方程解得φ=,则P做简谐运动的表达式为x=Rsin,故B正确,A、C、D错误。
5.(2023·重庆卷)某实验小组用单摆测量重力加速度。所用实验器材有摆球、长度可调的轻质摆线、刻度尺、50分度的游标卡尺、摄像装置等。
(1)用游标卡尺测量摆球直径d。当量爪并拢时,游标尺和主尺的零刻度线对齐。放置摆球后游标卡尺示数如图甲所示,则摆球的直径d为_19.20__ mm。
(2)用摆线和摆球组成单摆,如图乙所示。当摆线长度l=990.1 mm时,记录并分析单摆的振动视频,得到单摆的振动周期T=2.00 s,由此算得重力加速度g为_9.86__ m/s2(保留3位有效数字)。
(3)改变摆线长度l,记录并分析单摆的振动视频,得到相应的振动周期。他们发现,分别用l和l+作为摆长,这两种计算方法得到的重力加速度数值的差异大小Δg随摆线长度l的变化曲线如图所示。由图可知,该实验中,随着摆线长度l的增加,Δg的变化特点是_随着摆线长度l的增加,Δg逐渐减小__,原因是 随着摆线长度l的增加,则l+越接近于l,此时计算得到的g的差值越小 。
解析:(1)用游标卡尺测量摆球直径d=19 mm+0.02 mm×10=19.20 mm。
(2)单摆的摆长为L=990.1 mm+×19.20 mm=999.7 mm,根据T=2π,可得g=,带入数据g= m/s2=9.86 m/s2。
(3)由图可知,随着摆线长度l的增加,Δg逐渐减小,原因是随着摆线长度l的增加,则l+越接近于l,此时计算得到的g的差值越小。
6.(2023·山西卷)一学生小组做“用单摆测量重力加速度的大小”实验。
(1)用实验室提供的螺旋测微器测量摆球直径。首先,调节螺旋测微器,拧动微调旋钮使测微螺杆和测砧相触时,发现固定刻度的横线与可动刻度上的零刻度线未对齐,如图(a)所示,该示数为_0.006/0.007/0.008__ mm;螺旋测微器在夹有摆球时示数如图(b)所示,该示数为_20.034/20.033/20.035/20.032__ mm,则摆球的直径为_20.027/20.028/20.029__ mm。
(2)单摆实验的装置示意图如图(c)所示,其中角度盘需要固定在杆上的确定点O处,摆线在角度盘上所指的示数为摆角的大小。若将角度盘固定在O点上方,则摆线在角度盘上所指的示数为5°时,实际摆角_大于__5°(填“大于”或“小于”)。
(3)某次实验所用单摆的摆线长度为81.50 cm,则摆长为_82.5__ cm。实验中观测到从摆球第1次经过最低点到第61次经过最低点的时间间隔为54.60 s,则此单摆周期为_1.82__ s,该小组测得的重力加速度大小为_9.83__ m/s2。(结果均保留3位有效数字,π2取9.870)
解析:(1)测量前测微螺杆与和测砧相触时,图(a)的示数为d0=0 mm+0.7×0.01 mm=0.007 mm,螺旋测微器读数是固定刻度读数(0.5 mm的整数倍)加可动刻度(0.5 mm以下的小数)读数,图中读数为d1=20 mm+3.4×0.01 mm=20.034 mm,
则摆球的直径为d=d1-d0=20.027 mm。
(2)角度盘的大小一定,即在规定的位置安装角度盘,测量的摆角准确,但将角度盘固定在规定位置上方,即角度盘到悬挂点的距离变短,同样的角度,摆线在刻度盘上扫过的弧长变短,故摆线在角度盘上所指的示数为5°时,实际摆角大于5°。
(3)单摆的摆线长度为81.50 cm,则摆长为l=l0+=81.50 cm+ cm=82.5 cm,
结果保留三位有效数字,得摆长为82.5 cm;一次全振动单摆经过最低点两次,故此单摆的周期为T== s=1.82 s,由单摆的周期表达式T=2π得,重力加速度g==9.83 m/s2。
7.(2023·湖南卷)某同学探究弹簧振子振动周期与质量的关系,实验装置如图(a)所示,轻质弹簧上端悬挂在铁架台上,下端挂有钩码,钩码下表面吸附一个小磁铁,其正下方放置智能手机,手机中的磁传感器可以采集磁感应强度实时变化的数据并输出图像,实验步骤如下:
(1)测出钩码和小磁铁的总质量m;
(2)在弹簧下端挂上该钩码和小磁铁,使弹簧振子在竖直方向做简谐运动,打开手机的磁传感器软件,此时磁传感器记录的磁感应强度变化周期等于弹簧振子振动周期;
(3)某次采集到的磁感应强度B的大小随时间t变化的图像如图(b)所示,从图中可以算出弹簧振子振动周期T= (用“t0”表示);
(4)改变钩码质量,重复上述步骤;
(5)实验测得数据如下表所示,分析数据可知,弹簧振子振动周期的平方与质量的关系是_线性的__(填“线性的”或“非线性的”);
m/kg 10T/s T/s T2/s2
0.015 2.43 0.243 0.059
0.025 3.14 0.314 0.099
0.035 3.72 0.372 0.138
0.045 4.22 0.422 0.178
0.055 4.66 0.466 0.217
(6)设弹簧的劲度系数为k,根据实验结果并结合物理量的单位关系,弹簧振子振动周期的表达式可能是_A__(填正确答案标号);
A.2π B.2π
C.2π D.2πk
(7)除偶然误差外,写出一条本实验中可能产生误差的原因:_空气阻力__。
解析:(3)从图中可以算出弹簧振子振动周期T=。
(5)分析数据可知,弹簧振子振动周期的平方与质量的比值接近于常量3.95,则弹簧振子振动周期的平方与质量的关系是线性的。
(6)因2π的单位为==s,因为s(秒)为周期的单位,则其他各项单位都不是周期的单位,故选A。
(7)除偶然误差外,钩码振动过程中受空气阻力的影响可能会使本实验产生误差。
8.(2021·河北卷,17)如图,一弹簧振子沿x轴做简谐运动,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,2 s内经过的路程为0.4 m。该弹簧振子的周期为_4__s,振幅为_0.2__ m。
解析:根据简谐运动对称性可知,振子零时刻向右经过A点,2 s后第一次到达B点,已知振子经过A、B两点时的速度大小相等,则A、B两点关于平衡位置对称,而振动经过了半个周期的运动,则周期为T=2t=4 s,从A到B经过了半个周期的振动,路程为s=0.4 m,而一个完整的周期路程为0.8 m,为4个振幅的路程,有4A=0.8 m,解得振幅为A=0.2 m。
9.(2021·广东卷,17)如图所示,一个轻质弹簧下端挂一小球,小球静止。现将小球向下拉动距离A后由静止释放,并开始计时,小球在竖直方向做简谐运动,周期为T。经时间,小球从最低点向上运动的距离_小于__(选填“大于”“小于”或“等于”);在时刻,小球的动能_最大__(选填“最大”或“最小”)。
解析:根据简谐振动的位移公式y=-Acos,则t=时有y=-Acos=-A,所以小球从最低点向上运动的距离为Δy=A-A=A
