北师大版六年级数学下册 一 圆柱和圆锥_ 圆柱的体积 课件(共28张PPT)
文档属性
| 名称 | 北师大版六年级数学下册 一 圆柱和圆锥_ 圆柱的体积 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-10 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
北师大版六年级数学第十二册
圆柱的体积
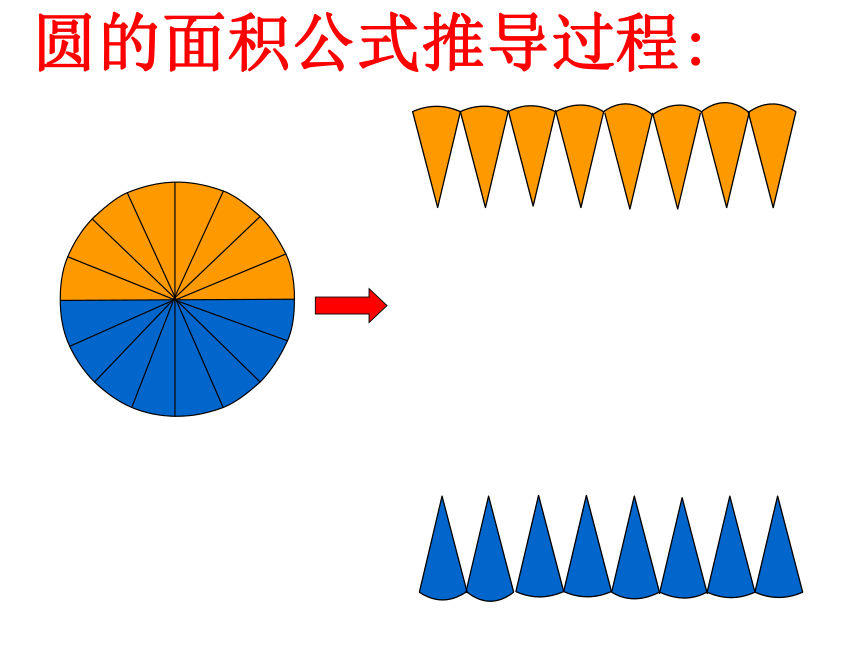
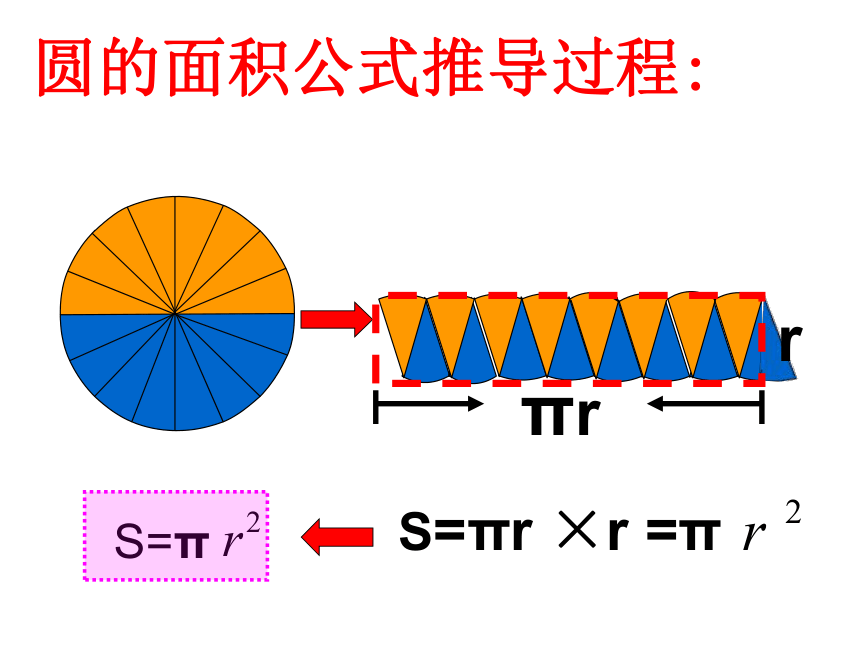
圆的面积公式推导过程:
πr
r
S=πr ×r =π
S=π
圆的面积公式推导过程:
怎样求它们的体积呢
学习目标
1.结合具体情境和实践活动,了解圆柱体积和容积的含义。
2.经历“类比猜想——验证说明”的探索圆柱体积计算方法的过程。渗透转化的思想方法。掌握圆柱体积的计算方法。
3.会运用圆柱体积的知识解决一些简单的实际问题。
观察与思考
观察教材第8页的内容,说一说
什么是圆柱的体积?什么是圆
柱的容积?
思考并回答
你能猜测怎样计算圆柱的体积
吗?说一说猜测理由?
长方体的体积=长×宽×高
V = sh
h
a
b
底面积
正方体的体积=棱长×棱长×棱长
V = sh
a
底面积
a
a
V =s h
直柱体的体积 = 底面积×高
自学﹑小组合作学习
按照教材所说的方法,尝试验证
你的猜想。
小结:圆柱体的体积与它的底面积和高有关系
当圆柱的底面积一定时,圆柱的高越
高,体积就越大,高越矮,体积就越小。
当圆柱的高一定时,圆柱的底面积越
大,体积就越大。底面积越小,体积就
越小。
总结:
圆柱的体积=底面积×高
V=Sh
一、填表。
底面积 s
(平方米) 高 h
(米) 圆柱体积 V
(立方米)
15
3
45
40
4
160
二、填空
1、一个长方体和一个圆柱的体积
相等,高也相等,那么它们的
底面积( )。
2、一根横截面面积是10平方厘米
的圆柱形钢材,长是2米,它的
体积是( )立方厘米。
相等
2000
三、判断对错。
1、圆柱体体积与长方体体积相等。
( )
2、长方体、正方体、圆柱体的体积都
可以用底面积乘高的方法来计算。
( )
×
√
3、圆柱体的底面积越大,它的
体积越大。
( )
4、圆柱体的高越长,它的体积越
大。
( )
×
×
圆柱体积公式的应用
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
V=πr h
V=π(d÷2) h
V=π(C÷π÷2) h
3.14 ×0.42×5=2.512(立方米)
答:它的体积是2.512立方米。
求圆柱体积必备的条件有两个:
一个是它的底面积
第二个是它的高
练 习
完成教材第9页练一练的题目
求圆柱的容积
圆柱的容积怎样计算?
圆柱的体积与容积什么异同吗?
圆柱体容积公式
圆柱的容积=底面积×高
V=Sh
圆柱形容器容积和体积的异同点
相同点:计算方法相同。
不同点:1、计量单位不同。
2、测量数据的方法不同。
分享收获!
寻找生活中的圆柱形物体,
测量出相关数据,并计算出体积。
作业:
1、暮色苍茫,皎洁的明月升上了天空,银色的月光透过松树的虬枝翠叶,星星点点地洒落下来。清清的泉水淙淙地流泻于山石之上,在月光辉映之下,宛若一条洁白的绸布闪闪发光
2、竹林里传来一阵银铃般的笑声,那是一群勤劳淳朴的山村姑娘刚洗完衣服,披着月光笑盈盈地归来了,也许她们正为什么开心的事儿在竹林里嬉戏追逐着,笑闹声传出翠竹林外。密密的荷叶纷纷倒向两旁,莲花摇动,水波荡漾,原来是顺流而下的渔舟正轻盈地穿过荷花丛,弄乱的荷塘月色,划破了大山的宁静。
3、空山雨后的秋凉,松间明月的清光,石上清泉的声音,浣衣村女的笑声,渔舟穿过荷丛的动态,和谐完美地融合在一起,有声有色,有景有人,有静有动,构成了空山秋天恬静幽美的乡村生活图景。
4.通过诗一般景物的描写,反映了诗人过安静淳朴生活的理想和对污浊官场的厌恶。诗中以物芳而明志洁,以人和而望政通。泉水、青松、翠竹、青莲,可以说是诗人高尚情操的写照,也是为诗人理想境界的环境烘托。
5、贵族子弟的通称,这里借指诗人自己。诗人曾为王孙、来自官场,而今隐居山间;表达了诗人寄情山水田园,对隐居生活怡然自得的满足心情,也是他高洁品质的写照。
6.人的一生,绝大部分时间都是在家庭中度过的。家庭不仅为人的生存发展提供基本物质保障,而且也为人的精神生活提供重要环境。人生的幸福很大程度上可归结为家庭的幸福。
7.放回原文,查对正误。特别是在时间、地点、官职,人物的行为、实效方面,应仔细查对原文的词句,全面理解,综合分析,两者间的差别正是把握全文的关键所在。对似是而非处,要有借题解文的意识。
8. 整首诗歌体现的并不是在秋色里持续的的消沉,而是在一片肃杀的秋景之中强调一种高洁的人品。
北师大版六年级数学第十二册
圆柱的体积
圆的面积公式推导过程:
πr
r
S=πr ×r =π
S=π
圆的面积公式推导过程:
怎样求它们的体积呢
学习目标
1.结合具体情境和实践活动,了解圆柱体积和容积的含义。
2.经历“类比猜想——验证说明”的探索圆柱体积计算方法的过程。渗透转化的思想方法。掌握圆柱体积的计算方法。
3.会运用圆柱体积的知识解决一些简单的实际问题。
观察与思考
观察教材第8页的内容,说一说
什么是圆柱的体积?什么是圆
柱的容积?
思考并回答
你能猜测怎样计算圆柱的体积
吗?说一说猜测理由?
长方体的体积=长×宽×高
V = sh
h
a
b
底面积
正方体的体积=棱长×棱长×棱长
V = sh
a
底面积
a
a
V =s h
直柱体的体积 = 底面积×高
自学﹑小组合作学习
按照教材所说的方法,尝试验证
你的猜想。
小结:圆柱体的体积与它的底面积和高有关系
当圆柱的底面积一定时,圆柱的高越
高,体积就越大,高越矮,体积就越小。
当圆柱的高一定时,圆柱的底面积越
大,体积就越大。底面积越小,体积就
越小。
总结:
圆柱的体积=底面积×高
V=Sh
一、填表。
底面积 s
(平方米) 高 h
(米) 圆柱体积 V
(立方米)
15
3
45
40
4
160
二、填空
1、一个长方体和一个圆柱的体积
相等,高也相等,那么它们的
底面积( )。
2、一根横截面面积是10平方厘米
的圆柱形钢材,长是2米,它的
体积是( )立方厘米。
相等
2000
三、判断对错。
1、圆柱体体积与长方体体积相等。
( )
2、长方体、正方体、圆柱体的体积都
可以用底面积乘高的方法来计算。
( )
×
√
3、圆柱体的底面积越大,它的
体积越大。
( )
4、圆柱体的高越长,它的体积越
大。
( )
×
×
圆柱体积公式的应用
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
V=πr h
V=π(d÷2) h
V=π(C÷π÷2) h
3.14 ×0.42×5=2.512(立方米)
答:它的体积是2.512立方米。
求圆柱体积必备的条件有两个:
一个是它的底面积
第二个是它的高
练 习
完成教材第9页练一练的题目
求圆柱的容积
圆柱的容积怎样计算?
圆柱的体积与容积什么异同吗?
圆柱体容积公式
圆柱的容积=底面积×高
V=Sh
圆柱形容器容积和体积的异同点
相同点:计算方法相同。
不同点:1、计量单位不同。
2、测量数据的方法不同。
分享收获!
寻找生活中的圆柱形物体,
测量出相关数据,并计算出体积。
作业:
1、暮色苍茫,皎洁的明月升上了天空,银色的月光透过松树的虬枝翠叶,星星点点地洒落下来。清清的泉水淙淙地流泻于山石之上,在月光辉映之下,宛若一条洁白的绸布闪闪发光
2、竹林里传来一阵银铃般的笑声,那是一群勤劳淳朴的山村姑娘刚洗完衣服,披着月光笑盈盈地归来了,也许她们正为什么开心的事儿在竹林里嬉戏追逐着,笑闹声传出翠竹林外。密密的荷叶纷纷倒向两旁,莲花摇动,水波荡漾,原来是顺流而下的渔舟正轻盈地穿过荷花丛,弄乱的荷塘月色,划破了大山的宁静。
3、空山雨后的秋凉,松间明月的清光,石上清泉的声音,浣衣村女的笑声,渔舟穿过荷丛的动态,和谐完美地融合在一起,有声有色,有景有人,有静有动,构成了空山秋天恬静幽美的乡村生活图景。
4.通过诗一般景物的描写,反映了诗人过安静淳朴生活的理想和对污浊官场的厌恶。诗中以物芳而明志洁,以人和而望政通。泉水、青松、翠竹、青莲,可以说是诗人高尚情操的写照,也是为诗人理想境界的环境烘托。
5、贵族子弟的通称,这里借指诗人自己。诗人曾为王孙、来自官场,而今隐居山间;表达了诗人寄情山水田园,对隐居生活怡然自得的满足心情,也是他高洁品质的写照。
6.人的一生,绝大部分时间都是在家庭中度过的。家庭不仅为人的生存发展提供基本物质保障,而且也为人的精神生活提供重要环境。人生的幸福很大程度上可归结为家庭的幸福。
7.放回原文,查对正误。特别是在时间、地点、官职,人物的行为、实效方面,应仔细查对原文的词句,全面理解,综合分析,两者间的差别正是把握全文的关键所在。对似是而非处,要有借题解文的意识。
8. 整首诗歌体现的并不是在秋色里持续的的消沉,而是在一片肃杀的秋景之中强调一种高洁的人品。
