2024年安徽省淮安市九年级中考数学一模错题集强化训练(含解析 )
文档属性
| 名称 | 2024年安徽省淮安市九年级中考数学一模错题集强化训练(含解析 ) |

|
|
| 格式 | doc | ||
| 文件大小 | 603.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 00:00:00 | ||
图片预览




文档简介
2023-2024学年淮安初三数学下一模错题集强化训练
一.选择题(共4小题)
1.(2023 淮安二模)如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的面积是( )
A.48 B.40 C.24 D.20
2.(2022 乌鲁木齐)一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )
A.x<2 B.x<0 C.x>0 D.x>2
3.(2020 攀枝花)若关于x的方程x2﹣x﹣m=0没有实数根,则m的值可以为( )
A.﹣1 B.﹣ C.0 D.1
4.(2022 乐山)关于x的一元二次方程3x2﹣2x+m=0有两根,其中一根为x=1,则这两根之积为( )
A. B. C.1 D.﹣
二.填空题(共5小题)
5.(2024 涟水县模拟)对于实数a、b,定义新运算“ ”:a b=a2﹣ab,如4 2=42﹣4×2=8.若x 4=﹣4,则实数x的值是 .
6.(2021 浙江)如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为 .
7.(2024 涟水县模拟)若圆锥的侧面积为25π,底面半径为5,则该圆锥的母线长是 .
8.(2022 临沂)比较大小: (填“>”,“<”或“=”).
9.(2022 毕节市)如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ长度的最小值为 .
三.解答题(共9小题)
10.(2023 淮安二模)如图,已知AB是⊙O的弦,C为⊙O上一点,∠C=∠BAD.
(1)请判断AD是否为⊙O的切线,并证明你的结论;
(2)若BD⊥AB于点B,AD=9,BD=6,求⊙O半径.
11.(2023 淮安二模)某网店专门销售某种品牌的笔筒,成本为20元/件,每天销售量y(件)与销售单价x(元)之间存在一次函数关系,如图,其中规定每天笔筒的销售量不低于210件.
(1)写出y与x之间的函数关系式 ;
(2)当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
12.(2023 淮安二模)我们知道,三角形的中位线平行于三角形的第三边,并且等于第三边的一半,如何证明三角形中位线定理呢?
(1)【方法回顾】
证明:三角形中位线定理.
已知:如图,在△ABC中,D、E分别是AB、AC的中点.
求证:DE∥BC,.
证明三角形中位线性质定理的方法很多,但多数都需要通过添加辅助线构图去完成,下面是其中一种证法的添加辅助线方法,阅读并完成填空:
添加辅助线,如图1,在△ABC中,过点C作CF∥AB,与DE的延长线交于点F.可证△ADE≌ ,根据全等三角形对应边相等可得DE=EF,然后判断出四边形BCFD是 ,根据图形性质可证得DE∥BC,.
(2)【方法迁移】
如图2,在四边形ABCD中,AD∥BC,∠A=90°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若,DF=4,∠GEF=90°,求GF的长.
(3)【定理应用】
如图3,在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,,延长BC至点E,使DE=DG,延长ED交AB于点F,直接写出的值(用含K的式子表示).
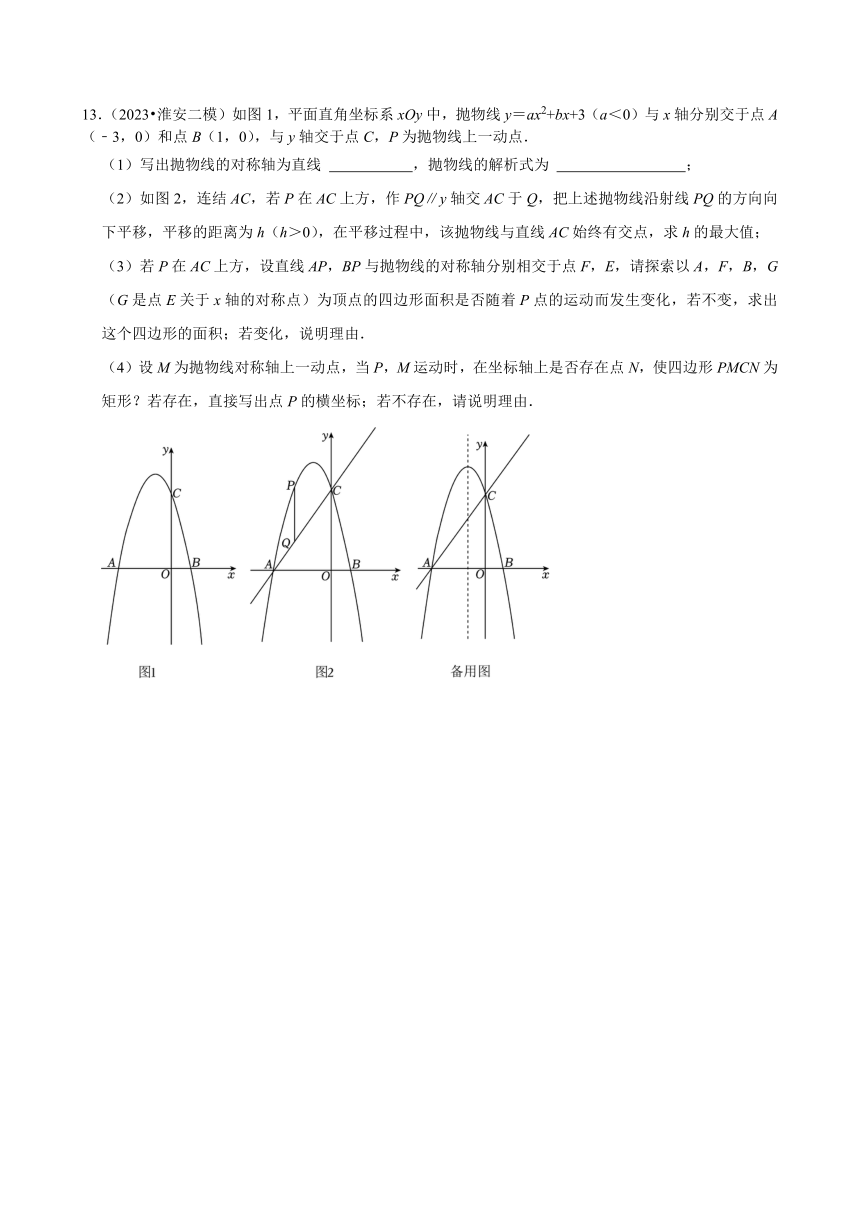
13.(2023 淮安二模)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+3(a<0)与x轴分别交于点A(﹣3,0)和点B(1,0),与y轴交于点C,P为抛物线上一动点.
(1)写出抛物线的对称轴为直线 ,抛物线的解析式为 ;
(2)如图2,连结AC,若P在AC上方,作PQ∥y轴交AC于Q,把上述抛物线沿射线PQ的方向向下平移,平移的距离为h(h>0),在平移过程中,该抛物线与直线AC始终有交点,求h的最大值;
(3)若P在AC上方,设直线AP,BP与抛物线的对称轴分别相交于点F,E,请探索以A,F,B,G(G是点E关于x轴的对称点)为顶点的四边形面积是否随着P点的运动而发生变化,若不变,求出这个四边形的面积;若变化,说明理由.
(4)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P的横坐标;若不存在,请说明理由.
14.(2022 宿迁)从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
15.(2023 仪征市模拟)如图,在△ABC中,AB=AC,以AB为直径作⊙O,⊙O交BC于点D,交CA的延长线于点E.过点D作DF⊥AC,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若AB=4,∠C=30°,求劣弧的长.
16.(2021 鄂尔多斯)如图,矩形ABCD的两边AB,BC的长分别为3,8,C,D在y轴上,E是AD的中点,反比例函数y=(k≠0)的图象经过点E,与BC交于点F,且CF﹣BE=1.
(1)求反比例函数的解析式;
(2)在y轴上找一点P,使得S△CEP=S矩形ABCD,求此时点P的坐标.
17.(2023 淮安区一模)某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.
(1)用含x的代数式表示:每件商品的销售价为 元,每件商品的利润为 元,每周的商品销售量为 件;
(2)求y关于x的函数关系式(不要求写出x的取值范围);
(3)应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
18.(2022 福建)在平面直角坐标系xOy中,已知抛物线y=ax2+bx经过A(4,0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
(1)求抛物线的解析式;
(2)若△OAB面积是△PAB面积的2倍,求点P的坐标;
(3)如图,OP交AB于点C,PD∥BO交AB于点D.记△CDP,△CPB,△CBO的面积分别为S1,S2,S3.判断+是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
参考答案与试题解析
一.选择题(共4小题)
1.【解答】解:∵菱形ABCD的对角线AC,BD的长分别为6和8,
∴AC⊥BD,这个菱形的面积=AC BD=×6×8=24,
故选:C.
2.【解答】解:函数y=kx+b的图象经过点(2,0),并且函数值y随x的增大而减小,
所以当x<2时,函数值大于0,即关于x的不等式kx+b>0的解集是x<2.
故选:A.
3.【解答】解:∵关于x的方程x2﹣x﹣m=0没有实数根,
∴Δ=(﹣1)2﹣4×1×(﹣m)=1+4m<0,
解得:,
故选:A.
4.【解答】解:∵方程的其中一个根是1,
∴3﹣2+m=0,解得m=﹣1,
∵两根的积为,
∴两根的积为﹣,
故选:D.
二.填空题(共5小题)
5.【解答】解:∵x 4=﹣4,
∴x2﹣4x=﹣4,
则(x﹣2)2=0,
解得:x1=x2=2.
故答案为:2.
6.【解答】解:∵点A(2,2)在函数y=(x>0)的图象上,
∴2=,得k=4,
∵在Rt△ABC中,AC∥x轴,AC=2,
∴点B的横坐标是4,
∴y==1,
∴点B的坐标为(4,1),
故答案为:(4,1).
7.【解答】解:∵圆锥的侧面积为25π,底面半径为5,
∴5πl=25π.
解得:l=5,
故答案为:5.
8.【解答】解:∵()2=,()2=,<,
∴<,
故答案为:<.
9.【解答】解:方法一:∵∠BAC=90°,AB=3,BC=5,
∴AC===4,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO=2,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴,
∴,
∴OP′=,
∴则PQ的最小值为2OP′=,
方法二:过点A作AE⊥BC垂足为E 当PQ⊥BC时,符合题意,则四边形AEPQ是矩形,
∴PQ=AE=2.4.
故答案为:.
三.解答题(共9小题)
10.【解答】解:(1)AD为⊙O的切线,
理由:连接OA,并延长交⊙O于点E,连接BE,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠E+∠EAB=90°,
∵∠C=∠E,∠C=∠BAD,
∴∠E=∠BAD,
∴∠EAB+∠BAD=90°,
∴∠EAD=90°,
∴AD为⊙O的切线;
(2)∵BD⊥AB,
∴∠ABD=90°,
∵∠ABE=90°,
∴∠ABE+∠ABD=180°,
∴点E、B、D三点在同一条直线上,
在Rt△ABD中,AD=9,BD=6,
∴AB===3,
∵∠E=∠BAD,∠ABE=∠ABD=90°,
∴△EBA∽△ABD,
∴=,
∴=,
解得:AE=,
∴⊙O半径为.
11.【解答】解:(1)设y与x之间的函数关系式为y=kx+b,
∴,
解得k=﹣10,b=600,
∴y与x之间的函数关系式为y=﹣10x+600,
故答案为:y=﹣10x+600;
(2)设利润为w元,
则w=(x﹣20)y=(x﹣20)(﹣10x+600)=﹣10(x﹣20)(x﹣60)=﹣10(x2﹣80x+1200)=﹣10(x﹣40)2+4000,
∵每天笔筒的销售量不低于210件,
∴﹣10x+600≥210,
解得x≤39,
∵a=﹣10<0,
∴x=39时,w最大=3990,
∴当销售单价为39元时,每天获取的利润最大,最大利润是3990元.
12.【解答】(1)证明:如图1,过点C作CF∥AB,与DE的延长线交于点F,
∵CF∥AB,
∴∠F=∠ADE,∠A=∠ECF,
∵点E是AC的中点,
∴AE=CE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴DE=EF,AD=CF,
∵点D是AB的中点,
∴AD=BD,
∴CF=BD,
又∵CF∥AB,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE=BC,
故答案为:△CFE;平行四边形;
(2)解:如图2,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
∴∠A=∠ADH=90°,
又∵AE=DE,∠AEG=∠DEH,
∴△AEG≌△DEH(ASA),
∴GE=EH,
∵∠GEF=90°,
∴GF=HF,
∴∠A=∠HDE=90°,AG=HD=,
∵∠ADC=120°,
∴∠HDF=360°﹣90°﹣120°=150°,
∴∠HDP=30°,
∴PH=DH=,PD=,
∴PF=PD+DF=+4=,
∴HF===,
∴GF=;
(3)解:如图3,取BC的中点N,连接DN,
∵点D是AC的中点,点N是BC的中点,
∴AD=CD,BN=CN,
∴DN∥AB,AB=2DN,
∵=K,
∴设BG=2a,则CG=2aK,BC=2a+2aK,
∴CN=BN=a+aK,
∴GN=aK﹣a,
∵AB=AC,
∴DC=DN,
∴∠DNC=∠DCN,
∴∠DNG=∠DCE,
∵DG=DE,
∴∠E=∠DGE,
∴△DGN≌△DEC(AAS),
∴GN=CE=aK﹣a,
∴BE=2a+2aK+aK﹣a=3aK+a,NE=2aK,
∴DN∥AB,
∴△DNE∽△FBE,
∴=,
∴设DN=2Kx,BF=(3K+1)x,
∴AB=4Kx,AF=AB﹣BF=(K﹣1)x,
∴=.
13.【解答】解:(1)由题意得,抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),
则﹣3a=3,则a=﹣1,
故抛物线的表达式为:y=﹣x2﹣2x+3,
则抛物线的对称轴为x=﹣1,
故答案为:x=﹣1,y=﹣x2﹣2x+3;
(2)由题意得,平移后的抛物线表达式为:y=﹣x2﹣2x+3﹣h①,
由抛物线的表达式知,点C(0,3),
由点A、C的坐标得,直线AC的表达式为:y=x+3②,
联立①②得:﹣x2﹣2x+3﹣h=x+3,
则Δ=9﹣4h=0,
则h=,
即h的最大值为:;
(3)面积不变,为16,理由:
设点P的坐标为(m,﹣m2﹣2m+3),
由点A、P的坐标得,直线AP的表达式为:y=(1﹣m)(x+3),
当x=﹣1时,y=(1﹣m)(x+3)=2﹣2m,
即点F(﹣1,2﹣2m),
同理可得,点E(﹣1,2m+6),则点G(﹣1,﹣2m﹣6),
则FG=2﹣2m+2m+6=8,
则S四边形AGBF=AB×FG=4×8=16,
即以A,F,B,G(G是点E关于x轴的对称点)为顶点的四边形面积不随着P点的运动而发生变化,这个四边形的面积为16;
(4)存在,理由如下:
如图,当点N在y轴上时,四边形PMCN是矩形,此时P(﹣1,4),N(0,4);
如图,当四边形PMCN是矩形时,设M(﹣1,n),P(t,﹣t2﹣2t+3),则N(t+1,0),
由题意,
消去n得,3t2+5t﹣10=0,
解得t=,
综上所述,满足条件的点P的横坐标为:,﹣1.
14.【解答】解:(1)由题意可得,
甲一定参加比赛,再从其余3名学生中任意选取1名,有3种可能性,其中选中丙的有1种可能性,
故恰好选中丙的概率是,
故答案为:;
(2)树状图如下:
由上可得,一共有12种可能性,其中一定有乙的可能性有6种,
故一定有乙的概率是=.
15.【解答】(1)证明:连接OD,
∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠C=∠ODB,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,
∵∠B=∠C=30°,
∴∠EAB=∠B+∠C=60°,
∴∠EOB=2∠EAB=120°,
∴的长==.
16.【解答】解:(1)∵E是AD的中点,
∴AE=,
在Rt△ABE中,由勾股定理得:BE=,
∵CF﹣BE=1,
∴CF=6,
∴F的横坐标为﹣6,
设F(﹣6,m),则E(﹣4,m+3),
∵E,F都在反比例函数图象上,
∴﹣6m=﹣4(m+3),
解得m=6,
∴F(﹣6,6),
∴k=﹣36,
∴反比例函数y=﹣.
(2)∵S△CEP=S矩形ABCD,
∴,
∴CP=8,
∴P(0,14)或(0,﹣2).
17.【解答】解:(1)每件商品的销售价为:(x+40)元,每件商品的利润为:(x+10)元,
每周的商品销售量为:(180﹣5x)件;
故答案为:x+40,x+10,180﹣5x;
(2)所求函数关系式为:y=(x+10)(180﹣5x)
即y=﹣5x2+130x+1800;
(3)∵在y=﹣5x2+130x+1800中,
a=﹣5<0,b=130,x=1800,
∴当x=﹣=﹣=13时,x+40=13+40=53,
y有最大值且最大值为:=1800﹣=2645(元),
∴当售价为53元时,可获得最大利润2645元.
18.【解答】解:(1)将A(4,0),B(1,4)代入y=ax2+bx,
∴,解得.
∴抛物线的解析式为:y=﹣x2+x.
(2)设直线AB的解析式为:y=kx+t,
将A(4,0),B(1,4)代入y=kx+t,
∴,
解得.
∵A(4,0),B(1,4),
∴S△OAB=×4×4=8,
∴S△OAB=2S△PAB=8,即S△PAB=4,
过点P作PM⊥x轴于点M,PM与AB交于点N,过点B作BE⊥PM于点E,如图,
∴S△PAB=S△PNB+S△PNA=PN×BE+PN×AM=PN=4,
∴PN=.
设点P的横坐标为m,
∴P(m,﹣m2+m)(1<m<4),N(m,﹣m+),
∴PN=﹣m2+m﹣(﹣m+)=.
解得m=2或m=3;
∴P(2,)或(3,4).
(3)∵PD∥OB,
∴∠DPC=∠BOC,∠PDC=∠OBC,
∴△DPC∽△BOC,
∴CP:CO=CD:CB=PD:OB,
∵==,==,
∴+=.
设直线AB交y轴于点F.则F(0,),
过点P作PH⊥x轴,垂足为H,PH交AB于点G,如图,
∵∠PDC=∠OBC,
∴∠PDG=∠OBF,
∵PG∥OF,
∴∠PGD=∠OFB,
∴△PDG∽△OBF,
∴PD:OB=PG:OF,
设P(n,﹣n2+n)(1<n<4),
由(2)可知,PG=﹣n2+n﹣,
∴+===PG=﹣(n﹣)2+.
∵1<n<4,
∴当n=时,+的最大值为.
声明:试题解析著作权
一.选择题(共4小题)
1.(2023 淮安二模)如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的面积是( )
A.48 B.40 C.24 D.20
2.(2022 乌鲁木齐)一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )
A.x<2 B.x<0 C.x>0 D.x>2
3.(2020 攀枝花)若关于x的方程x2﹣x﹣m=0没有实数根,则m的值可以为( )
A.﹣1 B.﹣ C.0 D.1
4.(2022 乐山)关于x的一元二次方程3x2﹣2x+m=0有两根,其中一根为x=1,则这两根之积为( )
A. B. C.1 D.﹣
二.填空题(共5小题)
5.(2024 涟水县模拟)对于实数a、b,定义新运算“ ”:a b=a2﹣ab,如4 2=42﹣4×2=8.若x 4=﹣4,则实数x的值是 .
6.(2021 浙江)如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为 .
7.(2024 涟水县模拟)若圆锥的侧面积为25π,底面半径为5,则该圆锥的母线长是 .
8.(2022 临沂)比较大小: (填“>”,“<”或“=”).
9.(2022 毕节市)如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ长度的最小值为 .
三.解答题(共9小题)
10.(2023 淮安二模)如图,已知AB是⊙O的弦,C为⊙O上一点,∠C=∠BAD.
(1)请判断AD是否为⊙O的切线,并证明你的结论;
(2)若BD⊥AB于点B,AD=9,BD=6,求⊙O半径.
11.(2023 淮安二模)某网店专门销售某种品牌的笔筒,成本为20元/件,每天销售量y(件)与销售单价x(元)之间存在一次函数关系,如图,其中规定每天笔筒的销售量不低于210件.
(1)写出y与x之间的函数关系式 ;
(2)当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
12.(2023 淮安二模)我们知道,三角形的中位线平行于三角形的第三边,并且等于第三边的一半,如何证明三角形中位线定理呢?
(1)【方法回顾】
证明:三角形中位线定理.
已知:如图,在△ABC中,D、E分别是AB、AC的中点.
求证:DE∥BC,.
证明三角形中位线性质定理的方法很多,但多数都需要通过添加辅助线构图去完成,下面是其中一种证法的添加辅助线方法,阅读并完成填空:
添加辅助线,如图1,在△ABC中,过点C作CF∥AB,与DE的延长线交于点F.可证△ADE≌ ,根据全等三角形对应边相等可得DE=EF,然后判断出四边形BCFD是 ,根据图形性质可证得DE∥BC,.
(2)【方法迁移】
如图2,在四边形ABCD中,AD∥BC,∠A=90°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若,DF=4,∠GEF=90°,求GF的长.
(3)【定理应用】
如图3,在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,,延长BC至点E,使DE=DG,延长ED交AB于点F,直接写出的值(用含K的式子表示).
13.(2023 淮安二模)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+3(a<0)与x轴分别交于点A(﹣3,0)和点B(1,0),与y轴交于点C,P为抛物线上一动点.
(1)写出抛物线的对称轴为直线 ,抛物线的解析式为 ;
(2)如图2,连结AC,若P在AC上方,作PQ∥y轴交AC于Q,把上述抛物线沿射线PQ的方向向下平移,平移的距离为h(h>0),在平移过程中,该抛物线与直线AC始终有交点,求h的最大值;
(3)若P在AC上方,设直线AP,BP与抛物线的对称轴分别相交于点F,E,请探索以A,F,B,G(G是点E关于x轴的对称点)为顶点的四边形面积是否随着P点的运动而发生变化,若不变,求出这个四边形的面积;若变化,说明理由.
(4)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P的横坐标;若不存在,请说明理由.
14.(2022 宿迁)从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
15.(2023 仪征市模拟)如图,在△ABC中,AB=AC,以AB为直径作⊙O,⊙O交BC于点D,交CA的延长线于点E.过点D作DF⊥AC,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若AB=4,∠C=30°,求劣弧的长.
16.(2021 鄂尔多斯)如图,矩形ABCD的两边AB,BC的长分别为3,8,C,D在y轴上,E是AD的中点,反比例函数y=(k≠0)的图象经过点E,与BC交于点F,且CF﹣BE=1.
(1)求反比例函数的解析式;
(2)在y轴上找一点P,使得S△CEP=S矩形ABCD,求此时点P的坐标.
17.(2023 淮安区一模)某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.
(1)用含x的代数式表示:每件商品的销售价为 元,每件商品的利润为 元,每周的商品销售量为 件;
(2)求y关于x的函数关系式(不要求写出x的取值范围);
(3)应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
18.(2022 福建)在平面直角坐标系xOy中,已知抛物线y=ax2+bx经过A(4,0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.
(1)求抛物线的解析式;
(2)若△OAB面积是△PAB面积的2倍,求点P的坐标;
(3)如图,OP交AB于点C,PD∥BO交AB于点D.记△CDP,△CPB,△CBO的面积分别为S1,S2,S3.判断+是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
参考答案与试题解析
一.选择题(共4小题)
1.【解答】解:∵菱形ABCD的对角线AC,BD的长分别为6和8,
∴AC⊥BD,这个菱形的面积=AC BD=×6×8=24,
故选:C.
2.【解答】解:函数y=kx+b的图象经过点(2,0),并且函数值y随x的增大而减小,
所以当x<2时,函数值大于0,即关于x的不等式kx+b>0的解集是x<2.
故选:A.
3.【解答】解:∵关于x的方程x2﹣x﹣m=0没有实数根,
∴Δ=(﹣1)2﹣4×1×(﹣m)=1+4m<0,
解得:,
故选:A.
4.【解答】解:∵方程的其中一个根是1,
∴3﹣2+m=0,解得m=﹣1,
∵两根的积为,
∴两根的积为﹣,
故选:D.
二.填空题(共5小题)
5.【解答】解:∵x 4=﹣4,
∴x2﹣4x=﹣4,
则(x﹣2)2=0,
解得:x1=x2=2.
故答案为:2.
6.【解答】解:∵点A(2,2)在函数y=(x>0)的图象上,
∴2=,得k=4,
∵在Rt△ABC中,AC∥x轴,AC=2,
∴点B的横坐标是4,
∴y==1,
∴点B的坐标为(4,1),
故答案为:(4,1).
7.【解答】解:∵圆锥的侧面积为25π,底面半径为5,
∴5πl=25π.
解得:l=5,
故答案为:5.
8.【解答】解:∵()2=,()2=,<,
∴<,
故答案为:<.
9.【解答】解:方法一:∵∠BAC=90°,AB=3,BC=5,
∴AC===4,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO=2,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴,
∴,
∴OP′=,
∴则PQ的最小值为2OP′=,
方法二:过点A作AE⊥BC垂足为E 当PQ⊥BC时,符合题意,则四边形AEPQ是矩形,
∴PQ=AE=2.4.
故答案为:.
三.解答题(共9小题)
10.【解答】解:(1)AD为⊙O的切线,
理由:连接OA,并延长交⊙O于点E,连接BE,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠E+∠EAB=90°,
∵∠C=∠E,∠C=∠BAD,
∴∠E=∠BAD,
∴∠EAB+∠BAD=90°,
∴∠EAD=90°,
∴AD为⊙O的切线;
(2)∵BD⊥AB,
∴∠ABD=90°,
∵∠ABE=90°,
∴∠ABE+∠ABD=180°,
∴点E、B、D三点在同一条直线上,
在Rt△ABD中,AD=9,BD=6,
∴AB===3,
∵∠E=∠BAD,∠ABE=∠ABD=90°,
∴△EBA∽△ABD,
∴=,
∴=,
解得:AE=,
∴⊙O半径为.
11.【解答】解:(1)设y与x之间的函数关系式为y=kx+b,
∴,
解得k=﹣10,b=600,
∴y与x之间的函数关系式为y=﹣10x+600,
故答案为:y=﹣10x+600;
(2)设利润为w元,
则w=(x﹣20)y=(x﹣20)(﹣10x+600)=﹣10(x﹣20)(x﹣60)=﹣10(x2﹣80x+1200)=﹣10(x﹣40)2+4000,
∵每天笔筒的销售量不低于210件,
∴﹣10x+600≥210,
解得x≤39,
∵a=﹣10<0,
∴x=39时,w最大=3990,
∴当销售单价为39元时,每天获取的利润最大,最大利润是3990元.
12.【解答】(1)证明:如图1,过点C作CF∥AB,与DE的延长线交于点F,
∵CF∥AB,
∴∠F=∠ADE,∠A=∠ECF,
∵点E是AC的中点,
∴AE=CE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴DE=EF,AD=CF,
∵点D是AB的中点,
∴AD=BD,
∴CF=BD,
又∵CF∥AB,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE=BC,
故答案为:△CFE;平行四边形;
(2)解:如图2,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
∴∠A=∠ADH=90°,
又∵AE=DE,∠AEG=∠DEH,
∴△AEG≌△DEH(ASA),
∴GE=EH,
∵∠GEF=90°,
∴GF=HF,
∴∠A=∠HDE=90°,AG=HD=,
∵∠ADC=120°,
∴∠HDF=360°﹣90°﹣120°=150°,
∴∠HDP=30°,
∴PH=DH=,PD=,
∴PF=PD+DF=+4=,
∴HF===,
∴GF=;
(3)解:如图3,取BC的中点N,连接DN,
∵点D是AC的中点,点N是BC的中点,
∴AD=CD,BN=CN,
∴DN∥AB,AB=2DN,
∵=K,
∴设BG=2a,则CG=2aK,BC=2a+2aK,
∴CN=BN=a+aK,
∴GN=aK﹣a,
∵AB=AC,
∴DC=DN,
∴∠DNC=∠DCN,
∴∠DNG=∠DCE,
∵DG=DE,
∴∠E=∠DGE,
∴△DGN≌△DEC(AAS),
∴GN=CE=aK﹣a,
∴BE=2a+2aK+aK﹣a=3aK+a,NE=2aK,
∴DN∥AB,
∴△DNE∽△FBE,
∴=,
∴设DN=2Kx,BF=(3K+1)x,
∴AB=4Kx,AF=AB﹣BF=(K﹣1)x,
∴=.
13.【解答】解:(1)由题意得,抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),
则﹣3a=3,则a=﹣1,
故抛物线的表达式为:y=﹣x2﹣2x+3,
则抛物线的对称轴为x=﹣1,
故答案为:x=﹣1,y=﹣x2﹣2x+3;
(2)由题意得,平移后的抛物线表达式为:y=﹣x2﹣2x+3﹣h①,
由抛物线的表达式知,点C(0,3),
由点A、C的坐标得,直线AC的表达式为:y=x+3②,
联立①②得:﹣x2﹣2x+3﹣h=x+3,
则Δ=9﹣4h=0,
则h=,
即h的最大值为:;
(3)面积不变,为16,理由:
设点P的坐标为(m,﹣m2﹣2m+3),
由点A、P的坐标得,直线AP的表达式为:y=(1﹣m)(x+3),
当x=﹣1时,y=(1﹣m)(x+3)=2﹣2m,
即点F(﹣1,2﹣2m),
同理可得,点E(﹣1,2m+6),则点G(﹣1,﹣2m﹣6),
则FG=2﹣2m+2m+6=8,
则S四边形AGBF=AB×FG=4×8=16,
即以A,F,B,G(G是点E关于x轴的对称点)为顶点的四边形面积不随着P点的运动而发生变化,这个四边形的面积为16;
(4)存在,理由如下:
如图,当点N在y轴上时,四边形PMCN是矩形,此时P(﹣1,4),N(0,4);
如图,当四边形PMCN是矩形时,设M(﹣1,n),P(t,﹣t2﹣2t+3),则N(t+1,0),
由题意,
消去n得,3t2+5t﹣10=0,
解得t=,
综上所述,满足条件的点P的横坐标为:,﹣1.
14.【解答】解:(1)由题意可得,
甲一定参加比赛,再从其余3名学生中任意选取1名,有3种可能性,其中选中丙的有1种可能性,
故恰好选中丙的概率是,
故答案为:;
(2)树状图如下:
由上可得,一共有12种可能性,其中一定有乙的可能性有6种,
故一定有乙的概率是=.
15.【解答】(1)证明:连接OD,
∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠C=∠ODB,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,
∵∠B=∠C=30°,
∴∠EAB=∠B+∠C=60°,
∴∠EOB=2∠EAB=120°,
∴的长==.
16.【解答】解:(1)∵E是AD的中点,
∴AE=,
在Rt△ABE中,由勾股定理得:BE=,
∵CF﹣BE=1,
∴CF=6,
∴F的横坐标为﹣6,
设F(﹣6,m),则E(﹣4,m+3),
∵E,F都在反比例函数图象上,
∴﹣6m=﹣4(m+3),
解得m=6,
∴F(﹣6,6),
∴k=﹣36,
∴反比例函数y=﹣.
(2)∵S△CEP=S矩形ABCD,
∴,
∴CP=8,
∴P(0,14)或(0,﹣2).
17.【解答】解:(1)每件商品的销售价为:(x+40)元,每件商品的利润为:(x+10)元,
每周的商品销售量为:(180﹣5x)件;
故答案为:x+40,x+10,180﹣5x;
(2)所求函数关系式为:y=(x+10)(180﹣5x)
即y=﹣5x2+130x+1800;
(3)∵在y=﹣5x2+130x+1800中,
a=﹣5<0,b=130,x=1800,
∴当x=﹣=﹣=13时,x+40=13+40=53,
y有最大值且最大值为:=1800﹣=2645(元),
∴当售价为53元时,可获得最大利润2645元.
18.【解答】解:(1)将A(4,0),B(1,4)代入y=ax2+bx,
∴,解得.
∴抛物线的解析式为:y=﹣x2+x.
(2)设直线AB的解析式为:y=kx+t,
将A(4,0),B(1,4)代入y=kx+t,
∴,
解得.
∵A(4,0),B(1,4),
∴S△OAB=×4×4=8,
∴S△OAB=2S△PAB=8,即S△PAB=4,
过点P作PM⊥x轴于点M,PM与AB交于点N,过点B作BE⊥PM于点E,如图,
∴S△PAB=S△PNB+S△PNA=PN×BE+PN×AM=PN=4,
∴PN=.
设点P的横坐标为m,
∴P(m,﹣m2+m)(1<m<4),N(m,﹣m+),
∴PN=﹣m2+m﹣(﹣m+)=.
解得m=2或m=3;
∴P(2,)或(3,4).
(3)∵PD∥OB,
∴∠DPC=∠BOC,∠PDC=∠OBC,
∴△DPC∽△BOC,
∴CP:CO=CD:CB=PD:OB,
∵==,==,
∴+=.
设直线AB交y轴于点F.则F(0,),
过点P作PH⊥x轴,垂足为H,PH交AB于点G,如图,
∵∠PDC=∠OBC,
∴∠PDG=∠OBF,
∵PG∥OF,
∴∠PGD=∠OFB,
∴△PDG∽△OBF,
∴PD:OB=PG:OF,
设P(n,﹣n2+n)(1<n<4),
由(2)可知,PG=﹣n2+n﹣,
∴+===PG=﹣(n﹣)2+.
∵1<n<4,
∴当n=时,+的最大值为.
声明:试题解析著作权
同课章节目录
