圆柱与圆锥应用题(专项训练)2023-2024学年数学六年级下册人教版(含解析)
文档属性
| 名称 | 圆柱与圆锥应用题(专项训练)2023-2024学年数学六年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 567.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 08:27:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆柱与圆锥应用题(专项训练)2023-2024学年数学六年级下册人教版
典例分析一 .学校组织手工比赛,丹丹制作了一个形状如下图所示的茶叶罐。为装饰茶叶罐,她在罐的表面上画上喜欢的画(底面也要绘画),需要绘画的面积是多少平方厘米? 【答案】408.2平方厘米 【分析】 根据题意,结合圆柱的表面积公式:,代入数据计算即可。 【详解】 3.14×10×8+3.14××2 =31.4×8+3.14××2 =251.2+3.14×25×2 =251.2+78.5×2 =251.2+157 =408.2(平方厘米) 答:需要绘画的面积是408.2平方厘米。 典例分析二 .小军想测量一个瓶子的容积,测得瓶子的底面内直径是6厘米,往瓶子内装入一些水,正放时水面高10厘米,如果将它倒置放平,空瓶部分的高度是6厘米。瓶子的容积是多少毫升? 【答案】452.16毫升 【分析】瓶子的容积相当于底面直径为6厘米,高为厘米的圆柱体的体积,根据圆柱体积,将数值代入计算即可。 【详解】 = = =452.16(立方厘米) =452.16(毫升) 答:瓶子的容积是452.16毫升。 【点睛】 典例分析三 .唐老鸭用一个圆锥形容器装满了香油,共2000毫升,米老鼠趁唐老鸭不在,在容器侧面的正中间咬了一个洞,然后开始偷油,一直偷到油面与洞口平齐为止(如图,此时油面直径是圆锥形容器底面直径的一半)。米老鼠一共偷了多少毫升的香油?(容器的厚度不计) 【答案】1750毫升 【分析】 将圆锥形容器的容积,即原来香油的体积看作单位“1”,假设大圆锥的底面半径为2r,则小圆锥的底面半径为r,同样设大圆锥的高为2h,则小圆锥的高为h,根据圆锥体积=底面积×高÷3,分别用字母表示出圆锥形容器的容积和剩余香油的体积,剩余香油的体积÷圆锥形容器的容积=剩余香油体积是原来香油体积的几分之几,原来香油的体积×剩余香油体积的对应分率=剩余香油的体积,原来香油的体积-剩余香油的体积=米老鼠偷的香油体积,据此列式解答。 【详解】 假设大圆锥的底面半径为2r,则小圆锥的底面半径为r,大圆锥的高为2h,则小圆锥的高为h。 大圆锥体积: 小圆锥体积: 2000-2000× =2000-250 =1750(毫升) 答:米老鼠一共偷了1750毫升的香油。 【点睛】 关键是掌握并灵活运用圆锥体积公式,确定剩余香油和原来香油的体积之间的关系。
跟踪训练
1.一个圆柱形蓄水池地面直径是20米,深3米,在周围和底部抹上水泥,每平方米需要水泥23千克,共需要多少千克水泥?
2.学校把一个堆成底面直径是2米,高6米的圆锥形沙子,填铺到一个长8米,宽3.14米的沙坑里,可以铺多厚?
3.一个圆锥形沙堆,底面直径2米,高1.5米。如果用容积是0.3立方米的小车来运,需要几次可以运完?
4.妈妈想给小雨的水壶做一个布套(如图),准备10平方分米的布料够吗?
5.一个长方体水箱,从里面量长是12.56厘米,宽是10厘米。把一个底面半径为4厘米,高12厘米的圆锥形铅锤浸没在水中,水面会上升多少厘米?
6.把一块长是20厘米,宽是10厘米,高是9.42厘米的长方体铁块熔铸成一个底面半径是10厘米的圆柱形铁块。这个圆柱形铁块的高是多少厘米?
7.把一根长2.4米,底面直径是0.6米的圆柱形钢材平均截成4段,表面积增加了多少平方米?
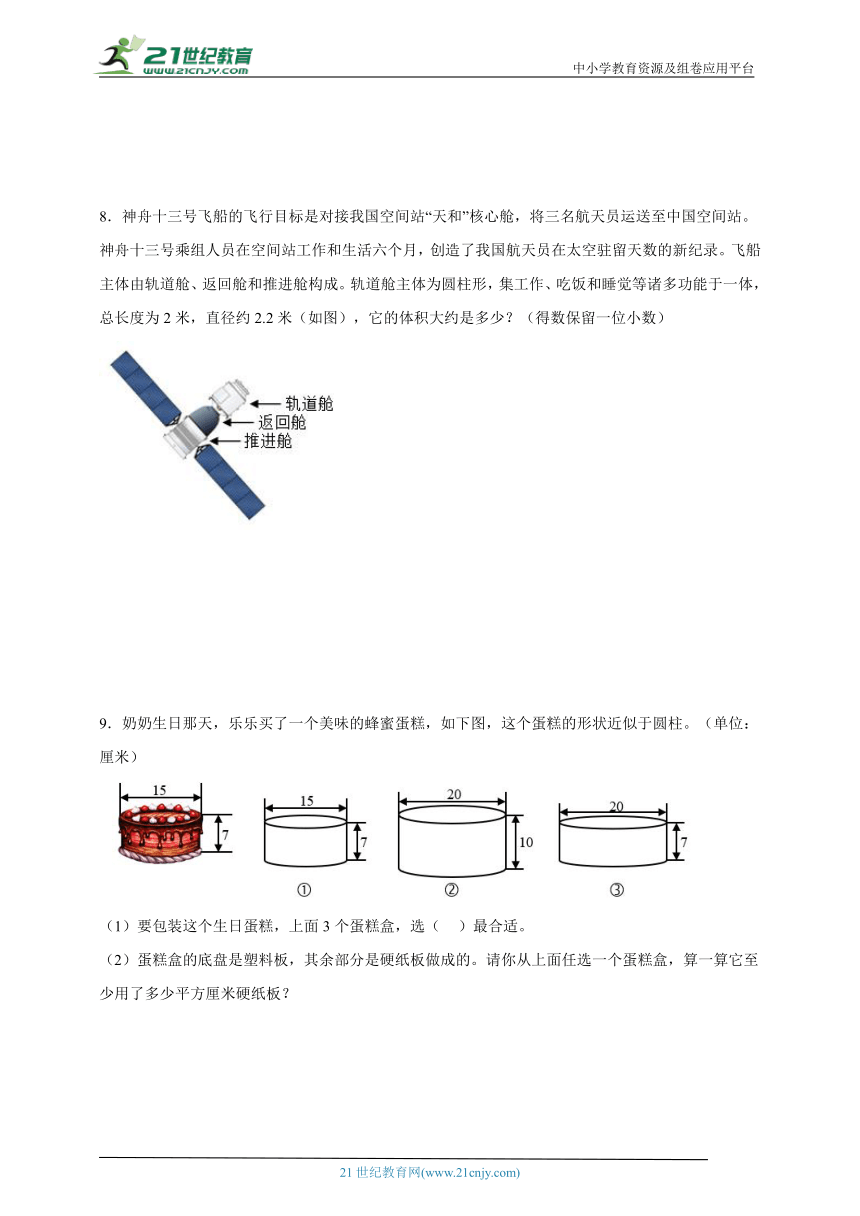
8.神舟十三号飞船的飞行目标是对接我国空间站“天和”核心舱,将三名航天员运送至中国空间站。神舟十三号乘组人员在空间站工作和生活六个月,创造了我国航天员在太空驻留天数的新纪录。飞船主体由轨道舱、返回舱和推进舱构成。轨道舱主体为圆柱形,集工作、吃饭和睡觉等诸多功能于一体,总长度为2米,直径约2.2米(如图),它的体积大约是多少?(得数保留一位小数)
9.奶奶生日那天,乐乐买了一个美味的蜂蜜蛋糕,如下图,这个蛋糕的形状近似于圆柱。(单位:厘米)
(1)要包装这个生日蛋糕,上面3个蛋糕盒,选( )最合适。
(2)蛋糕盒的底盘是塑料板,其余部分是硬纸板做成的。请你从上面任选一个蛋糕盒,算一算它至少用了多少平方厘米硬纸板?
10.如图一个蒙古包由一个圆柱和一个圆锥组成。
(1)这个蒙古包的占地面积是多少平方米?
(2)这个蒙古包所占的空间是多少立方米?
11.下面这个长方形的长是10厘米,宽是2厘米,分别以长和宽为轴旋转一周,得到两个圆柱体。
①以宽为轴旋转一周后得到的圆柱的占地面积是多少平方厘米?
②以长为轴旋转一周后得到的圆柱的体积是多少立方厘米?
12.妈妈怕杯子烫手,在杯子中部套上了一个用毛线勾出的装饰品,这个装饰品的面积是多少平方厘米?如果把0.5升的水倒入杯中,能不能正好装满?(杯子的厚度忽略不计)
13.如图,长方体容器内装有一些纯果汁,容器的底面是边长为8厘米正方形。圆锥容器里装满水,现将水与纯果汁按一定比混合,调成一杯果汁倒入圆柱形玻璃杯内,果汁占杯子的。原长方体容器内纯果汁的高度是多少?(①取3;②不考虑所有容器的厚度)
14.一个装满水的矿泉水瓶,内直径是8厘米。小明喝了一些,水的高度还有6厘米,把瓶盖拧紧后倒置放平,无水部分高10厘米。小明喝了多少水?
15.一个圆锥的底面半径是3分米。从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥表面积增加了24平方分米。这个圆锥的体积是多少立方分米?
参考答案:
1.11555.2千克
【分析】根据题意,在圆柱形蓄水池的周围和底部抹上水泥,那么抹水泥的面积=圆柱的侧面积+圆柱下底的面积,根据S侧=πdh,S底=πr2,代入数据计算,求出抹水泥的面积,再乘每平方米需用到的水泥质量,即是一共需要的水泥质量。
【详解】3.14×20×3+3.14×(20÷2)2
=3.14×60+3.14×100
=188.4+314
=502.4(平方米)
502.4×23=11555.2(千克)
答:共需要11555.2千克水泥。
【点睛】本题考查圆柱的表面积公式的灵活运用,弄清少了哪个面,要求的是哪些面的面积之和,再利用公式列式计算。
2.0.25米
【分析】根据圆锥的体积公式:V=Sh,据此求出沙子的体积,沙子的体积不变,再根据长方体的体积公式:V=abh,据此解答即可。
【详解】×3.14×(2÷2)2×6÷8÷3.14
=×3.14×1×6÷8÷3.14
=6.28÷8÷3.14
=0.785÷3.14
=0.25(米)
答:可以铺0.25米。
【点睛】本题考查圆锥和长方体的体积,熟记公式是解题的关键。
3.6次
【分析】根据“”求出沙堆的体积,需要运送的次数=沙堆的体积÷小车的容积,余下的沙子装不满一车时需要多运送一次,结果用进一法取整数。
【详解】×(2÷2)2×1.5×3.14
=×1×1.5×3.14
=0.5×3.14
=1.57(立方米)
1.57÷0.3≈6(次)
答:需要6次可以运完。
【点睛】掌握圆锥的体积计算公式和商取近似数的方法是解答题目的关键。
4.够
【分析】根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式求出这个圆柱的表面积,然后与10平方分米进行比较即可。
【详解】3.14×10×20+3.14×(10÷2)2×2
=31.4×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(平方厘米)
10平方分米=1000平方厘米
785平方厘米<1000平方厘米
答:准备10平方分米的布料够。
【点睛】此题的解题关键是灵活运用圆柱的表面积公式解决实际的问题。
5.1.6厘米
【分析】根据“长方形的面积=长×宽”求出长方体水箱的底面积,再利用“”求出铅锤的体积,水面上升的高度=铅锤的体积÷长方体水箱的底面积。
【详解】×12×42×3.14÷(12.56×10)
=×12×42×3.14÷125.6
=4×42×3.14÷125.6
=64×3.14÷125.6
=200.96÷125.6
=1.6(厘米)
答:水面会上升1.6厘米。
【点睛】掌握长方体和圆锥的体积计算公式是解答题目的关键。
6.6厘米
【分析】先求出长方体铁块的体积,由于熔铸前后铁块的体积不变,所以用铁块体积除以圆柱的底面积,即可求出圆柱形铁块的高度。
【详解】20×10×9.42÷(3.14×102)
=1884÷314
=6(厘米)
答:这个圆柱形铁块的高是6厘米。
【点睛】本题考查了圆柱和长方体的体积,圆柱的体积=底面积×高,长方体的体积=长×宽×高。
7.1.6956平方米
【分析】根据题意,把一根圆柱形钢材平均截成4段,要截3次,每截一次增加2个面,共增加6个截面的面积;截面是圆柱的底面积,根据公式S=πr2,求出一个截面的面积,再乘6即是增加的表面积。
【详解】增加的面:
(4-1)×2
=3×2
=6(个)
增加的表面积:
3.14×(0.6÷2)2×6
=3.14×0.09×6
=0.2826×6
=1.6956(平方米)
答:表面积增加了1.6956平方米。
【点睛】本题考查圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,求出圆柱的底面积是解题的关键。
8.7.6立方米
【分析】根据圆柱的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(2.2÷2)2×2
=3.14×1.12×2
=3.7994×2
≈7.6(立方米)
答:它的体积大约是7.6立方米。
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
9.(1)②
(2)942平方厘米
【分析】(1)蛋糕的形状近似于圆柱,底面直径是15厘米,高是7厘米,所选蛋糕盒的尺寸应该在直径和高的长度上都大于蛋糕的尺寸,才能装下蛋糕又留有一定的空间,据此可以选择②号蛋糕盒;
(2)可以选择②号蛋糕盒来计算。因为底盘是塑料板,其余部分是硬纸板,所以,硬纸板的面积就等于一个底面积与侧面积的和;列综合算式为:3.14×(20÷2)2+3.14×20×10。
【详解】(1)要包装这个生日蛋糕,选择(②)最合适;
(2)3.14×(20÷2)2+3.14×20×10
=3.14×100+3.14×200
=314+628
=942(平方厘米)
答:②号蛋糕盒,至少用了942平方厘米的硬纸板。
【点睛】懂的结合日常生活现象选择蛋糕盒;明确蛋糕盒硬纸板的面积是由哪几部分组成的,是解题关键。
10.(1)28.26平方米
(2)65.94立方米
【分析】(1)这个蒙古包的占地面是一个圆形,根据圆的面积公式即可求出它的占地面积;
(2)根据圆柱和圆锥的体积公式,分别求出这个蒙古包上下两部分的体积,再相加求出它的总体积。
【详解】(1)3.14×(6÷2)2
=3.14×9
=28.26(平方米)
答:这个蒙古包的占地面积是28.26平方米。
(2)28.26×2+×28.26×(3-2)
=56.52+×28.26×1
=56.52+9.42
=65.94(立方米)
答:这个蒙古包所占的空间是65.94立方米。
【点睛】本题考查了圆柱和圆锥的体积。圆柱体积=底面积×高,圆锥体积=×底面积×高。
11.①314平方厘米
②125.6立方厘米
【分析】①以宽为轴旋转一周后得到的圆柱的底面半径是10厘米,根据圆的面积公式:S=πr2,据此求出占地面积即可;
②以长为轴旋转一周后得到的圆柱的底面半径是2厘米,高是10厘米,根据圆柱的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】①3.14×102=314(平方厘米)
答:以宽为轴旋转一周后得到的圆柱的占地面积是314平方厘米。
②3.14×22×10
=3.14×4×10
=12.56×10
=125.6(立方厘米)
答:以长为轴旋转一周后得到的圆柱的体积是125.6立方厘米。
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
12.125.6平方厘米;不能
【分析】求装饰品的面积,可根据圆柱的侧面积公式:S=,d=8厘米,h=5厘米,代入即可求出这个装饰品的面积;根据圆柱的体积(容积)公式:V=,求出这个杯子的容积,换算单位后,与0.5升比较大小,即可得解。
【详解】3.14×8×5=125.6(平方厘米)
3.14×(8÷2)2×15
=3.14×42×15
=3.14×16×15
=753.6(立方厘米)
753.6立方厘米=0.7536升
0.7536>0.5,所以装不满。
答:这个装饰品的面积是125.6平方厘米,如果把0.5升的水倒入杯中,不能装满。
【点睛】此题的解题关键是灵活运用圆柱的侧面积和体积(容积)公式,解决实际的问题。
13.3.75厘米
【分析】根据圆锥体积=底面积×高÷3,圆柱体积=底面积×高,分别求出圆锥和圆柱容器的容积,将圆柱容器的容积看作单位“1”,圆柱容器容积×=果汁体积,果汁体积-水的体积=纯果汁体积,再根据长方体的高=体积÷底面积,即可求出原长方体容器内纯果汁的高度。
【详解】3×(8÷2)2×15÷3
=3×16×5
=240(立方厘米)
3×(8÷2)2×15
=3×16×15
=720(立方厘米)
720×=480(立方厘米)
(480-240)÷(8×8)
=240÷64
=3.75(厘米)
答:原长方体容器内纯果汁的高度是3.75厘米。
【点睛】关键是掌握并灵活运用圆柱、圆锥和长方体体积公式。
14.502.4毫升
【分析】求喝了多少水就是求第二个瓶子空白部分的容积即可,也就是高为10厘米的圆柱的体积,利用圆柱体积公式即可解答。
【详解】3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
答:小明喝了502.4毫升的水。
【点睛】解答本题的关键是理解空白圆柱的体积就是小明喝掉的水的体积。
15.37.68立方分米
【分析】通过观察图形可知,把这个圆锥纵向切开,表面积增加的是两个切面的面积,每个切面的底等于圆锥的底面直径,每个切面的高等于圆锥的高,根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出圆锥的高,再根据圆锥的体积公式:V=,把数据代入公式解答。
【详解】24÷2=12(平方分米)
12×2÷(3×2)
=24÷6
=4(分米)
×3.14×32×4
=×3.14×9×4
=37.68(立方分米)
答:这个圆锥的体积是37.68立方分米。
【点睛】此题主要考查三角形的面积公式、圆锥的体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆柱与圆锥应用题(专项训练)2023-2024学年数学六年级下册人教版
典例分析一 .学校组织手工比赛,丹丹制作了一个形状如下图所示的茶叶罐。为装饰茶叶罐,她在罐的表面上画上喜欢的画(底面也要绘画),需要绘画的面积是多少平方厘米? 【答案】408.2平方厘米 【分析】 根据题意,结合圆柱的表面积公式:,代入数据计算即可。 【详解】 3.14×10×8+3.14××2 =31.4×8+3.14××2 =251.2+3.14×25×2 =251.2+78.5×2 =251.2+157 =408.2(平方厘米) 答:需要绘画的面积是408.2平方厘米。 典例分析二 .小军想测量一个瓶子的容积,测得瓶子的底面内直径是6厘米,往瓶子内装入一些水,正放时水面高10厘米,如果将它倒置放平,空瓶部分的高度是6厘米。瓶子的容积是多少毫升? 【答案】452.16毫升 【分析】瓶子的容积相当于底面直径为6厘米,高为厘米的圆柱体的体积,根据圆柱体积,将数值代入计算即可。 【详解】 = = =452.16(立方厘米) =452.16(毫升) 答:瓶子的容积是452.16毫升。 【点睛】 典例分析三 .唐老鸭用一个圆锥形容器装满了香油,共2000毫升,米老鼠趁唐老鸭不在,在容器侧面的正中间咬了一个洞,然后开始偷油,一直偷到油面与洞口平齐为止(如图,此时油面直径是圆锥形容器底面直径的一半)。米老鼠一共偷了多少毫升的香油?(容器的厚度不计) 【答案】1750毫升 【分析】 将圆锥形容器的容积,即原来香油的体积看作单位“1”,假设大圆锥的底面半径为2r,则小圆锥的底面半径为r,同样设大圆锥的高为2h,则小圆锥的高为h,根据圆锥体积=底面积×高÷3,分别用字母表示出圆锥形容器的容积和剩余香油的体积,剩余香油的体积÷圆锥形容器的容积=剩余香油体积是原来香油体积的几分之几,原来香油的体积×剩余香油体积的对应分率=剩余香油的体积,原来香油的体积-剩余香油的体积=米老鼠偷的香油体积,据此列式解答。 【详解】 假设大圆锥的底面半径为2r,则小圆锥的底面半径为r,大圆锥的高为2h,则小圆锥的高为h。 大圆锥体积: 小圆锥体积: 2000-2000× =2000-250 =1750(毫升) 答:米老鼠一共偷了1750毫升的香油。 【点睛】 关键是掌握并灵活运用圆锥体积公式,确定剩余香油和原来香油的体积之间的关系。
跟踪训练
1.一个圆柱形蓄水池地面直径是20米,深3米,在周围和底部抹上水泥,每平方米需要水泥23千克,共需要多少千克水泥?
2.学校把一个堆成底面直径是2米,高6米的圆锥形沙子,填铺到一个长8米,宽3.14米的沙坑里,可以铺多厚?
3.一个圆锥形沙堆,底面直径2米,高1.5米。如果用容积是0.3立方米的小车来运,需要几次可以运完?
4.妈妈想给小雨的水壶做一个布套(如图),准备10平方分米的布料够吗?
5.一个长方体水箱,从里面量长是12.56厘米,宽是10厘米。把一个底面半径为4厘米,高12厘米的圆锥形铅锤浸没在水中,水面会上升多少厘米?
6.把一块长是20厘米,宽是10厘米,高是9.42厘米的长方体铁块熔铸成一个底面半径是10厘米的圆柱形铁块。这个圆柱形铁块的高是多少厘米?
7.把一根长2.4米,底面直径是0.6米的圆柱形钢材平均截成4段,表面积增加了多少平方米?
8.神舟十三号飞船的飞行目标是对接我国空间站“天和”核心舱,将三名航天员运送至中国空间站。神舟十三号乘组人员在空间站工作和生活六个月,创造了我国航天员在太空驻留天数的新纪录。飞船主体由轨道舱、返回舱和推进舱构成。轨道舱主体为圆柱形,集工作、吃饭和睡觉等诸多功能于一体,总长度为2米,直径约2.2米(如图),它的体积大约是多少?(得数保留一位小数)
9.奶奶生日那天,乐乐买了一个美味的蜂蜜蛋糕,如下图,这个蛋糕的形状近似于圆柱。(单位:厘米)
(1)要包装这个生日蛋糕,上面3个蛋糕盒,选( )最合适。
(2)蛋糕盒的底盘是塑料板,其余部分是硬纸板做成的。请你从上面任选一个蛋糕盒,算一算它至少用了多少平方厘米硬纸板?
10.如图一个蒙古包由一个圆柱和一个圆锥组成。
(1)这个蒙古包的占地面积是多少平方米?
(2)这个蒙古包所占的空间是多少立方米?
11.下面这个长方形的长是10厘米,宽是2厘米,分别以长和宽为轴旋转一周,得到两个圆柱体。
①以宽为轴旋转一周后得到的圆柱的占地面积是多少平方厘米?
②以长为轴旋转一周后得到的圆柱的体积是多少立方厘米?
12.妈妈怕杯子烫手,在杯子中部套上了一个用毛线勾出的装饰品,这个装饰品的面积是多少平方厘米?如果把0.5升的水倒入杯中,能不能正好装满?(杯子的厚度忽略不计)
13.如图,长方体容器内装有一些纯果汁,容器的底面是边长为8厘米正方形。圆锥容器里装满水,现将水与纯果汁按一定比混合,调成一杯果汁倒入圆柱形玻璃杯内,果汁占杯子的。原长方体容器内纯果汁的高度是多少?(①取3;②不考虑所有容器的厚度)
14.一个装满水的矿泉水瓶,内直径是8厘米。小明喝了一些,水的高度还有6厘米,把瓶盖拧紧后倒置放平,无水部分高10厘米。小明喝了多少水?
15.一个圆锥的底面半径是3分米。从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥表面积增加了24平方分米。这个圆锥的体积是多少立方分米?
参考答案:
1.11555.2千克
【分析】根据题意,在圆柱形蓄水池的周围和底部抹上水泥,那么抹水泥的面积=圆柱的侧面积+圆柱下底的面积,根据S侧=πdh,S底=πr2,代入数据计算,求出抹水泥的面积,再乘每平方米需用到的水泥质量,即是一共需要的水泥质量。
【详解】3.14×20×3+3.14×(20÷2)2
=3.14×60+3.14×100
=188.4+314
=502.4(平方米)
502.4×23=11555.2(千克)
答:共需要11555.2千克水泥。
【点睛】本题考查圆柱的表面积公式的灵活运用,弄清少了哪个面,要求的是哪些面的面积之和,再利用公式列式计算。
2.0.25米
【分析】根据圆锥的体积公式:V=Sh,据此求出沙子的体积,沙子的体积不变,再根据长方体的体积公式:V=abh,据此解答即可。
【详解】×3.14×(2÷2)2×6÷8÷3.14
=×3.14×1×6÷8÷3.14
=6.28÷8÷3.14
=0.785÷3.14
=0.25(米)
答:可以铺0.25米。
【点睛】本题考查圆锥和长方体的体积,熟记公式是解题的关键。
3.6次
【分析】根据“”求出沙堆的体积,需要运送的次数=沙堆的体积÷小车的容积,余下的沙子装不满一车时需要多运送一次,结果用进一法取整数。
【详解】×(2÷2)2×1.5×3.14
=×1×1.5×3.14
=0.5×3.14
=1.57(立方米)
1.57÷0.3≈6(次)
答:需要6次可以运完。
【点睛】掌握圆锥的体积计算公式和商取近似数的方法是解答题目的关键。
4.够
【分析】根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式求出这个圆柱的表面积,然后与10平方分米进行比较即可。
【详解】3.14×10×20+3.14×(10÷2)2×2
=31.4×20+3.14×52×2
=628+3.14×25×2
=628+157
=785(平方厘米)
10平方分米=1000平方厘米
785平方厘米<1000平方厘米
答:准备10平方分米的布料够。
【点睛】此题的解题关键是灵活运用圆柱的表面积公式解决实际的问题。
5.1.6厘米
【分析】根据“长方形的面积=长×宽”求出长方体水箱的底面积,再利用“”求出铅锤的体积,水面上升的高度=铅锤的体积÷长方体水箱的底面积。
【详解】×12×42×3.14÷(12.56×10)
=×12×42×3.14÷125.6
=4×42×3.14÷125.6
=64×3.14÷125.6
=200.96÷125.6
=1.6(厘米)
答:水面会上升1.6厘米。
【点睛】掌握长方体和圆锥的体积计算公式是解答题目的关键。
6.6厘米
【分析】先求出长方体铁块的体积,由于熔铸前后铁块的体积不变,所以用铁块体积除以圆柱的底面积,即可求出圆柱形铁块的高度。
【详解】20×10×9.42÷(3.14×102)
=1884÷314
=6(厘米)
答:这个圆柱形铁块的高是6厘米。
【点睛】本题考查了圆柱和长方体的体积,圆柱的体积=底面积×高,长方体的体积=长×宽×高。
7.1.6956平方米
【分析】根据题意,把一根圆柱形钢材平均截成4段,要截3次,每截一次增加2个面,共增加6个截面的面积;截面是圆柱的底面积,根据公式S=πr2,求出一个截面的面积,再乘6即是增加的表面积。
【详解】增加的面:
(4-1)×2
=3×2
=6(个)
增加的表面积:
3.14×(0.6÷2)2×6
=3.14×0.09×6
=0.2826×6
=1.6956(平方米)
答:表面积增加了1.6956平方米。
【点睛】本题考查圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,求出圆柱的底面积是解题的关键。
8.7.6立方米
【分析】根据圆柱的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(2.2÷2)2×2
=3.14×1.12×2
=3.7994×2
≈7.6(立方米)
答:它的体积大约是7.6立方米。
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
9.(1)②
(2)942平方厘米
【分析】(1)蛋糕的形状近似于圆柱,底面直径是15厘米,高是7厘米,所选蛋糕盒的尺寸应该在直径和高的长度上都大于蛋糕的尺寸,才能装下蛋糕又留有一定的空间,据此可以选择②号蛋糕盒;
(2)可以选择②号蛋糕盒来计算。因为底盘是塑料板,其余部分是硬纸板,所以,硬纸板的面积就等于一个底面积与侧面积的和;列综合算式为:3.14×(20÷2)2+3.14×20×10。
【详解】(1)要包装这个生日蛋糕,选择(②)最合适;
(2)3.14×(20÷2)2+3.14×20×10
=3.14×100+3.14×200
=314+628
=942(平方厘米)
答:②号蛋糕盒,至少用了942平方厘米的硬纸板。
【点睛】懂的结合日常生活现象选择蛋糕盒;明确蛋糕盒硬纸板的面积是由哪几部分组成的,是解题关键。
10.(1)28.26平方米
(2)65.94立方米
【分析】(1)这个蒙古包的占地面是一个圆形,根据圆的面积公式即可求出它的占地面积;
(2)根据圆柱和圆锥的体积公式,分别求出这个蒙古包上下两部分的体积,再相加求出它的总体积。
【详解】(1)3.14×(6÷2)2
=3.14×9
=28.26(平方米)
答:这个蒙古包的占地面积是28.26平方米。
(2)28.26×2+×28.26×(3-2)
=56.52+×28.26×1
=56.52+9.42
=65.94(立方米)
答:这个蒙古包所占的空间是65.94立方米。
【点睛】本题考查了圆柱和圆锥的体积。圆柱体积=底面积×高,圆锥体积=×底面积×高。
11.①314平方厘米
②125.6立方厘米
【分析】①以宽为轴旋转一周后得到的圆柱的底面半径是10厘米,根据圆的面积公式:S=πr2,据此求出占地面积即可;
②以长为轴旋转一周后得到的圆柱的底面半径是2厘米,高是10厘米,根据圆柱的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】①3.14×102=314(平方厘米)
答:以宽为轴旋转一周后得到的圆柱的占地面积是314平方厘米。
②3.14×22×10
=3.14×4×10
=12.56×10
=125.6(立方厘米)
答:以长为轴旋转一周后得到的圆柱的体积是125.6立方厘米。
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
12.125.6平方厘米;不能
【分析】求装饰品的面积,可根据圆柱的侧面积公式:S=,d=8厘米,h=5厘米,代入即可求出这个装饰品的面积;根据圆柱的体积(容积)公式:V=,求出这个杯子的容积,换算单位后,与0.5升比较大小,即可得解。
【详解】3.14×8×5=125.6(平方厘米)
3.14×(8÷2)2×15
=3.14×42×15
=3.14×16×15
=753.6(立方厘米)
753.6立方厘米=0.7536升
0.7536>0.5,所以装不满。
答:这个装饰品的面积是125.6平方厘米,如果把0.5升的水倒入杯中,不能装满。
【点睛】此题的解题关键是灵活运用圆柱的侧面积和体积(容积)公式,解决实际的问题。
13.3.75厘米
【分析】根据圆锥体积=底面积×高÷3,圆柱体积=底面积×高,分别求出圆锥和圆柱容器的容积,将圆柱容器的容积看作单位“1”,圆柱容器容积×=果汁体积,果汁体积-水的体积=纯果汁体积,再根据长方体的高=体积÷底面积,即可求出原长方体容器内纯果汁的高度。
【详解】3×(8÷2)2×15÷3
=3×16×5
=240(立方厘米)
3×(8÷2)2×15
=3×16×15
=720(立方厘米)
720×=480(立方厘米)
(480-240)÷(8×8)
=240÷64
=3.75(厘米)
答:原长方体容器内纯果汁的高度是3.75厘米。
【点睛】关键是掌握并灵活运用圆柱、圆锥和长方体体积公式。
14.502.4毫升
【分析】求喝了多少水就是求第二个瓶子空白部分的容积即可,也就是高为10厘米的圆柱的体积,利用圆柱体积公式即可解答。
【详解】3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
答:小明喝了502.4毫升的水。
【点睛】解答本题的关键是理解空白圆柱的体积就是小明喝掉的水的体积。
15.37.68立方分米
【分析】通过观察图形可知,把这个圆锥纵向切开,表面积增加的是两个切面的面积,每个切面的底等于圆锥的底面直径,每个切面的高等于圆锥的高,根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出圆锥的高,再根据圆锥的体积公式:V=,把数据代入公式解答。
【详解】24÷2=12(平方分米)
12×2÷(3×2)
=24÷6
=4(分米)
×3.14×32×4
=×3.14×9×4
=37.68(立方分米)
答:这个圆锥的体积是37.68立方分米。
【点睛】此题主要考查三角形的面积公式、圆锥的体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
