2023-2024学年数学人教版九年级上册21.2.1 解一元二次方程(1)——直接开方法 课件(共16张PPT)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册21.2.1 解一元二次方程(1)——直接开方法 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 352.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 09:57:31 | ||
图片预览






文档简介
(共16张PPT)
第2课时 解一元二次方程(1)——直接开方法
第二十一章 一元二次方程
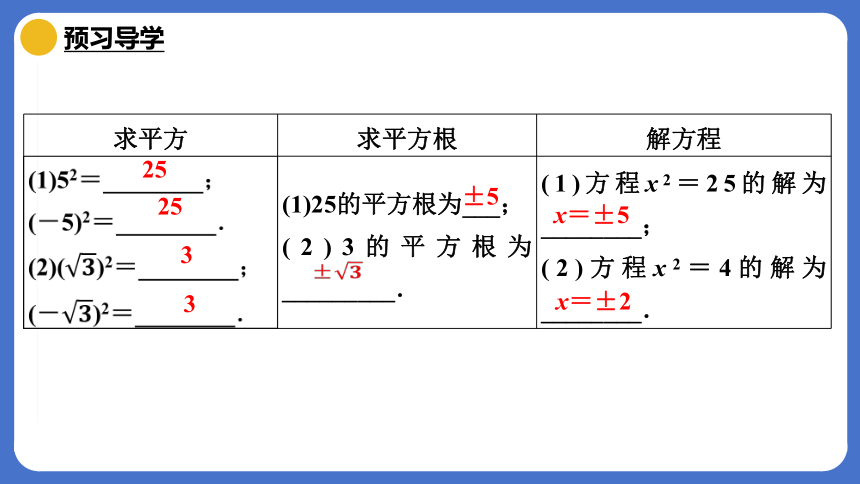
求平方 求平方根 解方程
(1)52=________; (-5)2=________. (2)()2=________; (-)2=________. (1)25的平方根为___; (2)3的平方根为_________. (1)方程x2=25的解为________;
(2)方程x2=4的解为________.
25
25
3
3
±5
±
x=±5
x=±2
【例1】用直接开方法解一元二次方程:
(1)x2=9; (2)x2=3; (3)x2=.
知识点1
解形如x2=p(p≥0)的一元二次方程
解:x=±3.
解:x=±.
解:x=±.
【变式1】用直接开方法解一元二次方程:
(1)x2=25; (2)x2=; (3)x2-20=0.
解:x=±5.
解:x=±.
解:x2=20,
x=±2.
【例2】用直接开方法解一元二次方程:
(1)4x2=9; (2)2x2-8=0; (3)x2=12.
知识点2
解形如ax2=p的一元二次方程
解:x=±.
解:2x2=8,
x2=4,
x=±2.
解:x2=18,
x=±3.
【变式2】用直接开方法解一元二次方程:
(1)4x2=81; (2)36x2-1=0; (3)(易错)9x2+5=1.
解:x2=,
x=±.
解:x2=,
x=±.
解:9x2=-4,
∴方程无实数根.
【例3】用直接开方法解一元二次方程:
(1)2(x+1)2=200; (2)(2x-1)2-64=0.
知识点3
解形如(ax+b)2=p的一元二次方程
解:(x+1)2=100,
x+1=±10,
∴x1=9,x2=-11.
解:(2x-1)2=64,
2x-1=±8,
∴x1=,x2=-.
【变式3】用直接开方法解一元二次方程:
(1)(人教教材母题)(x+6)2-9=0;
解:(x+6)2=9,
x+6=±3,
∴x1=-3,x2=-9.
【变式3】用直接开方法解一元二次方程:
(2)(人教教材母题)3(x-1)2-6=0.
解:3(x-1)2=6,
(x-1)2=2,
x-1=±,
∴x1=1+,x2=1-.
课堂总结:用直接开方法解一元二次方程,要把方程化为x2=p或(ax+b)2=p的形式.
(1)当p>0时,根据平方根的意义,方程有两个不等的实数根x1=________,x2=;
(2)当p=0时,方程有两个相等的实数根x1=x2=0;
(3)当p________0时,因为对任意实数x,都有x2≥0,所以方程无实数根.
-
<
1.(多维原创)若方程(x-1)2=a有实数解,则a的取值范围是( )
A.a≤0 B.a≥0
C.a>0 D.a<0
2.已知1是一元二次方程x2+p=0的一个根,则该方程的另一个根是________.
B
-1
3.解下列方程:
(1)(2x-1)2-8=0;
解:(2x-1)2=16,
2x-1=±4,
∴x1=,x2=-.
3.解下列方程:
(2)(人教教材母题)(x-4)2=(5-2x)2.
解:x-4=±(5-2x),
x-4=5-2x,或x-4=-5+2x,
∴x1=3,x2=1.
4.若(a2+b2-3)2=16,则a2+b2=________.(提示:把a2+b2看作一个整体)
7
5.(应用意识)(人教教材母题)一桶油漆可刷的面积为1 500 dm2,李林用这桶油漆恰好刷完10个如图所示的同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
解:设其中一个盒子的棱长是x dm.
根据题意,得10×6x2=1 500,
解得x=5(负数舍去).
答:盒子的棱长是5 dm.
第2课时 解一元二次方程(1)——直接开方法
第二十一章 一元二次方程
求平方 求平方根 解方程
(1)52=________; (-5)2=________. (2)()2=________; (-)2=________. (1)25的平方根为___; (2)3的平方根为_________. (1)方程x2=25的解为________;
(2)方程x2=4的解为________.
25
25
3
3
±5
±
x=±5
x=±2
【例1】用直接开方法解一元二次方程:
(1)x2=9; (2)x2=3; (3)x2=.
知识点1
解形如x2=p(p≥0)的一元二次方程
解:x=±3.
解:x=±.
解:x=±.
【变式1】用直接开方法解一元二次方程:
(1)x2=25; (2)x2=; (3)x2-20=0.
解:x=±5.
解:x=±.
解:x2=20,
x=±2.
【例2】用直接开方法解一元二次方程:
(1)4x2=9; (2)2x2-8=0; (3)x2=12.
知识点2
解形如ax2=p的一元二次方程
解:x=±.
解:2x2=8,
x2=4,
x=±2.
解:x2=18,
x=±3.
【变式2】用直接开方法解一元二次方程:
(1)4x2=81; (2)36x2-1=0; (3)(易错)9x2+5=1.
解:x2=,
x=±.
解:x2=,
x=±.
解:9x2=-4,
∴方程无实数根.
【例3】用直接开方法解一元二次方程:
(1)2(x+1)2=200; (2)(2x-1)2-64=0.
知识点3
解形如(ax+b)2=p的一元二次方程
解:(x+1)2=100,
x+1=±10,
∴x1=9,x2=-11.
解:(2x-1)2=64,
2x-1=±8,
∴x1=,x2=-.
【变式3】用直接开方法解一元二次方程:
(1)(人教教材母题)(x+6)2-9=0;
解:(x+6)2=9,
x+6=±3,
∴x1=-3,x2=-9.
【变式3】用直接开方法解一元二次方程:
(2)(人教教材母题)3(x-1)2-6=0.
解:3(x-1)2=6,
(x-1)2=2,
x-1=±,
∴x1=1+,x2=1-.
课堂总结:用直接开方法解一元二次方程,要把方程化为x2=p或(ax+b)2=p的形式.
(1)当p>0时,根据平方根的意义,方程有两个不等的实数根x1=________,x2=;
(2)当p=0时,方程有两个相等的实数根x1=x2=0;
(3)当p________0时,因为对任意实数x,都有x2≥0,所以方程无实数根.
-
<
1.(多维原创)若方程(x-1)2=a有实数解,则a的取值范围是( )
A.a≤0 B.a≥0
C.a>0 D.a<0
2.已知1是一元二次方程x2+p=0的一个根,则该方程的另一个根是________.
B
-1
3.解下列方程:
(1)(2x-1)2-8=0;
解:(2x-1)2=16,
2x-1=±4,
∴x1=,x2=-.
3.解下列方程:
(2)(人教教材母题)(x-4)2=(5-2x)2.
解:x-4=±(5-2x),
x-4=5-2x,或x-4=-5+2x,
∴x1=3,x2=1.
4.若(a2+b2-3)2=16,则a2+b2=________.(提示:把a2+b2看作一个整体)
7
5.(应用意识)(人教教材母题)一桶油漆可刷的面积为1 500 dm2,李林用这桶油漆恰好刷完10个如图所示的同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
解:设其中一个盒子的棱长是x dm.
根据题意,得10×6x2=1 500,
解得x=5(负数舍去).
答:盒子的棱长是5 dm.
同课章节目录
