2023-2024学年数学人教版九年级上册21.2.4 第二课时 一元二次方程的根与系数的关系 课件 (共16张PPT)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册21.2.4 第二课时 一元二次方程的根与系数的关系 课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 286.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 10:01:20 | ||
图片预览






文档简介
(共16张PPT)
一元二次方程的根与系数的关系
第二十一章 一元二次方程
根与系数的关系:
一元二次方程ax2+bx+c=0(a≠0)的两个根为x1=,x2=,请计算x1+x2与x1x2.结论:x1+x2=________=________.(前提条件:Δ≥0)
-
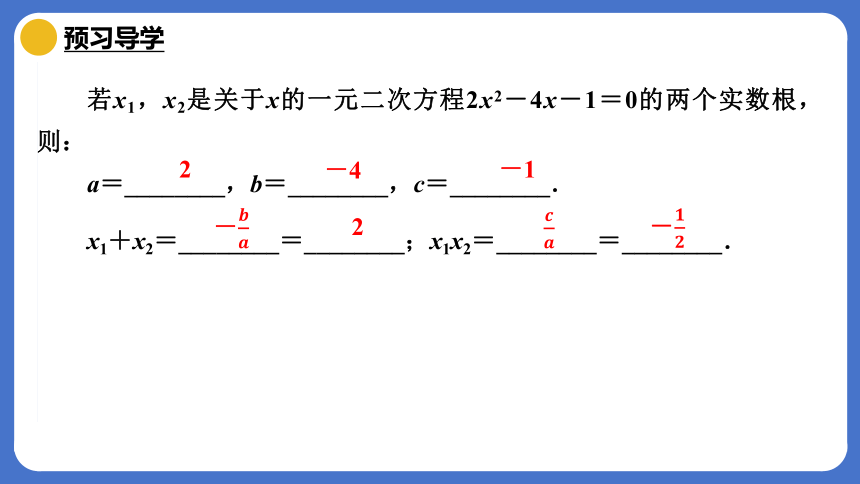
若x1,x2是关于x的一元二次方程2x2-4x-1=0的两个实数根,则:
a=________,b=________,c=________.
x1+x2=________=________;x1x2=________=________.
2
-4
-1
-
2
-
【例1】求下列方程两个根的和与积:
(1)(人教教材母题)3x2+2=1-4x;
知识点1
利用x1+x2=-,x1x2=求两根和与两根积
解:(1)方程化为3x2+4x+1=0.
∴x1+x2=-,x1x2=.
【例1】求下列方程两个根的和与积:
(2)(人教教材母题)7x2-5=x+8.
解:(2)方程化为7x2-x-13=0.
∴x1+x2=,x1x2=-.
【变式1】(1)若方程x2+3x-1=0的两根分别为x1,x2,则x1+x2-x1x2=________.
(2)若矩形的长和宽分别是方程3x2-12x+10=0的两个根,则该矩
形的周长为________,面积为________.
-2
8
【例2】已知方程2x2-4x-3=0的两个根分别为x1,x2,求下列代数式的值.
; (2).
知识点2
利用根与系数的关系求代数式的值
解:∵x1,x2是方程2x2-4x-3=0的两个根,
∴x1+x2=2,x1x2=-.
=(x1+x2)2-2x1x2=22-2×=7.
(2)====-.
【变式2】已知方程x2+3x-2=0的两个根分别为x1,x2,求下列代数式的值.
(1)(x1-x2)2; (2)(x1+3)(x2+3).
解:∵x1,x2是方程x2+3x-2=0的两个根,
∴x1+x2=-3,x1x2=-2.
(1)(x1-x2)2=(x1+x2)2-4x1x2=17.
(2)(x1+3)(x2+3)=x1x2+3(x1+x2)+9=-2.
【例3】已知关于x的一元二次方程x2-4x+m+1=0有两个不相等的实数根.
(1)求m的取值范围;
知识点3
一元二次方程的根与系数的关系和根的判别式的综合
解:(1)∵关于x的一元二次方程x2-4x+m+1=0有两个不相等的实数根,
∴Δ=(-4)2-4(m+1)=16-4m-4>0,
解得m<3.
【例3】已知关于x的一元二次方程x2-4x+m+1=0有两个不相等的实数根.
(2)若该方程的两个实数根x1,x2满足x1+x2=2x1x2,求m的值.
(2)∵该方程的两个实数根为x1,x2,
∴x1+x2=4,x1x2=m+1.
∵x1+x2=2x1x2,
∴2(m+1)=4,解得m=1.
【变式3】已知关于x的一元二次方程x2+(2k+1)x+k2-1=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
解:(1)∵关于x的一元二次方程x2+(2k+1)x+k2-1=0有两个不相等的实数根,
∴(2k+1)2-4(k2-1)>0,
整理,得4k+5>0,
解得k>-.
【变式3】已知关于x的一元二次方程x2+(2k+1)x+k2-1=0有两个不相等的实数根x1,x2.
(2)当x1x2=3时,求k的值.
(2)∵方程的两个根分别为x1,x2,
∴x1x2=k2-1=3,
解得k1=2,k2=-2.
∵k>-,
∴k=2.
1.(多维原创)已知关于x的一元二次方程x2+2x-1=0有两个实数根x1,x2,则下列等式正确的是 ( )
A.x1+x2=2 B.x1x2=-2
C.x1=x2 =6
2.已知α,β满足α+β=3,且αβ=2,写出一个以α,β为两根的一元二次方程:__________________________.
3.已知一元二次方程x2-4x-c=0的一个根为2+,则另一个根为________,c=________.
D
x2-3x+2=0(答案不唯一)
2-
-1
4.(中考新动向)已知关于x的一元二次方程x2+3x+k-2=0有实数根.
(1)求实数k的取值范围;
解:(1)∵关于x的一元二次方程x2+3x+k-2=0有实数根,
∴Δ=32-4×1×(k-2)≥0,
解得k≤.
即k的取值范围是k≤.
4.(中考新动向)已知关于x的一元二次方程x2+3x+k-2=0有实数根.
(2)设方程的两个实数根分别为x1,x2,若(x1+1)(x2+1)=-1,求k的值.
(2)∵方程x2+3x+k-2=0的两个实数根分别为x1,x2,
∴x1+x2=-3,x1x2=k-2.
∵(x1+1)(x2+1)=-1,
∴x1x2+(x1+x2)+1=-1.
∴k-2+(-3)+1=-1,
解得k=3,即k的值是3.
一元二次方程的根与系数的关系
第二十一章 一元二次方程
根与系数的关系:
一元二次方程ax2+bx+c=0(a≠0)的两个根为x1=,x2=,请计算x1+x2与x1x2.结论:x1+x2=________=________.(前提条件:Δ≥0)
-
若x1,x2是关于x的一元二次方程2x2-4x-1=0的两个实数根,则:
a=________,b=________,c=________.
x1+x2=________=________;x1x2=________=________.
2
-4
-1
-
2
-
【例1】求下列方程两个根的和与积:
(1)(人教教材母题)3x2+2=1-4x;
知识点1
利用x1+x2=-,x1x2=求两根和与两根积
解:(1)方程化为3x2+4x+1=0.
∴x1+x2=-,x1x2=.
【例1】求下列方程两个根的和与积:
(2)(人教教材母题)7x2-5=x+8.
解:(2)方程化为7x2-x-13=0.
∴x1+x2=,x1x2=-.
【变式1】(1)若方程x2+3x-1=0的两根分别为x1,x2,则x1+x2-x1x2=________.
(2)若矩形的长和宽分别是方程3x2-12x+10=0的两个根,则该矩
形的周长为________,面积为________.
-2
8
【例2】已知方程2x2-4x-3=0的两个根分别为x1,x2,求下列代数式的值.
; (2).
知识点2
利用根与系数的关系求代数式的值
解:∵x1,x2是方程2x2-4x-3=0的两个根,
∴x1+x2=2,x1x2=-.
=(x1+x2)2-2x1x2=22-2×=7.
(2)====-.
【变式2】已知方程x2+3x-2=0的两个根分别为x1,x2,求下列代数式的值.
(1)(x1-x2)2; (2)(x1+3)(x2+3).
解:∵x1,x2是方程x2+3x-2=0的两个根,
∴x1+x2=-3,x1x2=-2.
(1)(x1-x2)2=(x1+x2)2-4x1x2=17.
(2)(x1+3)(x2+3)=x1x2+3(x1+x2)+9=-2.
【例3】已知关于x的一元二次方程x2-4x+m+1=0有两个不相等的实数根.
(1)求m的取值范围;
知识点3
一元二次方程的根与系数的关系和根的判别式的综合
解:(1)∵关于x的一元二次方程x2-4x+m+1=0有两个不相等的实数根,
∴Δ=(-4)2-4(m+1)=16-4m-4>0,
解得m<3.
【例3】已知关于x的一元二次方程x2-4x+m+1=0有两个不相等的实数根.
(2)若该方程的两个实数根x1,x2满足x1+x2=2x1x2,求m的值.
(2)∵该方程的两个实数根为x1,x2,
∴x1+x2=4,x1x2=m+1.
∵x1+x2=2x1x2,
∴2(m+1)=4,解得m=1.
【变式3】已知关于x的一元二次方程x2+(2k+1)x+k2-1=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
解:(1)∵关于x的一元二次方程x2+(2k+1)x+k2-1=0有两个不相等的实数根,
∴(2k+1)2-4(k2-1)>0,
整理,得4k+5>0,
解得k>-.
【变式3】已知关于x的一元二次方程x2+(2k+1)x+k2-1=0有两个不相等的实数根x1,x2.
(2)当x1x2=3时,求k的值.
(2)∵方程的两个根分别为x1,x2,
∴x1x2=k2-1=3,
解得k1=2,k2=-2.
∵k>-,
∴k=2.
1.(多维原创)已知关于x的一元二次方程x2+2x-1=0有两个实数根x1,x2,则下列等式正确的是 ( )
A.x1+x2=2 B.x1x2=-2
C.x1=x2 =6
2.已知α,β满足α+β=3,且αβ=2,写出一个以α,β为两根的一元二次方程:__________________________.
3.已知一元二次方程x2-4x-c=0的一个根为2+,则另一个根为________,c=________.
D
x2-3x+2=0(答案不唯一)
2-
-1
4.(中考新动向)已知关于x的一元二次方程x2+3x+k-2=0有实数根.
(1)求实数k的取值范围;
解:(1)∵关于x的一元二次方程x2+3x+k-2=0有实数根,
∴Δ=32-4×1×(k-2)≥0,
解得k≤.
即k的取值范围是k≤.
4.(中考新动向)已知关于x的一元二次方程x2+3x+k-2=0有实数根.
(2)设方程的两个实数根分别为x1,x2,若(x1+1)(x2+1)=-1,求k的值.
(2)∵方程x2+3x+k-2=0的两个实数根分别为x1,x2,
∴x1+x2=-3,x1x2=k-2.
∵(x1+1)(x2+1)=-1,
∴x1x2+(x1+x2)+1=-1.
∴k-2+(-3)+1=-1,
解得k=3,即k的值是3.
同课章节目录
