数学:2.3《双曲线及其标准方程》课件(新人教版b选修1-1)
文档属性
| 名称 | 数学:2.3《双曲线及其标准方程》课件(新人教版b选修1-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 405.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 09:03:00 | ||
图片预览






文档简介
课件16张PPT。2019/3/13 双曲线及其
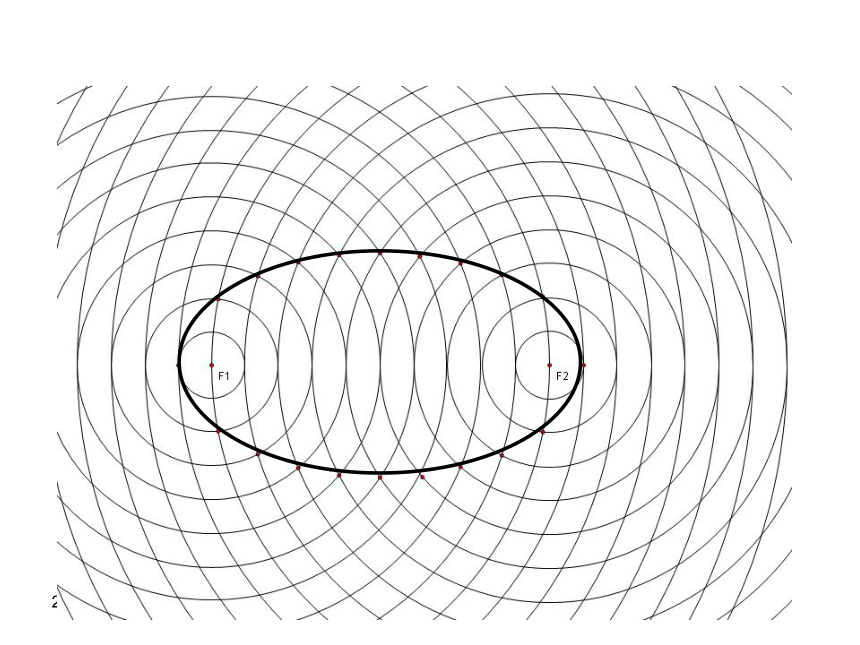
标准方程2019/3/13复习回顾 平面内,动点p到两个定点F1F2的距离和是常数,p形成的轨迹?无轨迹. 轨迹为线段 轨迹为椭圆 2019/3/13平面内,动点p到两个定点F1,F2的距离差是常数2a时,动点p 形成的轨迹?探究2019/3/13在两组同心圆的交点中描出“与F1,F2两点的距离的和等于12”的交点,并用平滑的曲线连成椭圆。2019/3/132019/3/13在两组同心圆的交点中描出“与F1,F2两点的距离的差等于8”的交点。2019/3/13在两组同心圆的交点中描出“与F2,F1两点的距离的差等于8”的交点。2019/3/13在两组同心圆的交点中描出“与F1,F2两点的距离的差的绝对值等于8”的交点,并用平滑的曲线连起来。2019/3/13定义:平面内与两定点F1,F2的距离的差的绝对值等于常数2a 点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距。
2019/3/132019/3/13探究双曲线的标准方程?2019/3/13解:如图建立直角坐标系,则F1(-c,0),F2(c,0).设M(x,y)是双曲线上任意一点,则:||MF1|-|MF2||=2a.①②2019/3/13想一想2019/3/13谁正谁对应 2019/3/13例1、求双曲线的标准方程
(1)已知双曲线的焦点为F1(-5,0)和F2(5,0),双曲线上的点P到F1与F2的距离之差的绝对值为6,求双曲线的标准方程。(变题) (2)已知双曲线的焦点为F1(0,-6)和F2(0,6), 且经过点(2,-5)。2019/3/13知识小结作业双曲线的
标准方程注意1、定义:|MF1|-|MF2|=±2a
2、c>a>0; c2=a2+b2
3、焦点坐标
标准方程2019/3/13复习回顾 平面内,动点p到两个定点F1F2的距离和是常数,p形成的轨迹?无轨迹. 轨迹为线段 轨迹为椭圆 2019/3/13平面内,动点p到两个定点F1,F2的距离差是常数2a时,动点p 形成的轨迹?探究2019/3/13在两组同心圆的交点中描出“与F1,F2两点的距离的和等于12”的交点,并用平滑的曲线连成椭圆。2019/3/132019/3/13在两组同心圆的交点中描出“与F1,F2两点的距离的差等于8”的交点。2019/3/13在两组同心圆的交点中描出“与F2,F1两点的距离的差等于8”的交点。2019/3/13在两组同心圆的交点中描出“与F1,F2两点的距离的差的绝对值等于8”的交点,并用平滑的曲线连起来。2019/3/13定义:平面内与两定点F1,F2的距离的差的绝对值等于常数2a 点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距。
2019/3/132019/3/13探究双曲线的标准方程?2019/3/13解:如图建立直角坐标系,则F1(-c,0),F2(c,0).设M(x,y)是双曲线上任意一点,则:||MF1|-|MF2||=2a.①②2019/3/13想一想2019/3/13谁正谁对应 2019/3/13例1、求双曲线的标准方程
(1)已知双曲线的焦点为F1(-5,0)和F2(5,0),双曲线上的点P到F1与F2的距离之差的绝对值为6,求双曲线的标准方程。(变题) (2)已知双曲线的焦点为F1(0,-6)和F2(0,6), 且经过点(2,-5)。2019/3/13知识小结作业双曲线的
标准方程注意1、定义:|MF1|-|MF2|=±2a
2、c>a>0; c2=a2+b2
3、焦点坐标
