数学:3.2.1《直线的点斜式方程》课件(新人教版a必修2)
文档属性
| 名称 | 数学:3.2.1《直线的点斜式方程》课件(新人教版a必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 85.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 09:04:00 | ||
图片预览






文档简介
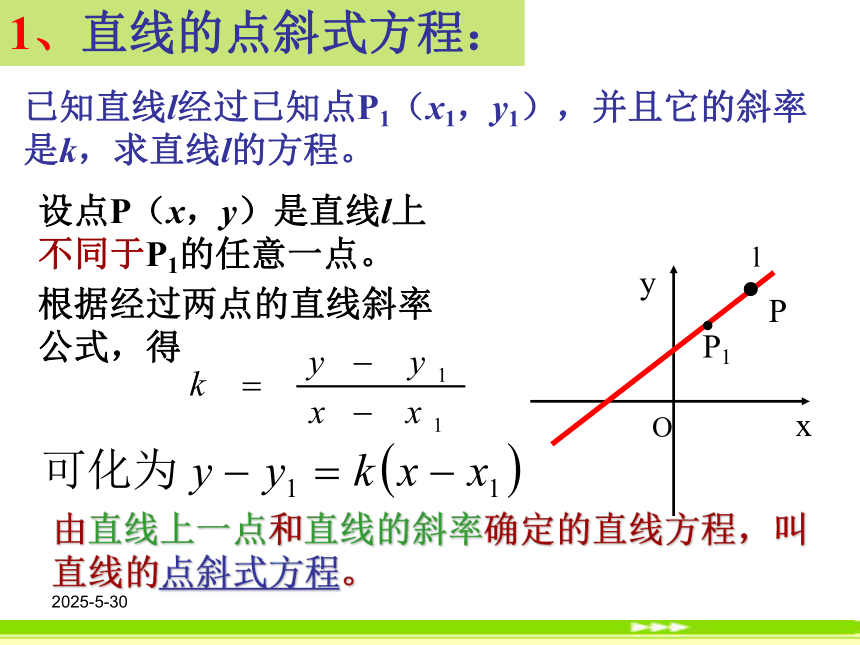
课件17张PPT。2019/3/13复习回顾两条直线平行与垂直的判定条件:不重合、都有斜率条件:都有斜率2019/3/13 如果以一个方程的解为坐标的点都上某条直线上的点,反过来,这条直线上的点的坐标都是这个方程的解,那么,这个方程就叫做这条直线的方程,这条直线就叫做这个方程的直线.直线方程的概念新课讲授2019/3/13已知直线l经过已知点P1(x1,y1),并且它的斜率是k,求直线l的方程。l根据经过两点的直线斜率
公式,得由直线上一点和直线的斜率确定的直线方程,叫直线的点斜式方程。1、直线的点斜式方程:设点P(x,y)是直线l上不同于P1的任意一点。2019/3/131、直线的点斜式方程:(1)、当直线l的倾斜角是00时,tan00=0,即k=0,这时直线l与x轴平行或重合l的方程:y-y1=0 或 y=y1(2)、当直线l的倾斜角是900时,直线l没有斜率,这时直线l与y轴平行或重合l的方程:x-x1=0 或 x=x12019/3/13点斜式方程的应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2Oxy-55°P1°°2019/3/131、写出下列直线的点斜式方程:练习2019/3/132、直线的斜截式方程:已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程。代入点斜式方程,得l的直线方程:
y - b =k ( x - 0)即 y = k x + b 。(2) 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距。 方程(2)是由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。2019/3/13斜截式方程的应用:例2:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4斜截式方程:y = k x + b 几何意义:k 是直线的斜率,b是直线在y轴上的截距2019/3/13练习3、写出下列直线的斜截式方程:2019/3/13练习4、已知直线l过A(3,-5)和B(-2,5),求直线l的方程解:∵直线l过点A(3,-5)和B(-2,5)将A(3,-5),k=-2代入点斜式,得y-(-5) =-2 ( x-3 )
即 2x + y -1 = 02019/3/13例题分析:∥∥2019/3/13练习判断下列各直线是否平行或垂直
(1)
(2)2019/3/13①直线的点斜式,斜截式方程在直线斜率存在时才可以应用。
②直线方程的最后形式应表示成二元一次方程的一般形式。总结:2019/3/13练习5、求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程。解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1直线过点(1,2)代入点斜式方程得y- 2 = x - 1 或y-2=-(x-1)即x-y+1=0或x+y-1=02019/3/13练习㈢巩固:
①经过点(- ,2)倾斜角是300的直线的方程是
(A)y+ = ( x-2) (B)y+2= (x- )
(C)y-2= (x+ )(D)y-2= (x+ )
②已知直线方程y-3= (x-4),则这条直线经过的已知
点,倾斜角分别是
(A)(4,3);π/ 3 (B)(-3,-4);π/ 6
(C)(4,3);π/ 6 (D)(-4,-3);π/ 3
③直线方程可表示成点斜式方程的条件是
(A)直线的斜率存在 (B)直线的斜率不存在
(C)直线不过原点 (D)不同于上述答案
2019/3/13 已知A(0,3),B(-1,0),C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列)。2019/3/13注意:直线上任意一点P与这条直线上一个定点P1所确定的斜率都相等。⑵ 当P点与P1重合时,有x=x1,y=y1,此时满足y-y1=k(x-x1),所以直线l上所有点的坐标都满足y-y1=k(x-x1),而不在直线l上的点,显然不满足(y-y1)/(x-x1)=k即不满足y-y1=k(x-x1),因此y-y1=k(x-x1)是直线l的方程。⑶ 如直线l过P1且平行于x轴,则它的斜率k=0,由点斜式 知方程为y=y0;如果直线l过P1且平行于Y轴,此时它的倾斜角是900,而它的斜率不存在,它的方程不能用点斜式表示,但这时直线上任一点的横坐标x都等于P1的横坐标所以方程为x=x1⑴ P为直线上的任意一点,它的位置与方程无关Oxy°P1°°°°°°°P°°°°°°
公式,得由直线上一点和直线的斜率确定的直线方程,叫直线的点斜式方程。1、直线的点斜式方程:设点P(x,y)是直线l上不同于P1的任意一点。2019/3/131、直线的点斜式方程:(1)、当直线l的倾斜角是00时,tan00=0,即k=0,这时直线l与x轴平行或重合l的方程:y-y1=0 或 y=y1(2)、当直线l的倾斜角是900时,直线l没有斜率,这时直线l与y轴平行或重合l的方程:x-x1=0 或 x=x12019/3/13点斜式方程的应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2Oxy-55°P1°°2019/3/131、写出下列直线的点斜式方程:练习2019/3/132、直线的斜截式方程:已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程。代入点斜式方程,得l的直线方程:
y - b =k ( x - 0)即 y = k x + b 。(2) 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距。 方程(2)是由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。2019/3/13斜截式方程的应用:例2:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4斜截式方程:y = k x + b 几何意义:k 是直线的斜率,b是直线在y轴上的截距2019/3/13练习3、写出下列直线的斜截式方程:2019/3/13练习4、已知直线l过A(3,-5)和B(-2,5),求直线l的方程解:∵直线l过点A(3,-5)和B(-2,5)将A(3,-5),k=-2代入点斜式,得y-(-5) =-2 ( x-3 )
即 2x + y -1 = 02019/3/13例题分析:∥∥2019/3/13练习判断下列各直线是否平行或垂直
(1)
(2)2019/3/13①直线的点斜式,斜截式方程在直线斜率存在时才可以应用。
②直线方程的最后形式应表示成二元一次方程的一般形式。总结:2019/3/13练习5、求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程。解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1直线过点(1,2)代入点斜式方程得y- 2 = x - 1 或y-2=-(x-1)即x-y+1=0或x+y-1=02019/3/13练习㈢巩固:
①经过点(- ,2)倾斜角是300的直线的方程是
(A)y+ = ( x-2) (B)y+2= (x- )
(C)y-2= (x+ )(D)y-2= (x+ )
②已知直线方程y-3= (x-4),则这条直线经过的已知
点,倾斜角分别是
(A)(4,3);π/ 3 (B)(-3,-4);π/ 6
(C)(4,3);π/ 6 (D)(-4,-3);π/ 3
③直线方程可表示成点斜式方程的条件是
(A)直线的斜率存在 (B)直线的斜率不存在
(C)直线不过原点 (D)不同于上述答案
2019/3/13 已知A(0,3),B(-1,0),C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列)。2019/3/13注意:直线上任意一点P与这条直线上一个定点P1所确定的斜率都相等。⑵ 当P点与P1重合时,有x=x1,y=y1,此时满足y-y1=k(x-x1),所以直线l上所有点的坐标都满足y-y1=k(x-x1),而不在直线l上的点,显然不满足(y-y1)/(x-x1)=k即不满足y-y1=k(x-x1),因此y-y1=k(x-x1)是直线l的方程。⑶ 如直线l过P1且平行于x轴,则它的斜率k=0,由点斜式 知方程为y=y0;如果直线l过P1且平行于Y轴,此时它的倾斜角是900,而它的斜率不存在,它的方程不能用点斜式表示,但这时直线上任一点的横坐标x都等于P1的横坐标所以方程为x=x1⑴ P为直线上的任意一点,它的位置与方程无关Oxy°P1°°°°°°°P°°°°°°
