第九章 统计 章末检测试题(含解析)
文档属性
| 名称 | 第九章 统计 章末检测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 371.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第九章 统计 章末检测试题(含解析)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.本试卷共19小题,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题 共58分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某单位有职工160人,其中业务员104人,管理人员32人,后勤服务人员24人,现用比例分配的分层随机抽样法从中抽取一容量为20的样本,则抽取管理人员有( )
A.3人 B.4人 C.7人 D.12人
2.某社团有60人,下表为此社团的年龄频数分布表,则此社团第60百分位数为( )
年龄/岁 36 38 39 43 46 48 50 55 58 60 62 65
频数 4 5 7 5 5 2 1 10 7 8 3 3
A.50 B.49 C.55 D.58
3.为了解我国13岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60 m;从南方抽取了200个男孩,平均身高1.50 m,由此可推断我国13岁的男孩平均身高为( )
A.1.54 m B.1.55 m C.1.56 m D.1.57 m
4.某班有50名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名学生的成绩统计有误,学生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )
A.70和67 B.70和50 C.75和50 D.75和67
5.某居民小区年龄在岁到岁的居民共有人,
如图是他们上网情况的频率分布直方图,现已知年龄
在的人数分别是、人,则年龄
在的频数( )
A.30 B.9
C.6 D.45
年龄(岁) 12 13 14 15
人数(个) 2 4 6 8
6.统计学校排球队员的年龄,发现有12、13、14、15等四
种年龄,统计结果如下表:
根据表中信息可以判断该排球队员年龄的
平均数、众数、中位数分别为( )
A.13,15,14 B.15,15,15
C.13.5,15,14 D.14,15,14
7.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有引起大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4 B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3 D.丁地:总体均值为2,总体方差为3
8.分层随机抽样是将总体分成若干个互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱数多少衰出之,问各几何 ”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照个人带多少钱的比例进行交税,问三人各应付多少税 则下列说法错误的是( )
A.甲应付51钱 B.乙应付32钱
C.丙应付16钱 D.三者中甲付的钱最多,丙付的钱最少
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.下关于简单随机抽样,下列说法正确的是( )
A.它要求被抽取样本的总体的个数有限 B.它是从总体中逐个地进行抽取
C.它是一种不放回抽样 D.它是一种等可能性抽样
10.有一组样本数据,,…,和一组样本数据,,…,,如果,,…,,其中为非零常数,则( )
A. 两组样本数据的样本平均数相同 B. 两组样本数据的样本方差相同
C. 两组样本数据的样本中位数相同 D. 两组样本数据的样本极差相同
11.2021年是中国共产党成立一百周年,为庆祝党的百年华诞,某校组织全体学生参加了主题为“奋斗百年路,启航新征程”的知识竞赛,随机抽取了200名学生进行成绩
统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组
后(每组的取值区间均为左闭右开区间),画出频率分布直方图(如
图),下列说法错误的是( )
A.在被抽取的学生中,成绩在区间[90,100)内的学生有75人
B.直方图中x的值为0.020
C.估计全校学生成绩的中位数为87
D.估计全校学生成绩的样本数据的80%分位数约为90
第Ⅱ卷 (非选择题 共92分)
填空题:本题共3小题,每小题5分,共15分.
12.学生在一门功课的22次考试中,所得分数如下:
56 62 63 63 65 66 68 69 71 74 76 76 77 78 79 79 82 85 87 88 95 98
则该学生该门功课考试分数的极差与中位数之和为________.
13.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生
的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
14.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9(x,y∈N),已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分13分)
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
⑴求频率分布直方图中a的值;
⑵分别求出成绩落在[50,60]与[60,70]中的学生人数.
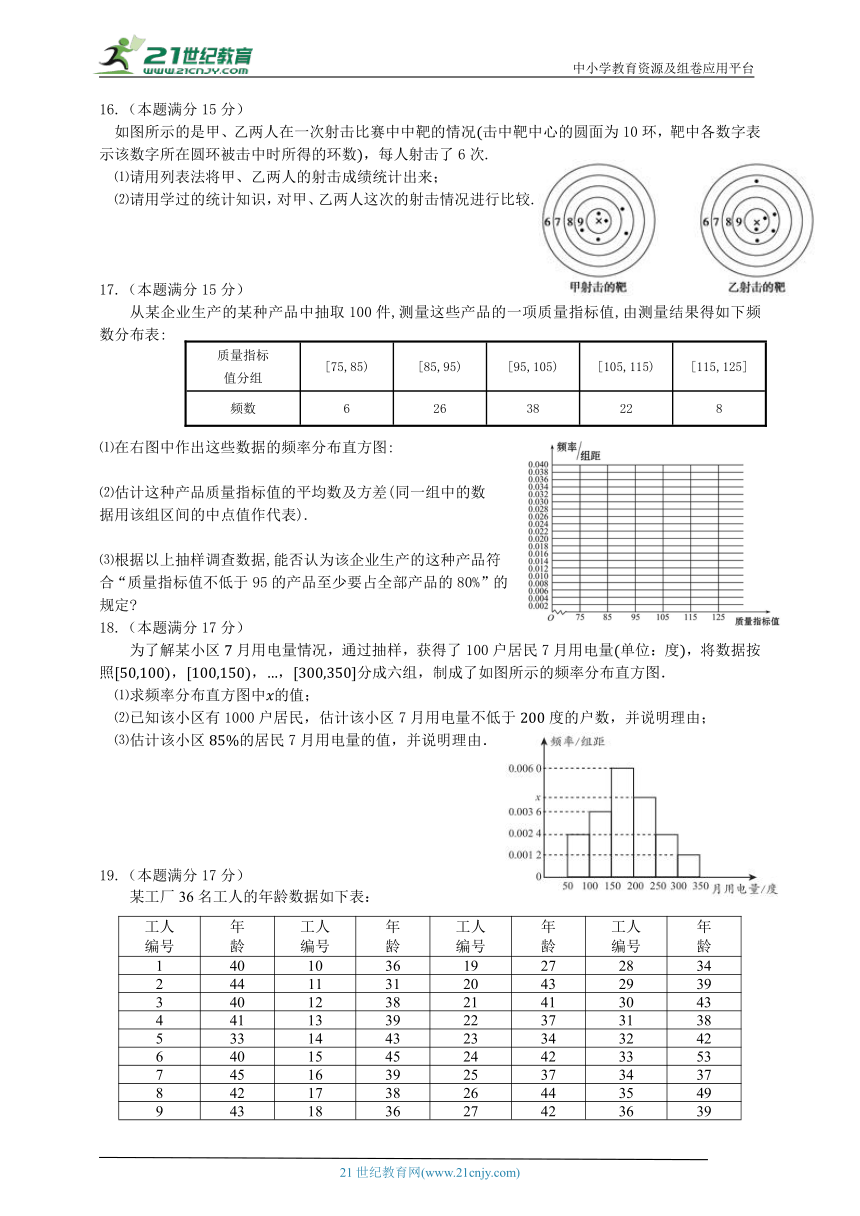
16.(本题满分15分)
如图所示的是甲、乙两人在一次射击比赛中中靶的情况击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中时所得的环数,每人射击了6次.
⑴请用列表法将甲、乙两人的射击成绩统计出来;
⑵请用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
17.(本题满分15分)
质量指标 值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
⑴在右图中作出这些数据的频率分布直方图:
⑵估计这种产品质量指标值的平均数及方差(同一组中的数
据用该组区间的中点值作代表).
⑶根据以上抽样调查数据,能否认为该企业生产的这种产品符
合“质量指标值不低于95的产品至少要占全部产品的80%”的
规定
18.(本题满分17分)
为了解某小区月用电量情况,通过抽样,获得了100户居民7月用电量单位:度,将数据按照,,,分成六组,制成了如图所示的频率分布直方图.
⑴求频率分布直方图中的值;
⑵已知该小区有1000户居民,估计该小区7月用电量不低于度的户数,并说明理由;
⑶估计该小区的居民7月用电量的值,并说明理由.
19.(本题满分17分)
某工厂36名工人的年龄数据如下表:
工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄
1 40 10 36 19 27 28 34
2 44 11 31 20 43 29 39
3 40 12 38 21 41 30 43
4 41 13 39 22 37 31 38
5 33 14 43 23 34 32 42
6 40 15 45 24 42 33 53
7 45 16 39 25 37 34 37
8 42 17 38 26 44 35 49
9 43 18 36 27 42 36 39
⑴用随机数法抽取一个容量为9的样本,并且第一次随机抽到的年龄数据为44,列出样本的年龄数据;
⑵计算(1)中样本的均值和方差s2;
⑶36名工人中年龄在-s与+s之间有多少人?所占的百分比是多少(精确到0.01%)
试题解析
选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某单位有职工160人,其中业务员104人,管理人员32人,后勤服务人员24人,现用比例分配的分层随机抽样法从中抽取一容量为20的样本,则抽取管理人员有( )
A.3人 B.4人 C.7人 D.12人
【答案】B
【解析】设管理人员x人,则160:20=32:x, ∴x=4,故选B.
2.某社团有60人,下表为此社团的年龄频数分布表,则此社团第60百分位数为( )
年龄/岁 36 38 39 43 46 48 50 55 58 60 62 65
频数 4 5 7 5 5 2 1 10 7 8 3 3
A.50 B.49 C.55 D.58
【答案】C
【解析】将60人按年龄由小到大排列,由60×60%=36,可得此社团第60百分位数为第37个数,而年龄小于等于50岁的人数为4+5+7+5+5+2+1=29人,年龄小于等于55岁的人数为29+10=39人,则第37个数为55,故选C.
3.为了解我国13岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60 m;从南方抽取了200个男孩,平均身高1.50 m,由此可推断我国13岁的男孩平均身高为( )
A.1.54 m B.1.55 m C.1.56 m D.1.57 m
【答案】C
【解析】我国13岁的男孩平均身高为(300×1.60+200×1.50)/(300+200)=1.56(m).故选C.
4.某班有50名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名学生的成绩统计有误,学生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )
A.70和67 B.70和50 C.75和50 D.75和67
【答案】A
【解析】设更正前甲、乙、……的成绩依次为a1,a2,…,a50,
则a1+a2+…+a50=50×70,即60+90+a3+…+a50=50×70,
(a1-70)2+(a2-70)2+…+(a50-70)2=50×75,即102+202+(a3-70)2+…+(a50-70)2=50×75,
更正后平均分为=×(80+70+a3+…+a50)=70;
方差为s2=×[(80-70)2+(70-70)2+(a3-70)2+…+(a50-70)2]
=×[100+(a3-70)2+…+(a50-70)2]=×(100+50×75-102-202)=67.故选A.
5某居民小区年龄在岁到岁的居民共有人,
如图是他们上网情况的频率分布直方图,现已知年龄
在的人数分别是、人,则年龄
在的频数( )
A.30 B.9
C.6 D.45
【答案】A
【解析】根据频率分布直方图得;
该居民小区年龄在[30,45)内的频率为 1-(0.02+0.06)×5=0.6,
则该年龄段的人数是 150×0.6=90人;
所以,年龄在的频数为 90-(39+21)=30.故选A.
6.统计学校排球队员的年龄,发现有12、13、14、15等四
年龄(岁) 12 13 14 15
人数(个) 2 4 6 8
种年龄,统计结果如下表:
根据表中信息可以判断该排球队员年龄的
平均数、众数、中位数分别为( )
A.13,15,14 B.15,15,15
C.13.5,15,14 D.14,15,14
【答案】D
【解析】排球队员年龄的平均数.而15出现了8次,出现的次数最多,则众数是15.从小到大排列后,排在10、11两个位置的数是14,14,则中位数是14. 故选D.
7.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有引起大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4 B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3 D.丁地:总体均值为2,总体方差为3
【答案】D
【解析】根据信息可知,连续10天内,每天新增的疑似病例不能超过7人,选项A中,中位数为4,可能存在大于7的数;同理,在选项C中也有可能;选项B中的总体方差大于0,叙述不明确,如果方差太大,也有可能存在大于7的数;选项D中,根据方差公式,如果有大于7的数存在,那么方差不可能为3.故选D.
8.分层随机抽样是将总体分成若干个互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱数多少衰出之,问各几何 ”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照个人带多少钱的比例进行交税,问三人各应付多少税 则下列说法错误的是( )
A.甲应付51钱 B.乙应付32钱
C.丙应付16钱 D.三者中甲付的钱最多,丙付的钱最少
【答案】B
【解析】由分层随机抽样方法可知,抽样比为=,
则甲应付×560=51(钱); 乙应付×350=32(钱);
丙应付×180=16(钱).故选B.
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.下关于简单随机抽样,下列说法正确的是( )
A.它要求被抽取样本的总体的个数有限 B.它是从总体中逐个地进行抽取
C.它是一种不放回抽样 D.它是一种等可能性抽样
【答案】AD
【解析】从总体中一次性批量抽取与从总体中逐个地进行抽取是等价的,则B不正确;简单随机抽样分为放回简单随机抽样与不放回简单随机抽样,则C不正确.故选AD.
10.有一组样本数据,,…,和一组样本数据,,…,,如果,,…,,其中为非零常数,则( )
A. 两组样本数据的样本平均数相同 B. 两组样本数据的样本方差相同
C. 两组样本数据的样本中位数相同 D. 两组样本数据的样本极差相同
【答案】BD
【解析】对于A,设数据,,…,的平均数为,则数据,,…,的平均数为,两组数据的平均数不相同,A错误;
对于B,设数据,,…,的方差为,则数据,,…,的方差也为,两组数据的方差相同,B正确;
对于C,设数据,,…,的中位数是,则数据,,…,的中位数是,两组数据的中位数不相同,C错误;
对于D,因为…,,为非零常数,所以数据的极差为,数据的极差为, 所以两组样本数据的极差相同,D正确.
故选BD.
11.2021年是中国共产党成立一百周年,为庆祝党的百年华诞,某校组织全体学生参加了主题为“奋斗百年路,启航新征程”的知识竞赛,随机抽取了200名学生进行成绩
统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组
后(每组的取值区间均为左闭右开区间),画出频率分布直方图(如
图),下列说法错误的是( )
A.在被抽取的学生中,成绩在区间[90,100)内的学生有75人
B.直方图中x的值为0.020
C.估计全校学生成绩的中位数为87
D.估计全校学生成绩的样本数据的80%分位数约为90
【答案】ABD
【解析】由题意,成绩在区间内的学生人数为,A错;
由,得,B错;
设中位数为,则,得,C正确;
低于分的频率为,设样本数据的分位数约为分,则,解得,D错.故选ABD.
填空题:本题共3小题,每小题5分,共15分.
12.学生在一门功课的22次考试中,所得分数如下:
56 62 63 63 65 66 68 69 71 74 76 76 77 78 79 79 82 85 87 88 95 98
则该学生该门功课考试分数的极差与中位数之和为________.
【答案】118
【解析】由题意得,最大数为98,最小数为56,极差为98-56=42,中位数为76,所以极差与中位数之和为118.
13.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生
的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个
小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校
抽取学生数为________.
【答案】80
【解析】第四组与第五组的频率和为(0.012 5+0.037 5)×5=0.25,
因为从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,
所以前三个小组的频数为36,从而男生有=48(人).
因为全校男、女生比例为3∶2,所以全校抽取学生数为48×=80.
14.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9(x,y∈N),已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
【答案】.
【解析】由这组数据的平均数为10,方差为2,可得x+y=20,(x-10)2+(y-10)2=8,
∵不要直接求出x,y,只要求出|x-y|,设x=10+t,y=10-t,
由(x-10)2+(y-10)2=8得t2=4,
∴|x-y|=2|t|=4.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
⑴求频率分布直方图中a的值;
⑵分别求出成绩落在[50,60]与[60,70]中的学生人数.
【答案】⑴0.005; ⑵2人,3人.
【解析】⑴ 据直方图知组距为10,由(2a+3a+7a+6a+2a)×10=1,
解得a==0.005.
⑵成绩落在[50,60)中的学生人数为2×0.005×10×20=2(人).
成绩落在[60,70)中的学生人数为3×0.005×10×20=3(人).
16.如图所示的是甲、乙两人在一次射击比赛中中靶的情况击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中时所得的环数,每人射击了6次.
⑴请用列表法将甲、乙两人的射击成绩统计出来;
⑵请用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
【答案】⑴详见解析; ⑵详见解析.
【解析】⑴甲、乙两人的射击成绩统计表如下:
环数 6 7 8 9 10
甲命中次数 0 0 2 2 2
乙命中次数 0 1 0 3 2
⑵=×(8×2+9×2+10×2)=9(环),
=×(7×1+9×3+10×2)=9(环),
S2甲=×[(8-9)2×2+(9-9)2×2+(10-9)2×2]=,
S2乙=×[(7-9)2+(9-9)2×3+(10-9)2×2]=1,
∵=,S2甲<S2乙,
∴甲与乙的平均成绩相同,但甲的发挥比乙稳定.
17.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标 值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
⑴在右图中作出这些数据的频率分布直方图:
⑵估计这种产品质量指标值的平均数及方差(同一组中的数
据用该组区间的中点值作代表).
⑶根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定
【答案】⑴详见解析;⑵100,104; ⑶详见解析.
【解析】⑴由频率分布表直接画出频率分布直方图:
⑵质量指标值的样本平均数为:
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为:
s2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104.
⑶质量指标值不低于95的产品所占比例的估计值为
0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定.
18.为了解某小区月用电量情况,通过抽样,获得了户居民月用电量单位:度,将数据按照,,,分成六组,制成了如图所示的频率分布直方图.
⑴求频率分布直方图中的值;
⑵已知该小区有户居民,估计该小区月用电量不低于度的户数,并说明理由;
⑶估计该小区的居民月用电量的值,并说明理由.
【答案】⑴0.0044; ⑵400;⑶262.5度.
【解析】⑴ 由频率分布直方图可得:
(0.0024+0.0036+0.0060+x+0.0024+0.0012)×50=1,
解得x=0.0044.
⑵由频率分布直方图可得,100户居民7月用电量不低于200度的频率为
(0.0044+0.0024+0.0012)×50=0.4,
由此可以估计该小区有1000户居民7月用电量不低于200度的户数为1000×0.4=400.
⑶ 由频率分布直方图可得,7月用电量低于250度的频率为0.82,7月用电量低于300度的频率为0.94,
所以85%分位数一定位于区间(250.300)内,
由250+50×=262.5.
由此估计该小区85%的居民7月用电量约为262.5度.
19.某工厂36名工人的年龄数据如下表:
工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄
1 40 10 36 19 27 28 34
2 44 11 31 20 43 29 39
3 40 12 38 21 41 30 43
4 41 13 39 22 37 31 38
5 33 14 43 23 34 32 42
6 40 15 45 24 42 33 53
7 45 16 39 25 37 34 37
8 42 17 38 26 44 35 49
9 43 18 36 27 42 36 39
⑴用随机数法抽取一个容量为9的样本,并且第一次随机抽到的年龄数据为44,列出样本的年龄数据;
⑵计算(1)中样本的均值和方差s2;
⑶36名工人中年龄在-s与+s之间有多少人?所占的百分比是多少(精确到0.01%)
【答案】⑴44,40,36,43,36,37,44,43,37;⑵40,; ⑶23人,63.89% .
【解析】⑴用随机数法抽取容量为9的样本,并且第一次随机抽到的年龄数据为44,抽取的样本如下:44,40,36,43,36,37,44,43,37.
⑵由均值公式知:==40,
由方差公式知:
s2=[(44-40)2+(40-40)2+…+(37-40)2]=.
⑶因为s2=,s=,
所以36名工人中年龄在-s与+s之间的人数等于年龄在区间[37,43]上的人数,即40,40,41,…,39,共23人.
所以36名工人中年龄在-s与+s之间的人数所占的百分比为×100%≈63.89%.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 统计 章末检测试题(含解析)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.本试卷共19小题,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题 共58分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某单位有职工160人,其中业务员104人,管理人员32人,后勤服务人员24人,现用比例分配的分层随机抽样法从中抽取一容量为20的样本,则抽取管理人员有( )
A.3人 B.4人 C.7人 D.12人
2.某社团有60人,下表为此社团的年龄频数分布表,则此社团第60百分位数为( )
年龄/岁 36 38 39 43 46 48 50 55 58 60 62 65
频数 4 5 7 5 5 2 1 10 7 8 3 3
A.50 B.49 C.55 D.58
3.为了解我国13岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60 m;从南方抽取了200个男孩,平均身高1.50 m,由此可推断我国13岁的男孩平均身高为( )
A.1.54 m B.1.55 m C.1.56 m D.1.57 m
4.某班有50名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名学生的成绩统计有误,学生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )
A.70和67 B.70和50 C.75和50 D.75和67
5.某居民小区年龄在岁到岁的居民共有人,
如图是他们上网情况的频率分布直方图,现已知年龄
在的人数分别是、人,则年龄
在的频数( )
A.30 B.9
C.6 D.45
年龄(岁) 12 13 14 15
人数(个) 2 4 6 8
6.统计学校排球队员的年龄,发现有12、13、14、15等四
种年龄,统计结果如下表:
根据表中信息可以判断该排球队员年龄的
平均数、众数、中位数分别为( )
A.13,15,14 B.15,15,15
C.13.5,15,14 D.14,15,14
7.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有引起大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4 B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3 D.丁地:总体均值为2,总体方差为3
8.分层随机抽样是将总体分成若干个互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱数多少衰出之,问各几何 ”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照个人带多少钱的比例进行交税,问三人各应付多少税 则下列说法错误的是( )
A.甲应付51钱 B.乙应付32钱
C.丙应付16钱 D.三者中甲付的钱最多,丙付的钱最少
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.下关于简单随机抽样,下列说法正确的是( )
A.它要求被抽取样本的总体的个数有限 B.它是从总体中逐个地进行抽取
C.它是一种不放回抽样 D.它是一种等可能性抽样
10.有一组样本数据,,…,和一组样本数据,,…,,如果,,…,,其中为非零常数,则( )
A. 两组样本数据的样本平均数相同 B. 两组样本数据的样本方差相同
C. 两组样本数据的样本中位数相同 D. 两组样本数据的样本极差相同
11.2021年是中国共产党成立一百周年,为庆祝党的百年华诞,某校组织全体学生参加了主题为“奋斗百年路,启航新征程”的知识竞赛,随机抽取了200名学生进行成绩
统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组
后(每组的取值区间均为左闭右开区间),画出频率分布直方图(如
图),下列说法错误的是( )
A.在被抽取的学生中,成绩在区间[90,100)内的学生有75人
B.直方图中x的值为0.020
C.估计全校学生成绩的中位数为87
D.估计全校学生成绩的样本数据的80%分位数约为90
第Ⅱ卷 (非选择题 共92分)
填空题:本题共3小题,每小题5分,共15分.
12.学生在一门功课的22次考试中,所得分数如下:
56 62 63 63 65 66 68 69 71 74 76 76 77 78 79 79 82 85 87 88 95 98
则该学生该门功课考试分数的极差与中位数之和为________.
13.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生
的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
14.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9(x,y∈N),已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分13分)
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
⑴求频率分布直方图中a的值;
⑵分别求出成绩落在[50,60]与[60,70]中的学生人数.
16.(本题满分15分)
如图所示的是甲、乙两人在一次射击比赛中中靶的情况击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中时所得的环数,每人射击了6次.
⑴请用列表法将甲、乙两人的射击成绩统计出来;
⑵请用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
17.(本题满分15分)
质量指标 值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
⑴在右图中作出这些数据的频率分布直方图:
⑵估计这种产品质量指标值的平均数及方差(同一组中的数
据用该组区间的中点值作代表).
⑶根据以上抽样调查数据,能否认为该企业生产的这种产品符
合“质量指标值不低于95的产品至少要占全部产品的80%”的
规定
18.(本题满分17分)
为了解某小区月用电量情况,通过抽样,获得了100户居民7月用电量单位:度,将数据按照,,,分成六组,制成了如图所示的频率分布直方图.
⑴求频率分布直方图中的值;
⑵已知该小区有1000户居民,估计该小区7月用电量不低于度的户数,并说明理由;
⑶估计该小区的居民7月用电量的值,并说明理由.
19.(本题满分17分)
某工厂36名工人的年龄数据如下表:
工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄
1 40 10 36 19 27 28 34
2 44 11 31 20 43 29 39
3 40 12 38 21 41 30 43
4 41 13 39 22 37 31 38
5 33 14 43 23 34 32 42
6 40 15 45 24 42 33 53
7 45 16 39 25 37 34 37
8 42 17 38 26 44 35 49
9 43 18 36 27 42 36 39
⑴用随机数法抽取一个容量为9的样本,并且第一次随机抽到的年龄数据为44,列出样本的年龄数据;
⑵计算(1)中样本的均值和方差s2;
⑶36名工人中年龄在-s与+s之间有多少人?所占的百分比是多少(精确到0.01%)
试题解析
选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某单位有职工160人,其中业务员104人,管理人员32人,后勤服务人员24人,现用比例分配的分层随机抽样法从中抽取一容量为20的样本,则抽取管理人员有( )
A.3人 B.4人 C.7人 D.12人
【答案】B
【解析】设管理人员x人,则160:20=32:x, ∴x=4,故选B.
2.某社团有60人,下表为此社团的年龄频数分布表,则此社团第60百分位数为( )
年龄/岁 36 38 39 43 46 48 50 55 58 60 62 65
频数 4 5 7 5 5 2 1 10 7 8 3 3
A.50 B.49 C.55 D.58
【答案】C
【解析】将60人按年龄由小到大排列,由60×60%=36,可得此社团第60百分位数为第37个数,而年龄小于等于50岁的人数为4+5+7+5+5+2+1=29人,年龄小于等于55岁的人数为29+10=39人,则第37个数为55,故选C.
3.为了解我国13岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60 m;从南方抽取了200个男孩,平均身高1.50 m,由此可推断我国13岁的男孩平均身高为( )
A.1.54 m B.1.55 m C.1.56 m D.1.57 m
【答案】C
【解析】我国13岁的男孩平均身高为(300×1.60+200×1.50)/(300+200)=1.56(m).故选C.
4.某班有50名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名学生的成绩统计有误,学生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )
A.70和67 B.70和50 C.75和50 D.75和67
【答案】A
【解析】设更正前甲、乙、……的成绩依次为a1,a2,…,a50,
则a1+a2+…+a50=50×70,即60+90+a3+…+a50=50×70,
(a1-70)2+(a2-70)2+…+(a50-70)2=50×75,即102+202+(a3-70)2+…+(a50-70)2=50×75,
更正后平均分为=×(80+70+a3+…+a50)=70;
方差为s2=×[(80-70)2+(70-70)2+(a3-70)2+…+(a50-70)2]
=×[100+(a3-70)2+…+(a50-70)2]=×(100+50×75-102-202)=67.故选A.
5某居民小区年龄在岁到岁的居民共有人,
如图是他们上网情况的频率分布直方图,现已知年龄
在的人数分别是、人,则年龄
在的频数( )
A.30 B.9
C.6 D.45
【答案】A
【解析】根据频率分布直方图得;
该居民小区年龄在[30,45)内的频率为 1-(0.02+0.06)×5=0.6,
则该年龄段的人数是 150×0.6=90人;
所以,年龄在的频数为 90-(39+21)=30.故选A.
6.统计学校排球队员的年龄,发现有12、13、14、15等四
年龄(岁) 12 13 14 15
人数(个) 2 4 6 8
种年龄,统计结果如下表:
根据表中信息可以判断该排球队员年龄的
平均数、众数、中位数分别为( )
A.13,15,14 B.15,15,15
C.13.5,15,14 D.14,15,14
【答案】D
【解析】排球队员年龄的平均数.而15出现了8次,出现的次数最多,则众数是15.从小到大排列后,排在10、11两个位置的数是14,14,则中位数是14. 故选D.
7.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有引起大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为3,中位数为4 B.乙地:总体均值为1,总体方差大于0
C.丙地:中位数为2,众数为3 D.丁地:总体均值为2,总体方差为3
【答案】D
【解析】根据信息可知,连续10天内,每天新增的疑似病例不能超过7人,选项A中,中位数为4,可能存在大于7的数;同理,在选项C中也有可能;选项B中的总体方差大于0,叙述不明确,如果方差太大,也有可能存在大于7的数;选项D中,根据方差公式,如果有大于7的数存在,那么方差不可能为3.故选D.
8.分层随机抽样是将总体分成若干个互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱数多少衰出之,问各几何 ”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照个人带多少钱的比例进行交税,问三人各应付多少税 则下列说法错误的是( )
A.甲应付51钱 B.乙应付32钱
C.丙应付16钱 D.三者中甲付的钱最多,丙付的钱最少
【答案】B
【解析】由分层随机抽样方法可知,抽样比为=,
则甲应付×560=51(钱); 乙应付×350=32(钱);
丙应付×180=16(钱).故选B.
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.下关于简单随机抽样,下列说法正确的是( )
A.它要求被抽取样本的总体的个数有限 B.它是从总体中逐个地进行抽取
C.它是一种不放回抽样 D.它是一种等可能性抽样
【答案】AD
【解析】从总体中一次性批量抽取与从总体中逐个地进行抽取是等价的,则B不正确;简单随机抽样分为放回简单随机抽样与不放回简单随机抽样,则C不正确.故选AD.
10.有一组样本数据,,…,和一组样本数据,,…,,如果,,…,,其中为非零常数,则( )
A. 两组样本数据的样本平均数相同 B. 两组样本数据的样本方差相同
C. 两组样本数据的样本中位数相同 D. 两组样本数据的样本极差相同
【答案】BD
【解析】对于A,设数据,,…,的平均数为,则数据,,…,的平均数为,两组数据的平均数不相同,A错误;
对于B,设数据,,…,的方差为,则数据,,…,的方差也为,两组数据的方差相同,B正确;
对于C,设数据,,…,的中位数是,则数据,,…,的中位数是,两组数据的中位数不相同,C错误;
对于D,因为…,,为非零常数,所以数据的极差为,数据的极差为, 所以两组样本数据的极差相同,D正确.
故选BD.
11.2021年是中国共产党成立一百周年,为庆祝党的百年华诞,某校组织全体学生参加了主题为“奋斗百年路,启航新征程”的知识竞赛,随机抽取了200名学生进行成绩
统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组
后(每组的取值区间均为左闭右开区间),画出频率分布直方图(如
图),下列说法错误的是( )
A.在被抽取的学生中,成绩在区间[90,100)内的学生有75人
B.直方图中x的值为0.020
C.估计全校学生成绩的中位数为87
D.估计全校学生成绩的样本数据的80%分位数约为90
【答案】ABD
【解析】由题意,成绩在区间内的学生人数为,A错;
由,得,B错;
设中位数为,则,得,C正确;
低于分的频率为,设样本数据的分位数约为分,则,解得,D错.故选ABD.
填空题:本题共3小题,每小题5分,共15分.
12.学生在一门功课的22次考试中,所得分数如下:
56 62 63 63 65 66 68 69 71 74 76 76 77 78 79 79 82 85 87 88 95 98
则该学生该门功课考试分数的极差与中位数之和为________.
【答案】118
【解析】由题意得,最大数为98,最小数为56,极差为98-56=42,中位数为76,所以极差与中位数之和为118.
13.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生
的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个
小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校
抽取学生数为________.
【答案】80
【解析】第四组与第五组的频率和为(0.012 5+0.037 5)×5=0.25,
因为从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,
所以前三个小组的频数为36,从而男生有=48(人).
因为全校男、女生比例为3∶2,所以全校抽取学生数为48×=80.
14.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9(x,y∈N),已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
【答案】.
【解析】由这组数据的平均数为10,方差为2,可得x+y=20,(x-10)2+(y-10)2=8,
∵不要直接求出x,y,只要求出|x-y|,设x=10+t,y=10-t,
由(x-10)2+(y-10)2=8得t2=4,
∴|x-y|=2|t|=4.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
⑴求频率分布直方图中a的值;
⑵分别求出成绩落在[50,60]与[60,70]中的学生人数.
【答案】⑴0.005; ⑵2人,3人.
【解析】⑴ 据直方图知组距为10,由(2a+3a+7a+6a+2a)×10=1,
解得a==0.005.
⑵成绩落在[50,60)中的学生人数为2×0.005×10×20=2(人).
成绩落在[60,70)中的学生人数为3×0.005×10×20=3(人).
16.如图所示的是甲、乙两人在一次射击比赛中中靶的情况击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中时所得的环数,每人射击了6次.
⑴请用列表法将甲、乙两人的射击成绩统计出来;
⑵请用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
【答案】⑴详见解析; ⑵详见解析.
【解析】⑴甲、乙两人的射击成绩统计表如下:
环数 6 7 8 9 10
甲命中次数 0 0 2 2 2
乙命中次数 0 1 0 3 2
⑵=×(8×2+9×2+10×2)=9(环),
=×(7×1+9×3+10×2)=9(环),
S2甲=×[(8-9)2×2+(9-9)2×2+(10-9)2×2]=,
S2乙=×[(7-9)2+(9-9)2×3+(10-9)2×2]=1,
∵=,S2甲<S2乙,
∴甲与乙的平均成绩相同,但甲的发挥比乙稳定.
17.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标 值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
⑴在右图中作出这些数据的频率分布直方图:
⑵估计这种产品质量指标值的平均数及方差(同一组中的数
据用该组区间的中点值作代表).
⑶根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定
【答案】⑴详见解析;⑵100,104; ⑶详见解析.
【解析】⑴由频率分布表直接画出频率分布直方图:
⑵质量指标值的样本平均数为:
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为:
s2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104.
⑶质量指标值不低于95的产品所占比例的估计值为
0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定.
18.为了解某小区月用电量情况,通过抽样,获得了户居民月用电量单位:度,将数据按照,,,分成六组,制成了如图所示的频率分布直方图.
⑴求频率分布直方图中的值;
⑵已知该小区有户居民,估计该小区月用电量不低于度的户数,并说明理由;
⑶估计该小区的居民月用电量的值,并说明理由.
【答案】⑴0.0044; ⑵400;⑶262.5度.
【解析】⑴ 由频率分布直方图可得:
(0.0024+0.0036+0.0060+x+0.0024+0.0012)×50=1,
解得x=0.0044.
⑵由频率分布直方图可得,100户居民7月用电量不低于200度的频率为
(0.0044+0.0024+0.0012)×50=0.4,
由此可以估计该小区有1000户居民7月用电量不低于200度的户数为1000×0.4=400.
⑶ 由频率分布直方图可得,7月用电量低于250度的频率为0.82,7月用电量低于300度的频率为0.94,
所以85%分位数一定位于区间(250.300)内,
由250+50×=262.5.
由此估计该小区85%的居民7月用电量约为262.5度.
19.某工厂36名工人的年龄数据如下表:
工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄 工人 编号 年 龄
1 40 10 36 19 27 28 34
2 44 11 31 20 43 29 39
3 40 12 38 21 41 30 43
4 41 13 39 22 37 31 38
5 33 14 43 23 34 32 42
6 40 15 45 24 42 33 53
7 45 16 39 25 37 34 37
8 42 17 38 26 44 35 49
9 43 18 36 27 42 36 39
⑴用随机数法抽取一个容量为9的样本,并且第一次随机抽到的年龄数据为44,列出样本的年龄数据;
⑵计算(1)中样本的均值和方差s2;
⑶36名工人中年龄在-s与+s之间有多少人?所占的百分比是多少(精确到0.01%)
【答案】⑴44,40,36,43,36,37,44,43,37;⑵40,; ⑶23人,63.89% .
【解析】⑴用随机数法抽取容量为9的样本,并且第一次随机抽到的年龄数据为44,抽取的样本如下:44,40,36,43,36,37,44,43,37.
⑵由均值公式知:==40,
由方差公式知:
s2=[(44-40)2+(40-40)2+…+(37-40)2]=.
⑶因为s2=,s=,
所以36名工人中年龄在-s与+s之间的人数等于年龄在区间[37,43]上的人数,即40,40,41,…,39,共23人.
所以36名工人中年龄在-s与+s之间的人数所占的百分比为×100%≈63.89%.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
