八年级数学下册沪教版 第20章《一次函数》单元复习题(含解析)
文档属性
| 名称 | 八年级数学下册沪教版 第20章《一次函数》单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 00:00:00 | ||
图片预览



文档简介
第20章《一次函数》单元复习题
一、单选题
1.在平面直角坐标系中,将一次函数的图象向左平移3个单位长度,再向下平移2个单位长度后经过点,则b的值为( )
A. B. C.2 D.4
2.如图,直线与x轴、y轴交于A、B两点,的平分线所在的直线的解析式是( )
A. B. C. D.
3.如图,直线l是一次函数的图象,且直线l过点,则下列结论错误的是( )
A.
B.直线l过坐标为的点
C.若点,在直线l上,则
D.
4.已知,一次函数的图象经过点,下列说法中不正确的是( )
A.若x满足,则当时,函数y有最小值
B.该函数的图象与坐标轴围成的三角形面积为
C.该函数的图象与一次函数的图象相互平行
D.若函数值y满足时,则自变量x的取值范围是
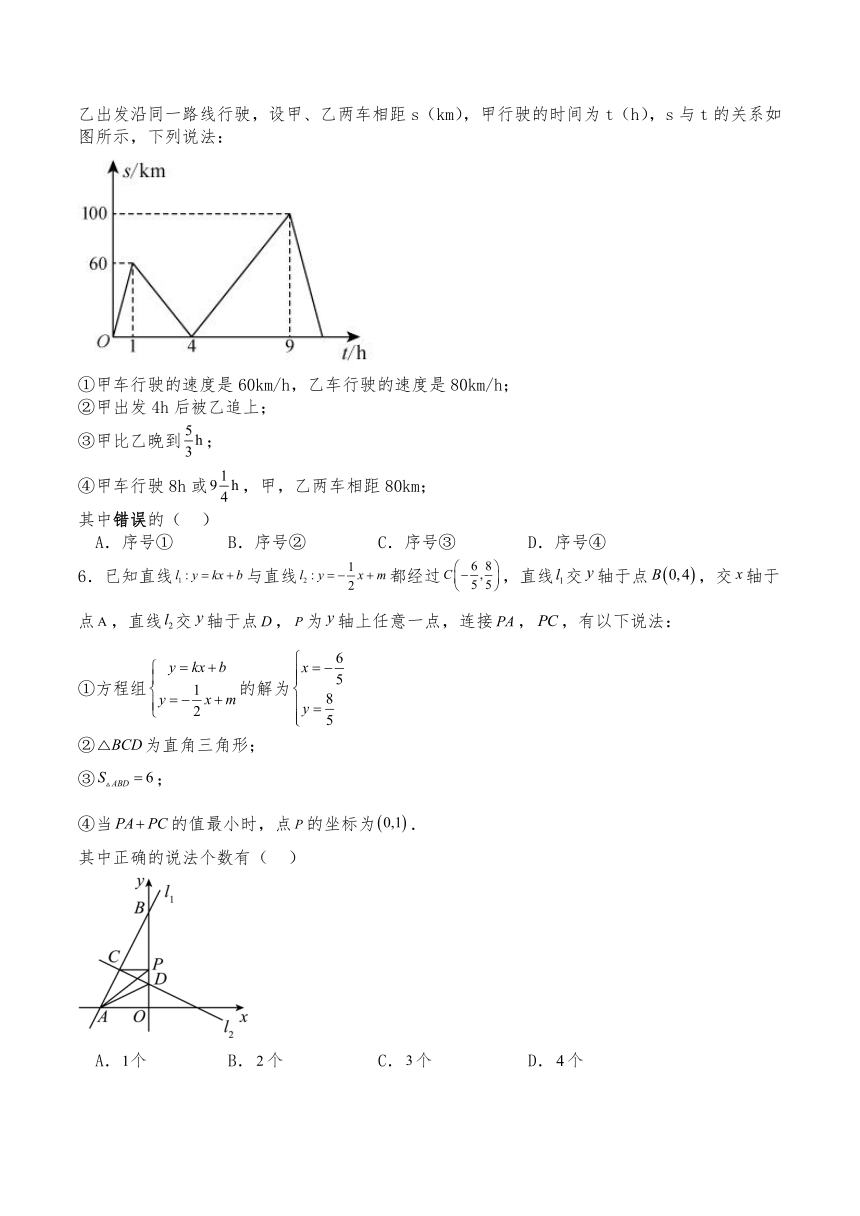
5.A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到;
④甲车行驶8h或,甲,乙两车相距80km;
其中错误的( )
A.序号① B.序号② C.序号③ D.序号④
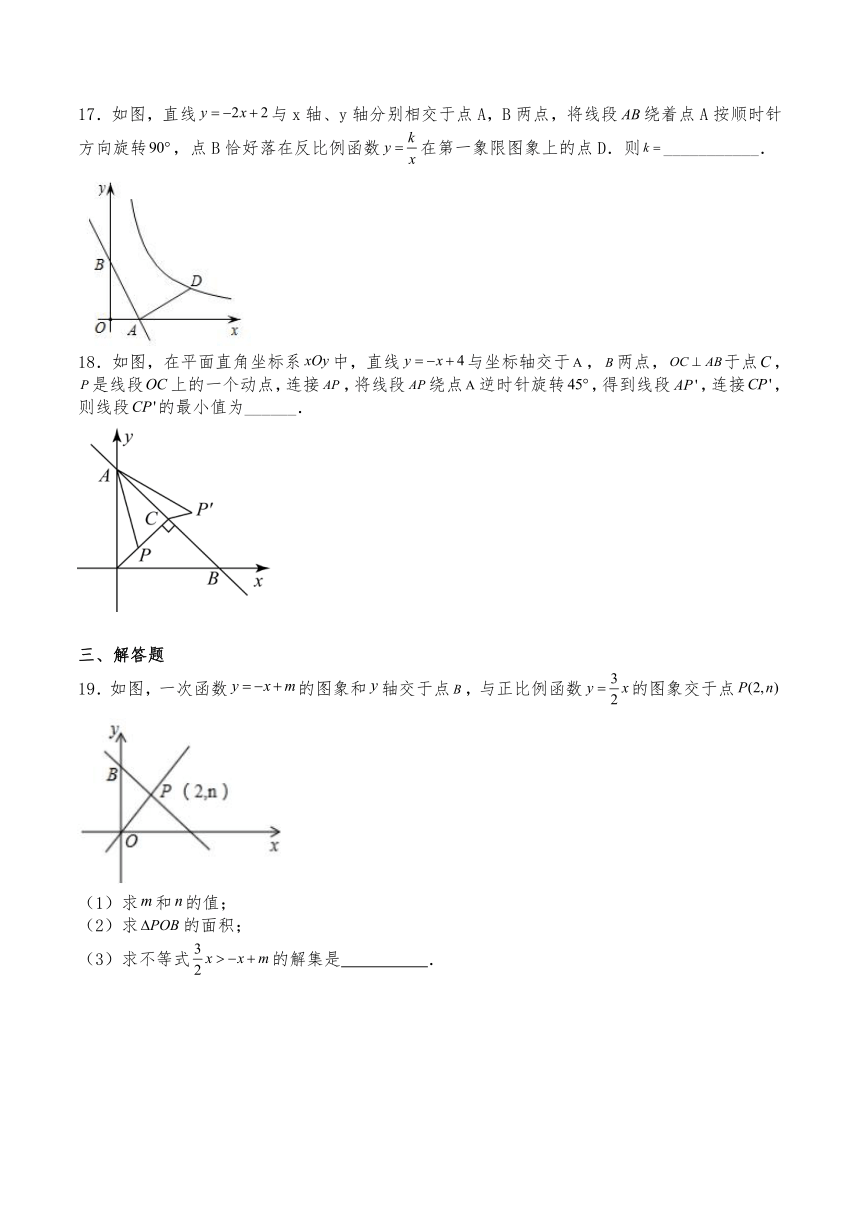
6.已知直线与直线都经过,直线交轴于点,交轴于点,直线交轴于点,为轴上任意一点,连接,,有以下说法:
①方程组的解为
②为直角三角形;
③;
④当的值最小时,点的坐标为.
其中正确的说法个数有( )
A.个 B.个 C.个 D.个
二、填空题
7.若直线与直线没有交点,则_____.
8.当时,一次函数的图像不经过第_____象限.
9.已知直线在轴上的截距为,则直线解析式为______.
10.已知直线与坐标轴围成的三角形面积是,且经过,则这条直线的表达式是______.
11.已知一次函数,原点到直线的最大距离为 _____.
12.某文具店购进一批纪念册,每本进价为20元,在销售过程中发现,该纪念册每周的销量(本)与每本的售价(元)之间满足一次函数关系:.已知某一周该纪念册的售价为每本30元,那么这一周的盈利是___________元.
13.如果,,则直线不经过______象限.
14.直线经过A(2,4),且交x轴于点B,在x轴上有一点C,令△ABC的面积为12,则C点坐标为___________________.
15.如图,的边在轴上,且,反比例函数的图象与边、分别相交于点、,连接,已知的面积为,若,直线的函数解析式为___________.
16.正方形、、;…按如图放置,其中点、、,…在x轴正半轴上,点、、…在直线上,依此类推,其中的坐标 ___________,点的坐标是 ___________.
17.如图,直线与x轴、y轴分别相交于点A,B两点,将线段绕着点A按顺时针方向旋转,点B恰好落在反比例函数在第一象限图象上的点D.则___________.
18.如图,在平面直角坐标系中,直线与坐标轴交于,两点,于点,是线段上的一个动点,连接,将线段绕点逆时针旋转,得到线段,连接,则线段的最小值为______.
三、解答题
19.如图,一次函数的图象和轴交于点,与正比例函数的图象交于点
(1)求和的值;
(2)求的面积;
(3)求不等式的解集是 .
20.如图,在平面直角坐标系中,直线与直线相交于点A,点A的横坐标为4.直线交y轴负半轴于点B,且.
(1)求点B的坐标及直线的函数表达式;
(2)现将直线沿y轴向上平移5个单位长度,交y轴于点C,交直线于点D,试求的面积.
21.如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点,且点的坐标为,
(1)求的值;
(2)若函数的函数值不大于函数的函数值,直接写出的取值范围______;
(3)求的面积.
22.已知:如图,反比例函数的图象与直线相交于点,直线与轴交于点,与轴交于点,点是的中点.
(1)求直线的函数解析式;
(2)求点到直线的距离;
(3)若点是直线上一点,且是直角三角形,求点的坐标.
23.我们研究一个新函数时,常常会借助图像研究新函数的性质,在经历“列表、描点、连线”的步骤后,就可以得到函数图像,请运用这样的方法对函数进行探究:
(1)补全表格中所缺数据,并在所给平面直角坐标系中画出函数图像.
0 1 2 3 4
1 1
(2)根据所画图像,写出该函数的两条性质:① ;② ;
(3)结合所画图像回答:当时,的取值范围是什么?
24.定义:叫做关于直线的“分边折叠函数”.
(1)已知“分边折叠函数”
①直接写出该函数与y轴的交点坐标;
②若直线与该函数只有一个交点,求t的取值范围;
(2)已知“分边折叠函数”的图像被直线与y轴所夹的线段长为,则k的值为___________.
25.在2022年卡塔尔世界杯比赛期间,国内某公司接到定制某国国家队的旗帜的任务,要求5天内完成生产53万面旗帜,该公司安排甲,乙两车间共同完成生产任务,乙车间加工过程中停工一段时间维修设备,然后提高效率继续加工,直到与甲车间同时完成加工任务为止.设甲,乙两车间各自生产旗帜y(万面)与甲车间加工时间x(天)之间的关系如图1所示;两车间未生产旗帜z(万面)与甲车间加工时间x(天)之间的关系如图2所示,请结合图象回答下列问题:
(1)甲车间每天生产旗帜___________万面,第一天甲,乙两车间共生产旗帜___________万面,___________;
(2)停工一段时间提高效率后,乙车间每天生产旗帜多少万面?
(3)当x为何值时,两车间生产的旗帜数相同?
26.如图,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点,与直线交于点E.已知点D的坐标为,点C在A的左侧且.
(1)分别求出直线和直线的表达式;
(2)在直线上,是否存在一点P,使得,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)在坐标轴上,是否存在一点Q,使得是以为直角边的直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
27.如图1,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点.直线:与直线交于点C.
(1)求直线的解析式.
(2)如图2,点P是射线上的任意一点,过点P作轴且与交于点D,连接.当时,求的面积.
(3)如图3,在(2)的条件下,将先向右平移2个单位,再向上平移4个单位,点P的对应点为点F.在x轴上确定一点G,使得以点A,F,G为顶点的三角形是等腰三角形,直接写出所有符合条件的点G的坐标.
28.在直角坐标系中,的顶点与原点重合,,.
(1)如图1,过点作轴于,过点作轴于,若点的坐标为,求点的坐标.
(2)如图2,将绕点任意旋转.若点的坐标为,求点的坐标.
(3)若点的坐标为,点的坐标为,试求,的值.
29.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
答案
一、单选题
1.B
【分析】将点,先向上平移2个单位长度,再向右平移3个单位长度,得到平移后的点,该点一次函数的图象上,利用待定系数法求出b的值即可.
【解析】解:将点,先向上平移2个单位长度,再向右平移3个单位长度,得到点,即,
由题意,得:在一次函数的图象上,
∴,
∴;
故选B.
2.B
【分析】对于已知直线,分别令与为0求出对应与的值,确定出与的坐标,在轴上取一点,使,连接,由为的平分线,得到,利用得出两三角形全等,利用全等三角形的对应边相等得到,设,可得出,在中,利用勾股定理列出关于的方程,求出方程的解得到的值,确定出坐标,设直线解析式为,将与坐标代入求出与的值,即可确定出直线解析式.
【解析】
解:对于直线,
令,求出;令求出,
,,即,,
根据勾股定理得:,
在轴上取一点,使,连接,
为的平分线,
,
在和中,
,
,
,
设,则,
在中,,
根据勾股定理得:,
解得:,
,即,
设直线解析式为,
将与坐标代入得:,
解得:,
则直线解析式为.
故选:B.
3.D
【分析】根据函数图象可知,即得出,可判断A;将点代入,即得出,即直线l的解析式为,由当时,,即可判断B;由图象可知该函数y的值随x的增大而减小,从而即可得出,可判断C正确;由该函数y的值随x的增大而减小,且当时,,即得出当时,,从而可判断D.
【解析】∵该一次函数的图象经过第二、三、四象限,且与y轴的交点位于x轴下方,
∴,
∴,故A正确,不符合题意;
将点代入,得:,
∴,
∴直线l的解析式为,
当时,,
∴直线l过坐标为的点,故B正确,不符合题意;
由图象可知该函数y的值随x的增大而减小,
又∵,
∴,故C正确,不符合题意;
∵该函数y的值随x的增大而减小,且当时,,
∴当时,,即,故D错误,符合题意.
故选D.
4.A
【分析】根据待定系数法确定一次函数的解析式,再由一次函数的性质及与坐标轴的交点依次判断即可.
【解析】解:一次函数的图象经过点,
∴,
解得:,
∴,
∵,
∴y随x的增大而减小,
A、x满足,则当时,函数y有最大值,选项错误,符合题意;
B、当时,,当时,,
∴与坐标轴的两个交点分别为,,
∴函数的图象与坐标轴围成的三角形面积为:,选项正确,不符合题意;
C、与,k都为,图象相互平行,选项正确,不符合题意;
D、当时,,解得:;
当时,,解得:;
∴函数值y满足时,则自变量x的取值范围是,选项正确,不符合题意;
故选:A.
5.D
【分析】根据图象可得甲车行驶的速度是,再由甲先出发,乙出发后追上甲,可得到乙车行驶的速度是,故①②正确;根据图象可得当乙到达地时,甲乙相距,从而得到甲比乙晚到,故③正确;然后分两种情况:当乙车在甲车前,且未到达地时和当乙车到达地后时,可得④错误.
【解析】解:①由图可得,甲车行驶的速度是,
根据图象可知:甲先出发,甲出发4h后被乙追上,
∴,
∴,
即乙车行驶的速度是,故①②正确;
③由图可得,当乙到达地时,甲乙相距,
∴甲比乙晚到,故③正确;
④由图可得,当乙车在甲车前,且未到达地时,则
解得;
当乙车到达地后时,,
解得,
∴甲车行驶或,甲,乙两车相距,故④错误;
故选:D.
6.C
【分析】根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解即可判断①;根据一次函数的解析式求得交点坐标,求得和的长,根据三角形面积计算公式,即可得到的面积,即可判断③;根据勾股定理的逆定理即可判断②;根据轴对称的性质以及两点之间,线段最短,即可得到当的值最小时,求得点P的坐标即可判断④,逐一判断即可得出答案.
【解析】解:直线与直线都经过,
方程组的解为:,故①正确;
把代入直线,可得
令,则
把,代入直线,可得
解得:
直线
令,则
,故③错误;
,,
,,
为直角三角形,故②正确;
点A关于轴对称点为
设过点,的直线为,则
解得:
令,则
当的值最小时,点P的坐标为,故④正确
故选C.
二、填空题
7.
【分析】两直线没有交点,说明两条直线平行,k值相等.
【解析】解:由题意可得,k=.
故答案为:.
8.三
【分析】根据k-1<0,k>0判断即可.
【解析】∵,
∴k-1<0,
∴函数图像一定经过第二、第四象限;
∵b=k>0,
∴图像与y轴交于正半轴,
∴函数图像一定经过第一象限;
∴函数图像一定不经过第三象限;
故答案为:三.
9.
【分析】根据题意,可得,求出的值,即可确定直线解析式.
【解析】解析:解:根据题意,得,
解得,
即直线的解析式为:,
故答案为:.
10.
【分析】先根据面积求出三角形在轴上边的长度,再分正半轴和负半轴两种情况讨论求解.
【解析】解:根据题意,设与轴交点坐标为
则,
解得,
,
当时,与轴交点为
∴,解得,
函数解析式为;
当时,与轴的交点为
∴解得,
函数解析式为.
这个一次函数的解析式是或.
故答案为:或.
11.
【分析】当时,,一次函数的图象过定点,设原点到直线的距离为d,点,根据斜边大于直角边,得到,求出的长,即为所求.
【解析】解:根据题意,设原点到直线的距离为d,
∵直线,当时,,
∴直线恒过定点,设,
则,
∴原点到直线的距离的最大值等于,
故答案为:.
12.200
【分析】将代入中得到每周的销量,再乘以单件利润即可得到答案;
【解析】解:将代入中得,
(件),
∴当纪念册的售价为每本30元,这一周的盈利是:(元);
故答案为:200.
13.第二
【分析】由,得到,,然后根据一次函数图象与系数的关系易得直线经过第一、三、四象限.
【解析】解:,,
,
,,
,,
直线经过第一、三、四象限.
故答案为:第二.
14.
【分析】将点A(2,4)代入y=kx+2,求出k,得到点B的坐标,设点C(m,0),BC=,根据△ABC的面积为12,得到,求出m,由此得到点C坐标.
【解析】解:将点A(2,4)代入y=kx+2,得2k+2=4,
解得k=1,
∴y=x+2,
当y=0时,得x+2=0,
得x=-2,
∴B(-2,0),
设点C(m,0),
∴BC=,
∵△ABC的面积为12,
∴,
解得m=4或m=-8,
∴点C的坐标为,
故答案为.
15.
【分析】连接,过作于,依据,即可得到,即可得到反比例函数为,设,则点,依据的面积为,可得,即可得出,进而得到直线的函数表达式为
【解析】解:如图,连接,过作于,
∵的面积为
∴,,
∵反比例函数的图象经过点C,
∴,
又∵,
∴,
∴反比例函数为,
∵,
∴,
∴,
∴
∴为的中点,
∴,
设,则点,
∴,
∴,
∴,即,
设的表达式为,则,即,
直线的函数表达式为
故答案为:
16.
【分析】先根据直线的解析式以及正方形的性质,设的坐标是,再根据,得出一元一次方程,解出即可得出的坐标,然后分别得出,…的坐标,据此得出点的坐标规律,即可得出答案.
【解析】解:∵四边形是正方形,
∴,
∵点在直线上,
∴设的坐标是,
∴,
解得:,
∴的坐标是,
∴点的坐标为,
∵是正方形,
∴,
∵点在直线上,
∴,
∴,
∴,
∴点的坐标为,
同理,,
可得点的坐标为,
依此类推,,
∴的坐标为.
故答案为:,.
17.3
【分析】先求出点,可得,过点D作轴于点C,证明,可得,可求出点,即可求解.
【解析】解:对于,
令,则,
令,则,
解得:,
∴点,
∴,
如图,过点D作轴于点C,
根据题意得:,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴点,
把代入得:.
故答案为:3
18.
【分析】由点的运动确定的运动轨迹是在与轴垂直的一段线段,当线段与垂直时,线段的值最小.
【解析】解:由已知可得,
三角形是等腰直角三角形,
,
,
又是线段上动点,将线段绕点逆时针旋转,
在线段上运动,所以的运动轨迹也是线段,
当在点时和在点时分别确定的起点与终点,
的运动轨迹是在与轴垂直的一段线段,
当线段与垂直时,线段的值最小,
在中,,,
,
又是等腰直角三角形,
,
.
故答案为.
三、解答题
19.(1)把代入得
所以点坐标为
把代入得得,解得
即和的值分别为;
(2)把代入得
所以点坐标为
所以的面积
(3)由图可知,因为点P的坐标为(2,3),
所以不等式x>-x+m的解集是x>2;
故答案为:x>2.
20.(1)解:点的横坐标为4,
,
点的坐标是,
,
,
,
点的坐标是,
设直线的表达式是,
则,
解得,
直线的函数表达式是;
(2)将直线沿轴向上平移5个单位长度得,
∴点C坐标为,
解得交点的横坐标为6,
.
21.(1)解:把点的坐标为代入得:
,
,
点的坐标为,
将点,点代入得:
,
解得,
一次函数的解析式为,
的值为2,的值为3,的值为;
(2)解:由(1)得点的坐标为,
由图象可得:当时,函数的函数值不大于函数的函数值,
故答案为:;
(3)解:如图所示,过点作轴交轴于点,
则点的坐标为,
函数的图象与轴交于点,
当时,,
点的坐标为,
一次函数的图象与轴交于点,
当时,,
解得,
点的坐标为,
,
的面积为.
22.(1)解:设点,
∵点是的中点,,
∴,
解得:,
∴点,
把点代入得:,
解得:,
∴直线的函数解析式为;
(2)设点到直线的距离为h,
由(1)得:点,
∴,
∵,
∴,
∴,
即,
解得:,
点到直线的距离为;
(3)设点D的坐标为,
∵点,
∴,,,
由题意知,则分两种情况讨论:
①当是以为斜边的直角三角形,
∴,
∴,
解得:,
∴点D的坐标为;
②当是以为斜边的直角三角形,
∴,
∴,
解得:,
∵当时,与重合,故舍去,
∴点D的坐标为.
综上所述:点D的坐标为,.
23.(1)当时,,
当时,,
当时,,
画出函数的图象如图:
故答案为:0,,0;
(2)由图象可知:①当时,随的增大而增大,当时,随的增大而减小,②的最小值是;
故答案为:①当时,随的增大而增大,当时,随的增大而减小,②的最小值是;
(3)由图象可得,当时,的取值范围是.
24.(1)解:①∵,,
∴当时,
∴函数与y轴的交点坐标为;
②令,代入得,
令经过点,
∴,
∴,
同理,令,代入得,
令经过点,
∴,
∴,
综上分析所得,当或时,与该函数只有一个交点;
(2)解:∵,
∴函数与y轴的交点坐标为,与直线的交点坐标为,
∵“分边折叠函数”的图像被直线与y轴所夹的线段长为,
∴,
∴,
∴(m等于0时,直线与y轴重合,不符合题意),
解得.
25.(1)由图象2可知,第一天甲乙共加工(万面),
第二天,乙停止工作,甲单独加工(万面),
则乙一天加工(万面).
∴,
故答案为:5,9,4;
(2)
=
=8(万面)
所以,停工一段时间提高效率后,乙车间每天生产旗帜8万面;
(3)设乙车间维修设备后,乙车间生产旗帜数量y(万面)与x(天)之间函数关系式为
把,代入,得,
解得,,
∴;
设甲车间生产旗帜数量y(万面)与x(天)之间函数关系式为
把代入得,
∴;
联立方程组,
∴,解得,
所以,当时,两车间生产的旗帜数相同
26.(1)解:将,代入直线:,得:
,解得:,
∴直线:,
∵,,
∴,
设直线:()
将,代入直线:,得:
,解得:,
∴直线:.
(2)解:联立,解得:,
∴,
∴,
①若点P在右侧,
∵,
∴,
∴,解得,
∴
②若点P在左侧,
∵S△BEP=8,
∴,
∴,解得,
当时,,
∴.
(3)解:分两种情况:①当时,交x轴于Q,
∵,,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
②当时,交x轴于Q,
同理,
∴,
∵,,
∴,
由勾股定理,得,
∴,
∴,
综上,存在,或.
27.(1)把,代入,得
,解得,
∴直线的解析式为;
(2)∵直线:与直线交于点C,
∴,
解得,
∴点C的横坐标为,
∴,
∵,
∴;
(3)设点,
∵轴,
∴点,
∴,
∵点P是射线上的任意一点,
解得,
∴点,
∵将先向右平移2个单位,再向上平移4个单位,点P的对应点为点F,
∴,
设,
∴,
以点A,F,G为顶点的三角形是等腰三角形有三种情况,讨论如下:
当时,即,
解得,
∴点G坐标为或;
当时,即,
解得或6(舍),
∴点G坐标为;
当时,即,
解得,
∴点G坐标为;
综上,点G坐标为或或或.
28.(1)∵,∴,.
∵轴,轴,∴.
∵,∴.
∴.
∵,∴.
∴,.
∴点的坐标为.
(2)作轴于,作轴于.
如图2,若点在第一象限,则,.
由(1),同理可证.则,.
则第四象限点为.
同理,若点在第二象限,则第一象限点为.
若点在第三象限,则第二象限点为.
若点在第四象限,则第三象限点为.
综上,若点的坐标为,点的坐标为.
(3)由(2),可得
由①,解得.
把代入②,得.
解得.检验符合.
∴,.
29.
(1)
解:对于,
当时,;当时,,
,,
在中,根据勾股定理得:,
则,;
(2)
解:过点作,垂足为(如图1所示),
平分,,,
,
在和中,
,
,
,
设,则有,,
在中,,,,
根据勾股定理得:,
解得:,
,
设直线的表达式为,
将,代入得:
,
解得:,
则直线的表达式为;
(3)
解:延长交轴于点(如图2所示),
平分,
,
又,
,
在和中,
,
,
,即为的中点,
又为直角三角形,
,
为等腰三角形,
过点作,垂足为(如图2所示),
,,
,
点的横坐标为,
设,将代入,得:,
,
则;
(4)
解:在中,,,
根据勾股定理得:,
又,(等积法),
,又,
则.
一、单选题
1.在平面直角坐标系中,将一次函数的图象向左平移3个单位长度,再向下平移2个单位长度后经过点,则b的值为( )
A. B. C.2 D.4
2.如图,直线与x轴、y轴交于A、B两点,的平分线所在的直线的解析式是( )
A. B. C. D.
3.如图,直线l是一次函数的图象,且直线l过点,则下列结论错误的是( )
A.
B.直线l过坐标为的点
C.若点,在直线l上,则
D.
4.已知,一次函数的图象经过点,下列说法中不正确的是( )
A.若x满足,则当时,函数y有最小值
B.该函数的图象与坐标轴围成的三角形面积为
C.该函数的图象与一次函数的图象相互平行
D.若函数值y满足时,则自变量x的取值范围是
5.A,B两地相距640km,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到;
④甲车行驶8h或,甲,乙两车相距80km;
其中错误的( )
A.序号① B.序号② C.序号③ D.序号④
6.已知直线与直线都经过,直线交轴于点,交轴于点,直线交轴于点,为轴上任意一点,连接,,有以下说法:
①方程组的解为
②为直角三角形;
③;
④当的值最小时,点的坐标为.
其中正确的说法个数有( )
A.个 B.个 C.个 D.个
二、填空题
7.若直线与直线没有交点,则_____.
8.当时,一次函数的图像不经过第_____象限.
9.已知直线在轴上的截距为,则直线解析式为______.
10.已知直线与坐标轴围成的三角形面积是,且经过,则这条直线的表达式是______.
11.已知一次函数,原点到直线的最大距离为 _____.
12.某文具店购进一批纪念册,每本进价为20元,在销售过程中发现,该纪念册每周的销量(本)与每本的售价(元)之间满足一次函数关系:.已知某一周该纪念册的售价为每本30元,那么这一周的盈利是___________元.
13.如果,,则直线不经过______象限.
14.直线经过A(2,4),且交x轴于点B,在x轴上有一点C,令△ABC的面积为12,则C点坐标为___________________.
15.如图,的边在轴上,且,反比例函数的图象与边、分别相交于点、,连接,已知的面积为,若,直线的函数解析式为___________.
16.正方形、、;…按如图放置,其中点、、,…在x轴正半轴上,点、、…在直线上,依此类推,其中的坐标 ___________,点的坐标是 ___________.
17.如图,直线与x轴、y轴分别相交于点A,B两点,将线段绕着点A按顺时针方向旋转,点B恰好落在反比例函数在第一象限图象上的点D.则___________.
18.如图,在平面直角坐标系中,直线与坐标轴交于,两点,于点,是线段上的一个动点,连接,将线段绕点逆时针旋转,得到线段,连接,则线段的最小值为______.
三、解答题
19.如图,一次函数的图象和轴交于点,与正比例函数的图象交于点
(1)求和的值;
(2)求的面积;
(3)求不等式的解集是 .
20.如图,在平面直角坐标系中,直线与直线相交于点A,点A的横坐标为4.直线交y轴负半轴于点B,且.
(1)求点B的坐标及直线的函数表达式;
(2)现将直线沿y轴向上平移5个单位长度,交y轴于点C,交直线于点D,试求的面积.
21.如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点,且点的坐标为,
(1)求的值;
(2)若函数的函数值不大于函数的函数值,直接写出的取值范围______;
(3)求的面积.
22.已知:如图,反比例函数的图象与直线相交于点,直线与轴交于点,与轴交于点,点是的中点.
(1)求直线的函数解析式;
(2)求点到直线的距离;
(3)若点是直线上一点,且是直角三角形,求点的坐标.
23.我们研究一个新函数时,常常会借助图像研究新函数的性质,在经历“列表、描点、连线”的步骤后,就可以得到函数图像,请运用这样的方法对函数进行探究:
(1)补全表格中所缺数据,并在所给平面直角坐标系中画出函数图像.
0 1 2 3 4
1 1
(2)根据所画图像,写出该函数的两条性质:① ;② ;
(3)结合所画图像回答:当时,的取值范围是什么?
24.定义:叫做关于直线的“分边折叠函数”.
(1)已知“分边折叠函数”
①直接写出该函数与y轴的交点坐标;
②若直线与该函数只有一个交点,求t的取值范围;
(2)已知“分边折叠函数”的图像被直线与y轴所夹的线段长为,则k的值为___________.
25.在2022年卡塔尔世界杯比赛期间,国内某公司接到定制某国国家队的旗帜的任务,要求5天内完成生产53万面旗帜,该公司安排甲,乙两车间共同完成生产任务,乙车间加工过程中停工一段时间维修设备,然后提高效率继续加工,直到与甲车间同时完成加工任务为止.设甲,乙两车间各自生产旗帜y(万面)与甲车间加工时间x(天)之间的关系如图1所示;两车间未生产旗帜z(万面)与甲车间加工时间x(天)之间的关系如图2所示,请结合图象回答下列问题:
(1)甲车间每天生产旗帜___________万面,第一天甲,乙两车间共生产旗帜___________万面,___________;
(2)停工一段时间提高效率后,乙车间每天生产旗帜多少万面?
(3)当x为何值时,两车间生产的旗帜数相同?
26.如图,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点,与直线交于点E.已知点D的坐标为,点C在A的左侧且.
(1)分别求出直线和直线的表达式;
(2)在直线上,是否存在一点P,使得,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)在坐标轴上,是否存在一点Q,使得是以为直角边的直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
27.如图1,在平面直角坐标系中,直线:与x轴交于点,与y轴交于点.直线:与直线交于点C.
(1)求直线的解析式.
(2)如图2,点P是射线上的任意一点,过点P作轴且与交于点D,连接.当时,求的面积.
(3)如图3,在(2)的条件下,将先向右平移2个单位,再向上平移4个单位,点P的对应点为点F.在x轴上确定一点G,使得以点A,F,G为顶点的三角形是等腰三角形,直接写出所有符合条件的点G的坐标.
28.在直角坐标系中,的顶点与原点重合,,.
(1)如图1,过点作轴于,过点作轴于,若点的坐标为,求点的坐标.
(2)如图2,将绕点任意旋转.若点的坐标为,求点的坐标.
(3)若点的坐标为,点的坐标为,试求,的值.
29.已知一次函数的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
(4)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
答案
一、单选题
1.B
【分析】将点,先向上平移2个单位长度,再向右平移3个单位长度,得到平移后的点,该点一次函数的图象上,利用待定系数法求出b的值即可.
【解析】解:将点,先向上平移2个单位长度,再向右平移3个单位长度,得到点,即,
由题意,得:在一次函数的图象上,
∴,
∴;
故选B.
2.B
【分析】对于已知直线,分别令与为0求出对应与的值,确定出与的坐标,在轴上取一点,使,连接,由为的平分线,得到,利用得出两三角形全等,利用全等三角形的对应边相等得到,设,可得出,在中,利用勾股定理列出关于的方程,求出方程的解得到的值,确定出坐标,设直线解析式为,将与坐标代入求出与的值,即可确定出直线解析式.
【解析】
解:对于直线,
令,求出;令求出,
,,即,,
根据勾股定理得:,
在轴上取一点,使,连接,
为的平分线,
,
在和中,
,
,
,
设,则,
在中,,
根据勾股定理得:,
解得:,
,即,
设直线解析式为,
将与坐标代入得:,
解得:,
则直线解析式为.
故选:B.
3.D
【分析】根据函数图象可知,即得出,可判断A;将点代入,即得出,即直线l的解析式为,由当时,,即可判断B;由图象可知该函数y的值随x的增大而减小,从而即可得出,可判断C正确;由该函数y的值随x的增大而减小,且当时,,即得出当时,,从而可判断D.
【解析】∵该一次函数的图象经过第二、三、四象限,且与y轴的交点位于x轴下方,
∴,
∴,故A正确,不符合题意;
将点代入,得:,
∴,
∴直线l的解析式为,
当时,,
∴直线l过坐标为的点,故B正确,不符合题意;
由图象可知该函数y的值随x的增大而减小,
又∵,
∴,故C正确,不符合题意;
∵该函数y的值随x的增大而减小,且当时,,
∴当时,,即,故D错误,符合题意.
故选D.
4.A
【分析】根据待定系数法确定一次函数的解析式,再由一次函数的性质及与坐标轴的交点依次判断即可.
【解析】解:一次函数的图象经过点,
∴,
解得:,
∴,
∵,
∴y随x的增大而减小,
A、x满足,则当时,函数y有最大值,选项错误,符合题意;
B、当时,,当时,,
∴与坐标轴的两个交点分别为,,
∴函数的图象与坐标轴围成的三角形面积为:,选项正确,不符合题意;
C、与,k都为,图象相互平行,选项正确,不符合题意;
D、当时,,解得:;
当时,,解得:;
∴函数值y满足时,则自变量x的取值范围是,选项正确,不符合题意;
故选:A.
5.D
【分析】根据图象可得甲车行驶的速度是,再由甲先出发,乙出发后追上甲,可得到乙车行驶的速度是,故①②正确;根据图象可得当乙到达地时,甲乙相距,从而得到甲比乙晚到,故③正确;然后分两种情况:当乙车在甲车前,且未到达地时和当乙车到达地后时,可得④错误.
【解析】解:①由图可得,甲车行驶的速度是,
根据图象可知:甲先出发,甲出发4h后被乙追上,
∴,
∴,
即乙车行驶的速度是,故①②正确;
③由图可得,当乙到达地时,甲乙相距,
∴甲比乙晚到,故③正确;
④由图可得,当乙车在甲车前,且未到达地时,则
解得;
当乙车到达地后时,,
解得,
∴甲车行驶或,甲,乙两车相距,故④错误;
故选:D.
6.C
【分析】根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解即可判断①;根据一次函数的解析式求得交点坐标,求得和的长,根据三角形面积计算公式,即可得到的面积,即可判断③;根据勾股定理的逆定理即可判断②;根据轴对称的性质以及两点之间,线段最短,即可得到当的值最小时,求得点P的坐标即可判断④,逐一判断即可得出答案.
【解析】解:直线与直线都经过,
方程组的解为:,故①正确;
把代入直线,可得
令,则
把,代入直线,可得
解得:
直线
令,则
,故③错误;
,,
,,
为直角三角形,故②正确;
点A关于轴对称点为
设过点,的直线为,则
解得:
令,则
当的值最小时,点P的坐标为,故④正确
故选C.
二、填空题
7.
【分析】两直线没有交点,说明两条直线平行,k值相等.
【解析】解:由题意可得,k=.
故答案为:.
8.三
【分析】根据k-1<0,k>0判断即可.
【解析】∵,
∴k-1<0,
∴函数图像一定经过第二、第四象限;
∵b=k>0,
∴图像与y轴交于正半轴,
∴函数图像一定经过第一象限;
∴函数图像一定不经过第三象限;
故答案为:三.
9.
【分析】根据题意,可得,求出的值,即可确定直线解析式.
【解析】解析:解:根据题意,得,
解得,
即直线的解析式为:,
故答案为:.
10.
【分析】先根据面积求出三角形在轴上边的长度,再分正半轴和负半轴两种情况讨论求解.
【解析】解:根据题意,设与轴交点坐标为
则,
解得,
,
当时,与轴交点为
∴,解得,
函数解析式为;
当时,与轴的交点为
∴解得,
函数解析式为.
这个一次函数的解析式是或.
故答案为:或.
11.
【分析】当时,,一次函数的图象过定点,设原点到直线的距离为d,点,根据斜边大于直角边,得到,求出的长,即为所求.
【解析】解:根据题意,设原点到直线的距离为d,
∵直线,当时,,
∴直线恒过定点,设,
则,
∴原点到直线的距离的最大值等于,
故答案为:.
12.200
【分析】将代入中得到每周的销量,再乘以单件利润即可得到答案;
【解析】解:将代入中得,
(件),
∴当纪念册的售价为每本30元,这一周的盈利是:(元);
故答案为:200.
13.第二
【分析】由,得到,,然后根据一次函数图象与系数的关系易得直线经过第一、三、四象限.
【解析】解:,,
,
,,
,,
直线经过第一、三、四象限.
故答案为:第二.
14.
【分析】将点A(2,4)代入y=kx+2,求出k,得到点B的坐标,设点C(m,0),BC=,根据△ABC的面积为12,得到,求出m,由此得到点C坐标.
【解析】解:将点A(2,4)代入y=kx+2,得2k+2=4,
解得k=1,
∴y=x+2,
当y=0时,得x+2=0,
得x=-2,
∴B(-2,0),
设点C(m,0),
∴BC=,
∵△ABC的面积为12,
∴,
解得m=4或m=-8,
∴点C的坐标为,
故答案为.
15.
【分析】连接,过作于,依据,即可得到,即可得到反比例函数为,设,则点,依据的面积为,可得,即可得出,进而得到直线的函数表达式为
【解析】解:如图,连接,过作于,
∵的面积为
∴,,
∵反比例函数的图象经过点C,
∴,
又∵,
∴,
∴反比例函数为,
∵,
∴,
∴,
∴
∴为的中点,
∴,
设,则点,
∴,
∴,
∴,即,
设的表达式为,则,即,
直线的函数表达式为
故答案为:
16.
【分析】先根据直线的解析式以及正方形的性质,设的坐标是,再根据,得出一元一次方程,解出即可得出的坐标,然后分别得出,…的坐标,据此得出点的坐标规律,即可得出答案.
【解析】解:∵四边形是正方形,
∴,
∵点在直线上,
∴设的坐标是,
∴,
解得:,
∴的坐标是,
∴点的坐标为,
∵是正方形,
∴,
∵点在直线上,
∴,
∴,
∴,
∴点的坐标为,
同理,,
可得点的坐标为,
依此类推,,
∴的坐标为.
故答案为:,.
17.3
【分析】先求出点,可得,过点D作轴于点C,证明,可得,可求出点,即可求解.
【解析】解:对于,
令,则,
令,则,
解得:,
∴点,
∴,
如图,过点D作轴于点C,
根据题意得:,,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴点,
把代入得:.
故答案为:3
18.
【分析】由点的运动确定的运动轨迹是在与轴垂直的一段线段,当线段与垂直时,线段的值最小.
【解析】解:由已知可得,
三角形是等腰直角三角形,
,
,
又是线段上动点,将线段绕点逆时针旋转,
在线段上运动,所以的运动轨迹也是线段,
当在点时和在点时分别确定的起点与终点,
的运动轨迹是在与轴垂直的一段线段,
当线段与垂直时,线段的值最小,
在中,,,
,
又是等腰直角三角形,
,
.
故答案为.
三、解答题
19.(1)把代入得
所以点坐标为
把代入得得,解得
即和的值分别为;
(2)把代入得
所以点坐标为
所以的面积
(3)由图可知,因为点P的坐标为(2,3),
所以不等式x>-x+m的解集是x>2;
故答案为:x>2.
20.(1)解:点的横坐标为4,
,
点的坐标是,
,
,
,
点的坐标是,
设直线的表达式是,
则,
解得,
直线的函数表达式是;
(2)将直线沿轴向上平移5个单位长度得,
∴点C坐标为,
解得交点的横坐标为6,
.
21.(1)解:把点的坐标为代入得:
,
,
点的坐标为,
将点,点代入得:
,
解得,
一次函数的解析式为,
的值为2,的值为3,的值为;
(2)解:由(1)得点的坐标为,
由图象可得:当时,函数的函数值不大于函数的函数值,
故答案为:;
(3)解:如图所示,过点作轴交轴于点,
则点的坐标为,
函数的图象与轴交于点,
当时,,
点的坐标为,
一次函数的图象与轴交于点,
当时,,
解得,
点的坐标为,
,
的面积为.
22.(1)解:设点,
∵点是的中点,,
∴,
解得:,
∴点,
把点代入得:,
解得:,
∴直线的函数解析式为;
(2)设点到直线的距离为h,
由(1)得:点,
∴,
∵,
∴,
∴,
即,
解得:,
点到直线的距离为;
(3)设点D的坐标为,
∵点,
∴,,,
由题意知,则分两种情况讨论:
①当是以为斜边的直角三角形,
∴,
∴,
解得:,
∴点D的坐标为;
②当是以为斜边的直角三角形,
∴,
∴,
解得:,
∵当时,与重合,故舍去,
∴点D的坐标为.
综上所述:点D的坐标为,.
23.(1)当时,,
当时,,
当时,,
画出函数的图象如图:
故答案为:0,,0;
(2)由图象可知:①当时,随的增大而增大,当时,随的增大而减小,②的最小值是;
故答案为:①当时,随的增大而增大,当时,随的增大而减小,②的最小值是;
(3)由图象可得,当时,的取值范围是.
24.(1)解:①∵,,
∴当时,
∴函数与y轴的交点坐标为;
②令,代入得,
令经过点,
∴,
∴,
同理,令,代入得,
令经过点,
∴,
∴,
综上分析所得,当或时,与该函数只有一个交点;
(2)解:∵,
∴函数与y轴的交点坐标为,与直线的交点坐标为,
∵“分边折叠函数”的图像被直线与y轴所夹的线段长为,
∴,
∴,
∴(m等于0时,直线与y轴重合,不符合题意),
解得.
25.(1)由图象2可知,第一天甲乙共加工(万面),
第二天,乙停止工作,甲单独加工(万面),
则乙一天加工(万面).
∴,
故答案为:5,9,4;
(2)
=
=8(万面)
所以,停工一段时间提高效率后,乙车间每天生产旗帜8万面;
(3)设乙车间维修设备后,乙车间生产旗帜数量y(万面)与x(天)之间函数关系式为
把,代入,得,
解得,,
∴;
设甲车间生产旗帜数量y(万面)与x(天)之间函数关系式为
把代入得,
∴;
联立方程组,
∴,解得,
所以,当时,两车间生产的旗帜数相同
26.(1)解:将,代入直线:,得:
,解得:,
∴直线:,
∵,,
∴,
设直线:()
将,代入直线:,得:
,解得:,
∴直线:.
(2)解:联立,解得:,
∴,
∴,
①若点P在右侧,
∵,
∴,
∴,解得,
∴
②若点P在左侧,
∵S△BEP=8,
∴,
∴,解得,
当时,,
∴.
(3)解:分两种情况:①当时,交x轴于Q,
∵,,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
②当时,交x轴于Q,
同理,
∴,
∵,,
∴,
由勾股定理,得,
∴,
∴,
综上,存在,或.
27.(1)把,代入,得
,解得,
∴直线的解析式为;
(2)∵直线:与直线交于点C,
∴,
解得,
∴点C的横坐标为,
∴,
∵,
∴;
(3)设点,
∵轴,
∴点,
∴,
∵点P是射线上的任意一点,
解得,
∴点,
∵将先向右平移2个单位,再向上平移4个单位,点P的对应点为点F,
∴,
设,
∴,
以点A,F,G为顶点的三角形是等腰三角形有三种情况,讨论如下:
当时,即,
解得,
∴点G坐标为或;
当时,即,
解得或6(舍),
∴点G坐标为;
当时,即,
解得,
∴点G坐标为;
综上,点G坐标为或或或.
28.(1)∵,∴,.
∵轴,轴,∴.
∵,∴.
∴.
∵,∴.
∴,.
∴点的坐标为.
(2)作轴于,作轴于.
如图2,若点在第一象限,则,.
由(1),同理可证.则,.
则第四象限点为.
同理,若点在第二象限,则第一象限点为.
若点在第三象限,则第二象限点为.
若点在第四象限,则第三象限点为.
综上,若点的坐标为,点的坐标为.
(3)由(2),可得
由①,解得.
把代入②,得.
解得.检验符合.
∴,.
29.
(1)
解:对于,
当时,;当时,,
,,
在中,根据勾股定理得:,
则,;
(2)
解:过点作,垂足为(如图1所示),
平分,,,
,
在和中,
,
,
,
设,则有,,
在中,,,,
根据勾股定理得:,
解得:,
,
设直线的表达式为,
将,代入得:
,
解得:,
则直线的表达式为;
(3)
解:延长交轴于点(如图2所示),
平分,
,
又,
,
在和中,
,
,
,即为的中点,
又为直角三角形,
,
为等腰三角形,
过点作,垂足为(如图2所示),
,,
,
点的横坐标为,
设,将代入,得:,
,
则;
(4)
解:在中,,,
根据勾股定理得:,
又,(等积法),
,又,
则.
