七年级数学下册沪教版 第14章《三角形》单元复习题(含解析)
文档属性
| 名称 | 七年级数学下册沪教版 第14章《三角形》单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 358.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 20:42:31 | ||
图片预览


文档简介
第14章《三角形》单元复习题
一.选择题
1.在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是( )
A.0<AD<12 B.1<AD<6 C.0<AD<6 D.2<AD<12
2.下列不能作为判定△ABC≌△DEF的条件是( )
A.AB=DE,BC=EF,∠B=∠E B.∠A=∠D,AB=DE,∠B=∠E
C.AB=DE,BC=EF,∠A=∠D D.∠A=∠D,AC=DF,∠B=∠E
3.已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
4.如图,在△ABC中,AD垂直BC于D,BE垂直AC于E,AD、BE交于点H,且HD=DC,那么下列结论中,正确的是( )
A.AH=BD B.△AHE≌△BHD C.△ADC≌△BDH D.HE=EC
二.填空题
5.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 度.
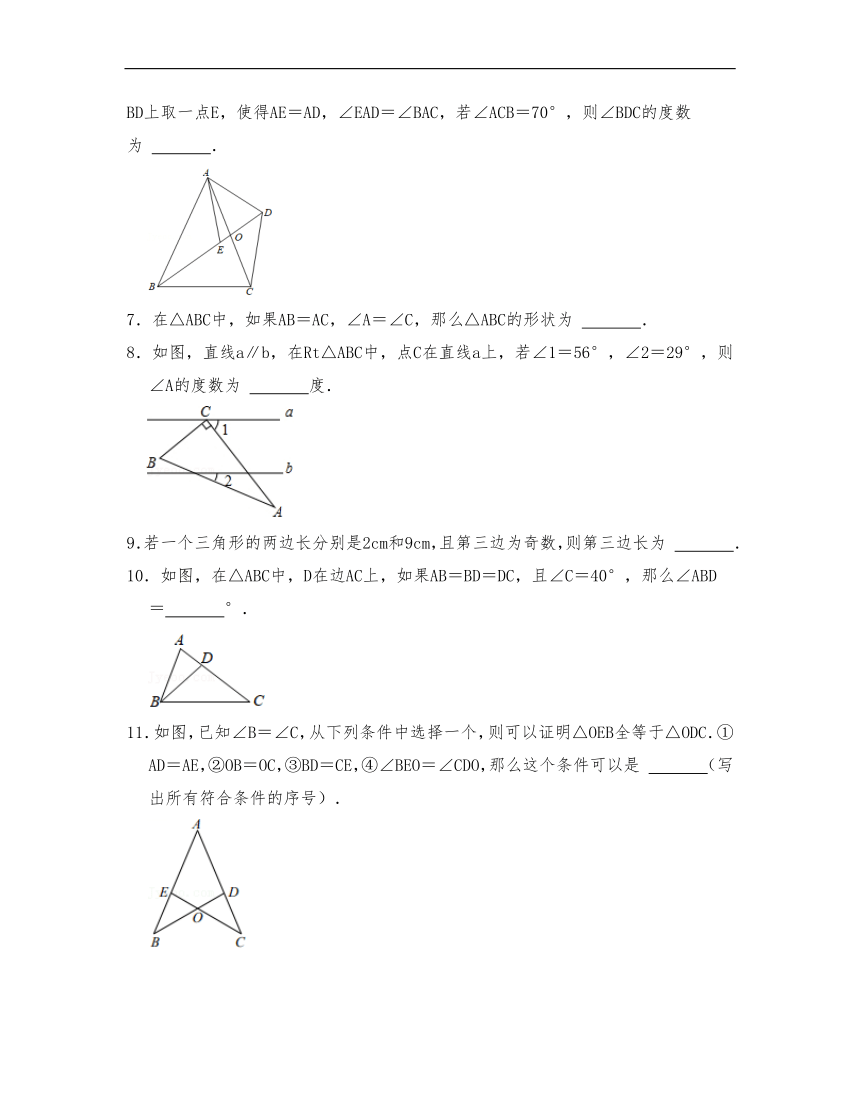
6.在△ABC中,AB=AC,点D是△ABC外一点,连接AD、BD、CD,且BD交AC于点O,在BD上取一点E,使得AE=AD,∠EAD=∠BAC,若∠ACB=70°,则∠BDC的度数为 .
7.在△ABC中,如果AB=AC,∠A=∠C,那么△ABC的形状为 .
8.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 度.
9.若一个三角形的两边长分别是2cm和9cm,且第三边为奇数,则第三边长为 .
10.如图,在△ABC中,D在边AC上,如果AB=BD=DC,且∠C=40°,那么∠ABD= °.
11.如图,已知∠B=∠C,从下列条件中选择一个,则可以证明△OEB全等于△ODC.①AD=AE,②OB=OC,③BD=CE,④∠BEO=∠CDO,那么这个条件可以是 (写出所有符合条件的序号).
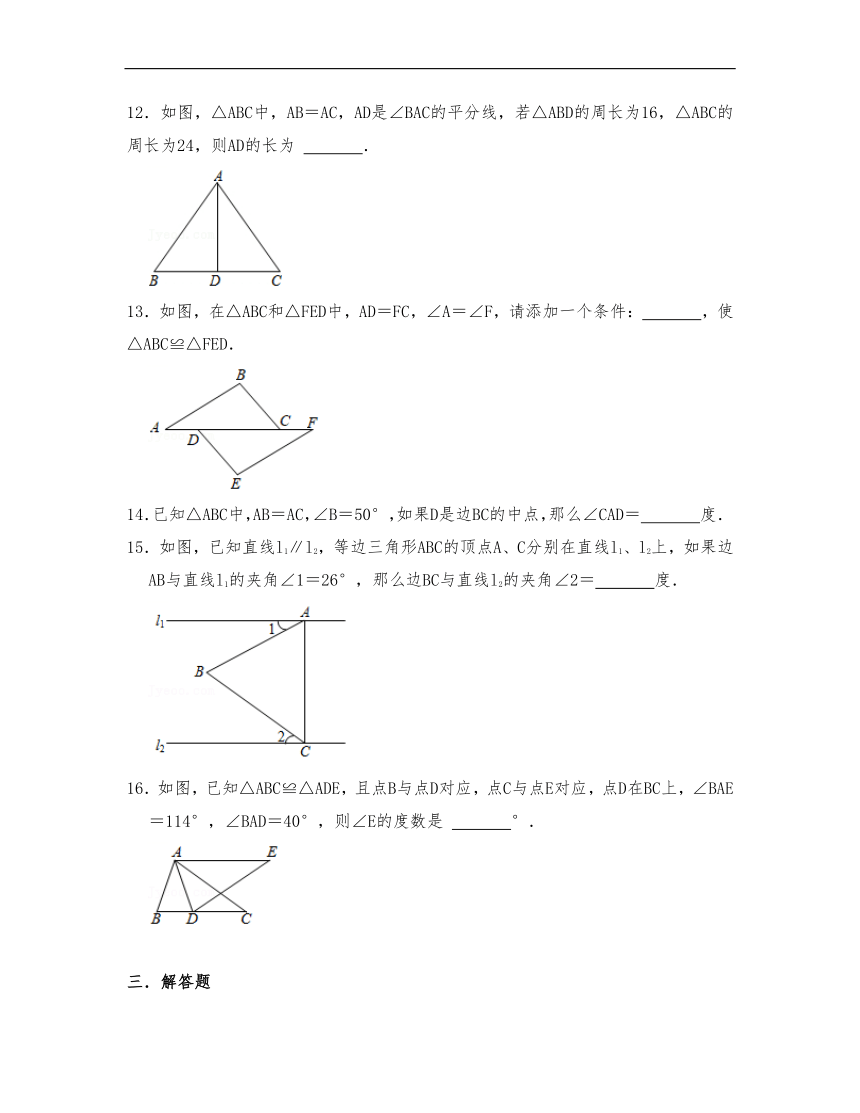
12.如图,△ABC中,AB=AC,AD是∠BAC的平分线,若△ABD的周长为16,△ABC的周长为24,则AD的长为 .
13.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件: ,使△ABC≌△FED.
14.已知△ABC中,AB=AC,∠B=50°,如果D是边BC的中点,那么∠CAD= 度.
15.如图,已知直线l1∥l2,等边三角形ABC的顶点A、C分别在直线l1、l2上,如果边AB与直线l1的夹角∠1=26°,那么边BC与直线l2的夹角∠2= 度.
16.如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 °.
三.解答题
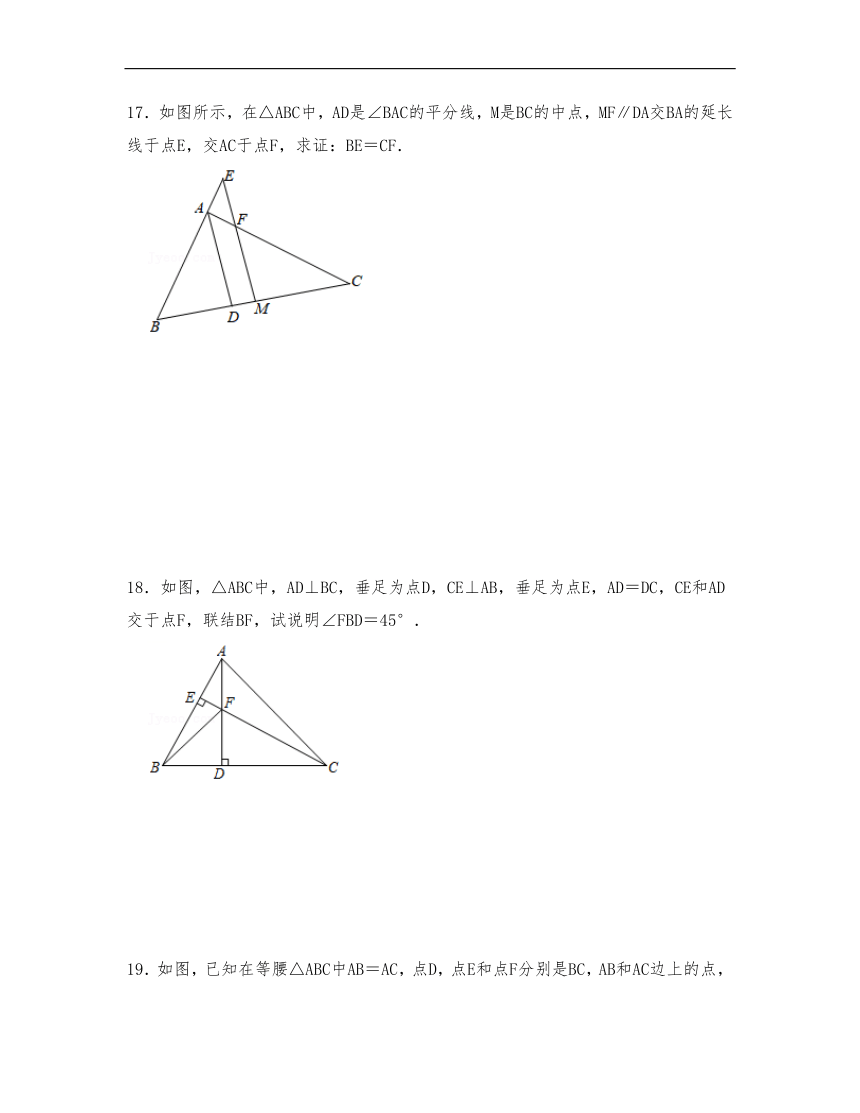
17.如图所示,在△ABC中,AD是∠BAC的平分线,M是BC的中点,MF∥DA交BA的延长线于点E,交AC于点F,求证:BE=CF.
18.如图,△ABC中,AD⊥BC,垂足为点D,CE⊥AB,垂足为点E,AD=DC,CE和AD交于点F,联结BF,试说明∠FBD=45°.
19.如图,已知在等腰△ABC中AB=AC,点D,点E和点F分别是BC,AB和AC边上的点,且BE=DC,∠B=∠EDF,试说明DE=DF.
20.如图,在△ABC中,点D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.试说明AD=ED的理由.
解:因为CE∥AB(已知),
所以∠BAD= ( ).
因为点D是边BC的中点,
所以 ,
在△ABD和△ECD中,
,
所以△ABD≌△ECD( ),
所以AD=ED( ).
21.如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
22.如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
23.如图,已知AD=BC,AE=BE,说明AC=BD的理由.
24.如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
25.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
26.如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,过点B作BE⊥AC,垂足为E,在线段BE上截取ED=EC,AD的延长线交BC于点P,联结DC.
(1)请说明AD=BC的理由;
(2)请说明BP=PC的理由.
27.如图,已知在△ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠ADE的度数.
28.如图,已知直线AB∥CD,∠ACD的平分线CE交AB于点F,∠AFE的平分线交CA延长线于点G.
(1)说明AC=AF的理由;
(2)若∠FCD=32°,求∠G的大小.
29.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
30.已知在△ABC与△CDE中,AB=CD,∠B=∠D,∠ACE=∠B,点B、C、D在同一直线上,射线AH、EI分别平分∠BAC、∠CED.
(1)如图1,试说明AC=CE的理由;
(2)如图2,当AH、EI交于点G时,设∠B=α,∠AGE=β,求β与α的数量关系,并说明理由;
(3)当AH∥EI时,求∠B的度数.
答案
一.选择题
1.
【分析】作出图形,延长中线AD到E,使DE=AD,利用“边角边”证明△ACD和△EBD全等,根据全等三角形对应边相等可得AC=BE,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE的范围,再除以2即可得解.
【解答】解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7﹣5<AE<7+5,
即7﹣5<2AD<7+5,
∴1<AD<6.
故选:B.
2.
【分析】根据全等三角形的判定方法判断即可.
【解答】解:A、AB=DE,BC=EF,∠B=∠E,可以利用SAS判定△ABC≌△DEF,不符合题意;
B、∠A=∠D,AB=DE,∠B=∠E,可以利用ASA判定△ABC≌△DEF,不符合题意;
C、AB=DE,BC=EF,∠A=∠D,不能利用SSA判定△ABC≌△DEF,符合题意;
D、∠A=∠D,AC=DF,∠B=∠E,可以利用AAS判定△ABC≌△DEF,不符合题意;
故选:C.
3.
【分析】根据各个选项给出的条件结合三角形内角和定理,即三角形内角和等于180°,推导出三角形中是否存在90°的内角.若存在,则△ABC是直角三角形.若不存在,则△ABC不是直角三角形.
【解答】解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
4.
【分析】首先根据垂直可得∠ADB=∠ADC=90°,然后再证明∠HAE=∠HBD,然后再利用AAS证明△ADC≌△BDH.
【解答】解:∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∴∠DAE+∠AHE=90°,
∵BE⊥AC,
∴∠HBD+∠BHD=90°,
∵∠AHE=∠BHD,
∴∠HAE=∠HBD,
在△ADC和△BDH中,
,
∴△ADC≌△BDH(AAS),
故选:C.
二.填空题
5.
【分析】根据平行线的性质及可得到答案.
【解答】解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=126°,∠2=80°,
∴∠3=∠1﹣∠2=46°,
故答案为:46.
6.
【分析】根据SAS证明△ABE≌△ACD,再利用全等三角形的性质、三角形的外角性质和三角形的内角和解答即可.
【解答】解:∵∠EAD=∠BAC,
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD (SAS),
∴∠ABD=∠ACD,
∵∠BOC是△ABO和△DCO的外角,
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC,
∴∠ABD+∠BAC=∠ACD+∠BDC,
∴∠BAC=∠BDC,
∵∠ACB=70°,AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°,
∴∠BDC=∠BAC=40°.
故答案为:40°.
7.
【分析】可利用等腰三角形的判定,说明三角形的三条边都相等,亦可利用等腰三角形的性质,说明该三角形的三个角都相等.
【解答】解:(法一)在△ABC中,∵∠A=∠C,
∴BA=BC.
又∵AB=AC,
AB=AC=BC.
所以△ABC是等边三角形.
故答案为:等边三角形.
(法二)在△ABC中,∵AB=AC,
∴∠B=∠C.
又∵∠A=∠C,
∴∠A=∠B=∠C.
所以△ABC是等边三角形.
故答案为:等边三角形.
8.
【分析】先根据对顶角的定义得出∠3的度数,再由三角形内角与外角的关系求出∠A的度数.
【解答】解:如图,
∵直线a∥b,
∴∠3=∠1,
∵∠1=56°,
∴∠3=56°,
∵∠3=∠2+∠A,∠2=29°,
∴∠A=∠3﹣∠2=56°﹣29°=27°.
故答案为:27.
9.
【分析】根据三角形的三边关系求得第三边的取值范围,再根据第三边是奇数求得第三边的长.
【解答】解:设第三边长xcm.
根据三角形的三边关系,得7<x<11.
又∵三角形的第三边长是奇数,因而满足条件的数是9cm.
故答案为:9cm.
10.
【分析】由等腰三角形的性质可得∠DBC=∠C=40°,由三角形的内角和定理可得∠BDC=180°﹣40°﹣40°=100°,由邻补角的性质可得∠ADB,易得∠A,从而求得∠ABD.
【解答】解:∵AB=BD=DC,∠C=40°,
∴∠DBC=∠C=40°,∠A=∠ADB,
∴∠BDC=180°﹣40°﹣40°=100°,
∴∠ADB=180°﹣100°=80°,
∴∠A=80°,
∴∠ABD=180°﹣∠ADB﹣∠A=180°﹣80°﹣80°=20°,
故答案为:20.
11.
【分析】根据全等三角形的判定方法解答即可.
【解答】解:选择①和②可与∠B=∠C一起得出△ABD≌△ACE(AAS),选择③可与∠B=∠C一起得出△ABD≌△ACE(AAS),
∴AB=AC,AD=AE,
∴BE=CD,
∴△OEB≌△ODC(AAS)
选择④没有已知的边,不能得到△OEB≌△ODC,
故答案为:①或②或③.
12.
【分析】先由等腰三角形三线合一的性质得出BD=CD,再根据△ABD的周长为16,得到AB+BD+AD=16,即AB+AC+BC+2AD=32,再将AB+AC+BC=24代入,即可求出AD的长.
【解答】解:∵△ABC中,AB=AC,AD是∠BAC的平分线,
∴BD=CD.
∵△ABD的周长为16,
∴AB+BD+AD=16,
∴2AB+2BD+2AD=32,
∴AB+AC+BC+2AD=32,
∵△ABC的周长为24,
∴AB+AC+BC=24,
∴24+2AD=32,
∴AD=4.
故答案为4
13.
【分析】根据三角形的判定定理:SSS、SAS、AAS进行判断即可.
【解答】解:∵AD=FC,
∴AC=FD,
∵∠A=∠F,
∴添加AB=FE,利用SAS得出△ABC≌△FED,
添加∠B=∠E,利用AAS得出△ABC≌△FED,
添加∠ACB=∠FDE,利用ASA得出△ABC≌△FED,
添加DE∥BC,得出∠EDF=∠BCA,利用ASA得出△ABC≌△FED,
故答案为:AB=FE或∠B=∠E或∠ACB=∠FDE或DE∥BC.
14.
【分析】首先利用等腰三角形的底角的度数求得另一个底角的度数,然后根据等腰三角形“三线合一”的性质求得答案即可.
【解答】解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∵D是边BC的中点,
∴AD⊥BC,
∴∠CAD=40°,
故答案为:40.
15.
【分析】由等边三角形的性质得∠BAC=∠BCA=60°,再由平行线的性质得∠1+∠BAC+∠BCA+∠2=180°,则∠1+∠2=60°,即可求解.
【解答】解:∵△ABC是等边三角形,
∴∠BAC=∠BCA=60°,
∵直线l1∥l2,
∴∠1+∠BAC+∠BCA+∠2=180°,
∴∠1+∠2=180°﹣60°﹣60°=60°,
∵∠1=26°,
∴∠2=60°﹣26°=34°,
故答案为:34.
16.
【分析】根据全等三角形的性质得出AB=AD,∠ABD=∠ADE,根据等腰三角形的性质和三角形内角和定理求出∠ABD=70°,求出∠DAE和∠ADE,再根据三角形内角和定理求出∠E即可.
【解答】解:∵△ABC≌△ADE,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠BAD=40°,
∴∠ABD=∠ADB=(180°﹣∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36.
三.解答题
17.证明:如图,过点B作BN∥AC交EM的延长线于N,
∴∠MBN=∠C,∠N=∠MFC,
∵M为BC的中点,
∴BM=CM,
在△BMN和△CMF中,
,
∴△BMN≌△CMF(AAS),
∴BN=CF,
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵ME∥AD,
∴∠E=∠BAD,∠MFC=∠CAD,
∴∠E=∠MFC,
∴∠E=∠N,
∴BE=BN,
∴BE=CF.
18.解:∵AD⊥BC,CE⊥AB,
∴∠ADC=∠ADB=90°=∠CEB,
∴∠ABD+∠BAD=90°=∠BCE+∠ABD,
∴∠BAD=∠BCE,
在△ABD和△CFD中,
,
∴△ABD≌△CFD(ASA),
∴BD=DF,
又∵∠ADB=90°,
∴∠FBD=45°.
19.解:∵AB=AC,
∴∠B=∠C,
∵∠B=∠EDF,
∴∠C=∠EDF,
∵∠EDC=∠B+∠BED=∠EDF+∠FDC,
∴∠BED=∠CDF,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(ASA),
∴DE=DF.
20.解:因为CE∥AB(已知),
所以∠BAD=∠E(两直线平行,内错角相等).
因为点D是边BC的中点,
所以BD=CD,
在△ABD和△ECD中,
所以△ABD≌△ECD(AAS),
所以AD=ED(全等三角形的对应边相等).
故答案为∠E,两直线平行,内错角相等;∠BAD=∠E,对顶角相等,BD=CD;AAS;全等三角形的对应边相等.
21.解:∵AE⊥DE,
∴∠AED=90°,
又∵∠B=90°,
∴∠B=∠AED,
∵∠AEC=∠B+∠BAE,
即∠AED+∠DEC=∠B+∠BAE,
∴∠BAE=∠DEC,
在△ABE与△ECD中,
,
∴△ABE≌△ECD(ASA),
∴AE=ED,
∵EF⊥AD,
∴点F是AD的中点.
22.解:∠B与∠C相等,
理由:∵∠FDC=∠FDE+∠EDC,
又∵∠FDC=∠B+∠BFD,
∴∠FDE+∠EDC=∠B+∠BFD,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
在△BFD和△CDE中
,
∴△BFD≌△CDE(SAS),
∴∠B=∠C.
23.证明:∵AD=BC,AE=BE,
∴AD﹣AE=BC﹣BE,
即DE=CE,
在△ACE与△BDE中,
,
∴△ACE≌△BDE(SAS),
∴AC=BD.
24.解:∵AB=BD,
∴∠BAD=∠BDA,
∵∠ADE=∠B,∠ADE+∠BAD+∠AED=180°,∠B+∠BDA+∠BAD=180°,
∴∠AED=∠BAD,
∴ED=AD,
∴△ADE为等腰三角形.
25.解:AB+BE=CD,理由如下:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴AB=DE,BD=CD,
∵DE+BE=BD,
∴AB+BE=CD.
26.解:(1)∵BE⊥AC,∠BAC=45°,
∴∠ABE=90°﹣45°=45°,
∴BE=AE,
在△BCE和△ADE中,
,
∴△BCE≌△ADE(SAS),
∴AD=BC.
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵BE⊥AC,BE=AE,EC=ED,
∴∠DCE=∠CDE=∠EBA=∠BAE=45°,
∴∠ABC﹣∠EBA=∠ACB﹣∠DCE,即∠DBC=∠DCB,
∴BD=CD,
∴PD为线段BC的垂直平分线,
∴BP=PC.
27.解:∵AB=AC,∠BAC=80°,AD⊥BC,
∴∠BAD=∠CAD=∠BAC=40°,
∵AD=AB,
∴∠BDA=×(180°﹣40°)=70°,
∴∠ADE=180°﹣∠BDA=180°﹣70°=110°.
28.(1)证明:∵∠ACD的平分线CE交AB于点F,
∴∠ACF=∠DCF,
∵AB∥CD,
∴∠AFC=∠DCF,
∴∠ACF=∠AFC,
∴AC=AF;
(2)解:∵∠FCD=32°,AB∥CD,
∴∠ACD=∠GAF=64°,∠AFC=32°,
∵∠AFE的平分线交CA延长线于点G.
∴∠AFG=∠GFE=AFE=,
∴∠G=180°﹣∠GAF﹣∠AFG=180°﹣64°﹣74°=42°.
29.解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
30.(1)证明:∵∠ACD=∠ACE+∠ECD=∠A+∠B,
又∠B=∠ACE,
∴∠A=∠ECD.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA).
∴AC=CE.
(2)解:3α﹣2β=180°.理由如下:
如图1所示,连接GC并延长至点K.
∵AH、EI分别平分∠BAC、∠DEC,
则设∠CAH=∠BAH=a,∠CEI=∠DEI=b,
∵∠ACK为△ACG的外角,
∴∠ACK=a+∠AGC,
同理可得∠ECK=b+∠EGC,
∴∠ACE=∠ACK+∠ECK=∠B=α
=(a+∠AGC)+(b+∠EGC)=a+b+∠AGE=a+b+β,
即α=a+b+β,
∴a+b=α﹣β.
又由(1)中证明可知∠ECD=∠BAC=2a,
由三角形内角和公式可得∠ECD+∠DEC+∠D=180°,
即2a+2b+α=180°,
∴2(a+b)+α=180°,
∴3α﹣2β=180°.
(3)当AH∥EI时,如图2所示,
过点C作MN∥AH,则MN∥AH∥EI.
∴∠CAH=∠ACM=a,∠CEI=∠ECM=b,
∴∠ACE=∠ACM+∠ECM=a+b=α,即α=a+b.
由(1)中证明可得∠ECD=∠BAC=2a,∠D=∠B=α.
在△CED中,根据三角形内角和定理有∠ECD+∠CED+∠D=180°,
即2a+2b+α=180°,
即2(a+b)=180°﹣α,
即3α=180°,解得:α=60°.
故∠B=60°.
一.选择题
1.在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是( )
A.0<AD<12 B.1<AD<6 C.0<AD<6 D.2<AD<12
2.下列不能作为判定△ABC≌△DEF的条件是( )
A.AB=DE,BC=EF,∠B=∠E B.∠A=∠D,AB=DE,∠B=∠E
C.AB=DE,BC=EF,∠A=∠D D.∠A=∠D,AC=DF,∠B=∠E
3.已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
4.如图,在△ABC中,AD垂直BC于D,BE垂直AC于E,AD、BE交于点H,且HD=DC,那么下列结论中,正确的是( )
A.AH=BD B.△AHE≌△BHD C.△ADC≌△BDH D.HE=EC
二.填空题
5.如图,△ABC的三个顶点分别在直线a、b上,且a∥b,若∠1=126°,∠2=80°,则∠3= 度.
6.在△ABC中,AB=AC,点D是△ABC外一点,连接AD、BD、CD,且BD交AC于点O,在BD上取一点E,使得AE=AD,∠EAD=∠BAC,若∠ACB=70°,则∠BDC的度数为 .
7.在△ABC中,如果AB=AC,∠A=∠C,那么△ABC的形状为 .
8.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 度.
9.若一个三角形的两边长分别是2cm和9cm,且第三边为奇数,则第三边长为 .
10.如图,在△ABC中,D在边AC上,如果AB=BD=DC,且∠C=40°,那么∠ABD= °.
11.如图,已知∠B=∠C,从下列条件中选择一个,则可以证明△OEB全等于△ODC.①AD=AE,②OB=OC,③BD=CE,④∠BEO=∠CDO,那么这个条件可以是 (写出所有符合条件的序号).
12.如图,△ABC中,AB=AC,AD是∠BAC的平分线,若△ABD的周长为16,△ABC的周长为24,则AD的长为 .
13.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件: ,使△ABC≌△FED.
14.已知△ABC中,AB=AC,∠B=50°,如果D是边BC的中点,那么∠CAD= 度.
15.如图,已知直线l1∥l2,等边三角形ABC的顶点A、C分别在直线l1、l2上,如果边AB与直线l1的夹角∠1=26°,那么边BC与直线l2的夹角∠2= 度.
16.如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 °.
三.解答题
17.如图所示,在△ABC中,AD是∠BAC的平分线,M是BC的中点,MF∥DA交BA的延长线于点E,交AC于点F,求证:BE=CF.
18.如图,△ABC中,AD⊥BC,垂足为点D,CE⊥AB,垂足为点E,AD=DC,CE和AD交于点F,联结BF,试说明∠FBD=45°.
19.如图,已知在等腰△ABC中AB=AC,点D,点E和点F分别是BC,AB和AC边上的点,且BE=DC,∠B=∠EDF,试说明DE=DF.
20.如图,在△ABC中,点D是边BC的中点,过点C作直线CE,使CE∥AB,交AD的延长线于点E.试说明AD=ED的理由.
解:因为CE∥AB(已知),
所以∠BAD= ( ).
因为点D是边BC的中点,
所以 ,
在△ABD和△ECD中,
,
所以△ABD≌△ECD( ),
所以AD=ED( ).
21.如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
22.如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
23.如图,已知AD=BC,AE=BE,说明AC=BD的理由.
24.如图,已知在△ABC中,AB=AC=BD,∠ADE=∠B,请说明△ADE是等腰三角形的理由.
25.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
26.如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,过点B作BE⊥AC,垂足为E,在线段BE上截取ED=EC,AD的延长线交BC于点P,联结DC.
(1)请说明AD=BC的理由;
(2)请说明BP=PC的理由.
27.如图,已知在△ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠ADE的度数.
28.如图,已知直线AB∥CD,∠ACD的平分线CE交AB于点F,∠AFE的平分线交CA延长线于点G.
(1)说明AC=AF的理由;
(2)若∠FCD=32°,求∠G的大小.
29.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
30.已知在△ABC与△CDE中,AB=CD,∠B=∠D,∠ACE=∠B,点B、C、D在同一直线上,射线AH、EI分别平分∠BAC、∠CED.
(1)如图1,试说明AC=CE的理由;
(2)如图2,当AH、EI交于点G时,设∠B=α,∠AGE=β,求β与α的数量关系,并说明理由;
(3)当AH∥EI时,求∠B的度数.
答案
一.选择题
1.
【分析】作出图形,延长中线AD到E,使DE=AD,利用“边角边”证明△ACD和△EBD全等,根据全等三角形对应边相等可得AC=BE,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE的范围,再除以2即可得解.
【解答】解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7﹣5<AE<7+5,
即7﹣5<2AD<7+5,
∴1<AD<6.
故选:B.
2.
【分析】根据全等三角形的判定方法判断即可.
【解答】解:A、AB=DE,BC=EF,∠B=∠E,可以利用SAS判定△ABC≌△DEF,不符合题意;
B、∠A=∠D,AB=DE,∠B=∠E,可以利用ASA判定△ABC≌△DEF,不符合题意;
C、AB=DE,BC=EF,∠A=∠D,不能利用SSA判定△ABC≌△DEF,符合题意;
D、∠A=∠D,AC=DF,∠B=∠E,可以利用AAS判定△ABC≌△DEF,不符合题意;
故选:C.
3.
【分析】根据各个选项给出的条件结合三角形内角和定理,即三角形内角和等于180°,推导出三角形中是否存在90°的内角.若存在,则△ABC是直角三角形.若不存在,则△ABC不是直角三角形.
【解答】解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
4.
【分析】首先根据垂直可得∠ADB=∠ADC=90°,然后再证明∠HAE=∠HBD,然后再利用AAS证明△ADC≌△BDH.
【解答】解:∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∴∠DAE+∠AHE=90°,
∵BE⊥AC,
∴∠HBD+∠BHD=90°,
∵∠AHE=∠BHD,
∴∠HAE=∠HBD,
在△ADC和△BDH中,
,
∴△ADC≌△BDH(AAS),
故选:C.
二.填空题
5.
【分析】根据平行线的性质及可得到答案.
【解答】解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=126°,∠2=80°,
∴∠3=∠1﹣∠2=46°,
故答案为:46.
6.
【分析】根据SAS证明△ABE≌△ACD,再利用全等三角形的性质、三角形的外角性质和三角形的内角和解答即可.
【解答】解:∵∠EAD=∠BAC,
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD (SAS),
∴∠ABD=∠ACD,
∵∠BOC是△ABO和△DCO的外角,
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC,
∴∠ABD+∠BAC=∠ACD+∠BDC,
∴∠BAC=∠BDC,
∵∠ACB=70°,AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°,
∴∠BDC=∠BAC=40°.
故答案为:40°.
7.
【分析】可利用等腰三角形的判定,说明三角形的三条边都相等,亦可利用等腰三角形的性质,说明该三角形的三个角都相等.
【解答】解:(法一)在△ABC中,∵∠A=∠C,
∴BA=BC.
又∵AB=AC,
AB=AC=BC.
所以△ABC是等边三角形.
故答案为:等边三角形.
(法二)在△ABC中,∵AB=AC,
∴∠B=∠C.
又∵∠A=∠C,
∴∠A=∠B=∠C.
所以△ABC是等边三角形.
故答案为:等边三角形.
8.
【分析】先根据对顶角的定义得出∠3的度数,再由三角形内角与外角的关系求出∠A的度数.
【解答】解:如图,
∵直线a∥b,
∴∠3=∠1,
∵∠1=56°,
∴∠3=56°,
∵∠3=∠2+∠A,∠2=29°,
∴∠A=∠3﹣∠2=56°﹣29°=27°.
故答案为:27.
9.
【分析】根据三角形的三边关系求得第三边的取值范围,再根据第三边是奇数求得第三边的长.
【解答】解:设第三边长xcm.
根据三角形的三边关系,得7<x<11.
又∵三角形的第三边长是奇数,因而满足条件的数是9cm.
故答案为:9cm.
10.
【分析】由等腰三角形的性质可得∠DBC=∠C=40°,由三角形的内角和定理可得∠BDC=180°﹣40°﹣40°=100°,由邻补角的性质可得∠ADB,易得∠A,从而求得∠ABD.
【解答】解:∵AB=BD=DC,∠C=40°,
∴∠DBC=∠C=40°,∠A=∠ADB,
∴∠BDC=180°﹣40°﹣40°=100°,
∴∠ADB=180°﹣100°=80°,
∴∠A=80°,
∴∠ABD=180°﹣∠ADB﹣∠A=180°﹣80°﹣80°=20°,
故答案为:20.
11.
【分析】根据全等三角形的判定方法解答即可.
【解答】解:选择①和②可与∠B=∠C一起得出△ABD≌△ACE(AAS),选择③可与∠B=∠C一起得出△ABD≌△ACE(AAS),
∴AB=AC,AD=AE,
∴BE=CD,
∴△OEB≌△ODC(AAS)
选择④没有已知的边,不能得到△OEB≌△ODC,
故答案为:①或②或③.
12.
【分析】先由等腰三角形三线合一的性质得出BD=CD,再根据△ABD的周长为16,得到AB+BD+AD=16,即AB+AC+BC+2AD=32,再将AB+AC+BC=24代入,即可求出AD的长.
【解答】解:∵△ABC中,AB=AC,AD是∠BAC的平分线,
∴BD=CD.
∵△ABD的周长为16,
∴AB+BD+AD=16,
∴2AB+2BD+2AD=32,
∴AB+AC+BC+2AD=32,
∵△ABC的周长为24,
∴AB+AC+BC=24,
∴24+2AD=32,
∴AD=4.
故答案为4
13.
【分析】根据三角形的判定定理:SSS、SAS、AAS进行判断即可.
【解答】解:∵AD=FC,
∴AC=FD,
∵∠A=∠F,
∴添加AB=FE,利用SAS得出△ABC≌△FED,
添加∠B=∠E,利用AAS得出△ABC≌△FED,
添加∠ACB=∠FDE,利用ASA得出△ABC≌△FED,
添加DE∥BC,得出∠EDF=∠BCA,利用ASA得出△ABC≌△FED,
故答案为:AB=FE或∠B=∠E或∠ACB=∠FDE或DE∥BC.
14.
【分析】首先利用等腰三角形的底角的度数求得另一个底角的度数,然后根据等腰三角形“三线合一”的性质求得答案即可.
【解答】解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∵D是边BC的中点,
∴AD⊥BC,
∴∠CAD=40°,
故答案为:40.
15.
【分析】由等边三角形的性质得∠BAC=∠BCA=60°,再由平行线的性质得∠1+∠BAC+∠BCA+∠2=180°,则∠1+∠2=60°,即可求解.
【解答】解:∵△ABC是等边三角形,
∴∠BAC=∠BCA=60°,
∵直线l1∥l2,
∴∠1+∠BAC+∠BCA+∠2=180°,
∴∠1+∠2=180°﹣60°﹣60°=60°,
∵∠1=26°,
∴∠2=60°﹣26°=34°,
故答案为:34.
16.
【分析】根据全等三角形的性质得出AB=AD,∠ABD=∠ADE,根据等腰三角形的性质和三角形内角和定理求出∠ABD=70°,求出∠DAE和∠ADE,再根据三角形内角和定理求出∠E即可.
【解答】解:∵△ABC≌△ADE,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠BAD=40°,
∴∠ABD=∠ADB=(180°﹣∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,
∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=114°﹣40°=74°,
∴∠E=180°﹣∠ADE﹣∠DAE=180°﹣70°﹣74°=36°,
故答案为:36.
三.解答题
17.证明:如图,过点B作BN∥AC交EM的延长线于N,
∴∠MBN=∠C,∠N=∠MFC,
∵M为BC的中点,
∴BM=CM,
在△BMN和△CMF中,
,
∴△BMN≌△CMF(AAS),
∴BN=CF,
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵ME∥AD,
∴∠E=∠BAD,∠MFC=∠CAD,
∴∠E=∠MFC,
∴∠E=∠N,
∴BE=BN,
∴BE=CF.
18.解:∵AD⊥BC,CE⊥AB,
∴∠ADC=∠ADB=90°=∠CEB,
∴∠ABD+∠BAD=90°=∠BCE+∠ABD,
∴∠BAD=∠BCE,
在△ABD和△CFD中,
,
∴△ABD≌△CFD(ASA),
∴BD=DF,
又∵∠ADB=90°,
∴∠FBD=45°.
19.解:∵AB=AC,
∴∠B=∠C,
∵∠B=∠EDF,
∴∠C=∠EDF,
∵∠EDC=∠B+∠BED=∠EDF+∠FDC,
∴∠BED=∠CDF,
在△BDE和△CFD中,
,
∴△BDE≌△CFD(ASA),
∴DE=DF.
20.解:因为CE∥AB(已知),
所以∠BAD=∠E(两直线平行,内错角相等).
因为点D是边BC的中点,
所以BD=CD,
在△ABD和△ECD中,
所以△ABD≌△ECD(AAS),
所以AD=ED(全等三角形的对应边相等).
故答案为∠E,两直线平行,内错角相等;∠BAD=∠E,对顶角相等,BD=CD;AAS;全等三角形的对应边相等.
21.解:∵AE⊥DE,
∴∠AED=90°,
又∵∠B=90°,
∴∠B=∠AED,
∵∠AEC=∠B+∠BAE,
即∠AED+∠DEC=∠B+∠BAE,
∴∠BAE=∠DEC,
在△ABE与△ECD中,
,
∴△ABE≌△ECD(ASA),
∴AE=ED,
∵EF⊥AD,
∴点F是AD的中点.
22.解:∠B与∠C相等,
理由:∵∠FDC=∠FDE+∠EDC,
又∵∠FDC=∠B+∠BFD,
∴∠FDE+∠EDC=∠B+∠BFD,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
在△BFD和△CDE中
,
∴△BFD≌△CDE(SAS),
∴∠B=∠C.
23.证明:∵AD=BC,AE=BE,
∴AD﹣AE=BC﹣BE,
即DE=CE,
在△ACE与△BDE中,
,
∴△ACE≌△BDE(SAS),
∴AC=BD.
24.解:∵AB=BD,
∴∠BAD=∠BDA,
∵∠ADE=∠B,∠ADE+∠BAD+∠AED=180°,∠B+∠BDA+∠BAD=180°,
∴∠AED=∠BAD,
∴ED=AD,
∴△ADE为等腰三角形.
25.解:AB+BE=CD,理由如下:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴AB=DE,BD=CD,
∵DE+BE=BD,
∴AB+BE=CD.
26.解:(1)∵BE⊥AC,∠BAC=45°,
∴∠ABE=90°﹣45°=45°,
∴BE=AE,
在△BCE和△ADE中,
,
∴△BCE≌△ADE(SAS),
∴AD=BC.
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵BE⊥AC,BE=AE,EC=ED,
∴∠DCE=∠CDE=∠EBA=∠BAE=45°,
∴∠ABC﹣∠EBA=∠ACB﹣∠DCE,即∠DBC=∠DCB,
∴BD=CD,
∴PD为线段BC的垂直平分线,
∴BP=PC.
27.解:∵AB=AC,∠BAC=80°,AD⊥BC,
∴∠BAD=∠CAD=∠BAC=40°,
∵AD=AB,
∴∠BDA=×(180°﹣40°)=70°,
∴∠ADE=180°﹣∠BDA=180°﹣70°=110°.
28.(1)证明:∵∠ACD的平分线CE交AB于点F,
∴∠ACF=∠DCF,
∵AB∥CD,
∴∠AFC=∠DCF,
∴∠ACF=∠AFC,
∴AC=AF;
(2)解:∵∠FCD=32°,AB∥CD,
∴∠ACD=∠GAF=64°,∠AFC=32°,
∵∠AFE的平分线交CA延长线于点G.
∴∠AFG=∠GFE=AFE=,
∴∠G=180°﹣∠GAF﹣∠AFG=180°﹣64°﹣74°=42°.
29.解:(1)AD=CB,理由如下:
∵AD∥BC,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,理由如下:
∵AD=CB,BE=AD,
∴BC=BE,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(ASA),
∴FB=DB.
30.(1)证明:∵∠ACD=∠ACE+∠ECD=∠A+∠B,
又∠B=∠ACE,
∴∠A=∠ECD.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA).
∴AC=CE.
(2)解:3α﹣2β=180°.理由如下:
如图1所示,连接GC并延长至点K.
∵AH、EI分别平分∠BAC、∠DEC,
则设∠CAH=∠BAH=a,∠CEI=∠DEI=b,
∵∠ACK为△ACG的外角,
∴∠ACK=a+∠AGC,
同理可得∠ECK=b+∠EGC,
∴∠ACE=∠ACK+∠ECK=∠B=α
=(a+∠AGC)+(b+∠EGC)=a+b+∠AGE=a+b+β,
即α=a+b+β,
∴a+b=α﹣β.
又由(1)中证明可知∠ECD=∠BAC=2a,
由三角形内角和公式可得∠ECD+∠DEC+∠D=180°,
即2a+2b+α=180°,
∴2(a+b)+α=180°,
∴3α﹣2β=180°.
(3)当AH∥EI时,如图2所示,
过点C作MN∥AH,则MN∥AH∥EI.
∴∠CAH=∠ACM=a,∠CEI=∠ECM=b,
∴∠ACE=∠ACM+∠ECM=a+b=α,即α=a+b.
由(1)中证明可得∠ECD=∠BAC=2a,∠D=∠B=α.
在△CED中,根据三角形内角和定理有∠ECD+∠CED+∠D=180°,
即2a+2b+α=180°,
即2(a+b)=180°﹣α,
即3α=180°,解得:α=60°.
故∠B=60°.
