数学:1.1.1《两个基本计数原理》课件(新人教版a选修2-3)
文档属性
| 名称 | 数学:1.1.1《两个基本计数原理》课件(新人教版a选修2-3) |  | |
| 格式 | rar | ||
| 文件大小 | 330.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 05:29:00 | ||
图片预览





文档简介
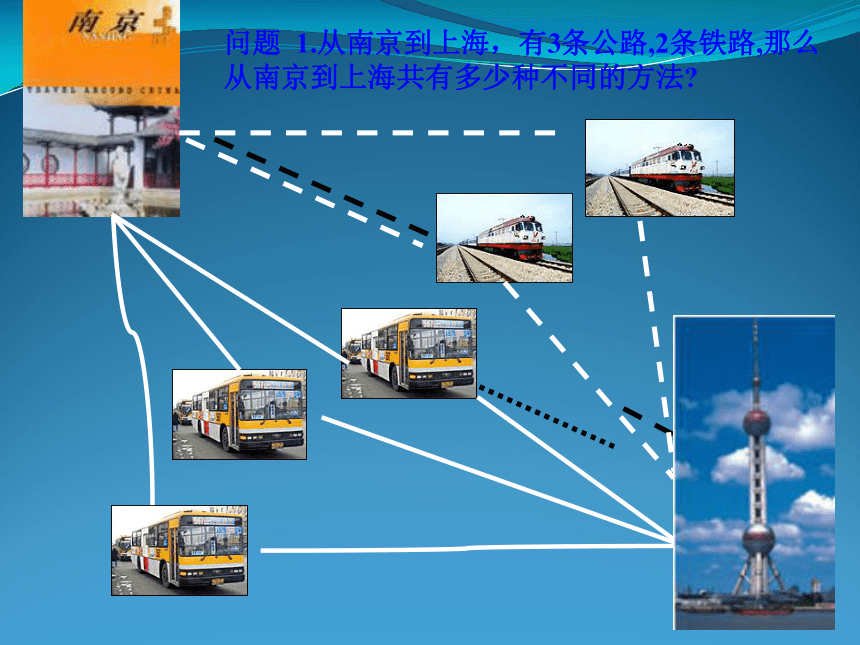
课件15张PPT。2019/3/13两个基本计数原理2019/3/13问题情境1:2019/3/13问题 1.从南京到上海,有3条公路,2条铁路,那么从南京到上海共有多少种不同的方法?上海宁波2019/3/13问题2、增加杭州游,从南京到杭州的路有三条,由杭州到上海的路有两条。问:从南京经杭州到上海有多少种不同的方法?上海宁波杭州2019/3/13
完成一件事, 有n类方式, 在第一类方式,中有m1种不同的方法,在第二类方式,中有m2种不同的方法,……,在第n类方式,中有mn种不同的方法. 那么完成这件事共有
种不同的方法。
完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有
N=m1×m2×…×mn
种不同的方法。
注:本原理又称加法原理.注:本原理又称乘法原理.分步计数原理分类计数原理N=m1+m2+…+m n2019/3/13例1: 某班共有男生28名,女生20名,从该班选出学生代表参加校学代会.
若学校分配给该班1名代表,有多少种不同的选法?
若学校分配给该班2名代表,且男女生代表各1名,有多少种不同的选法?
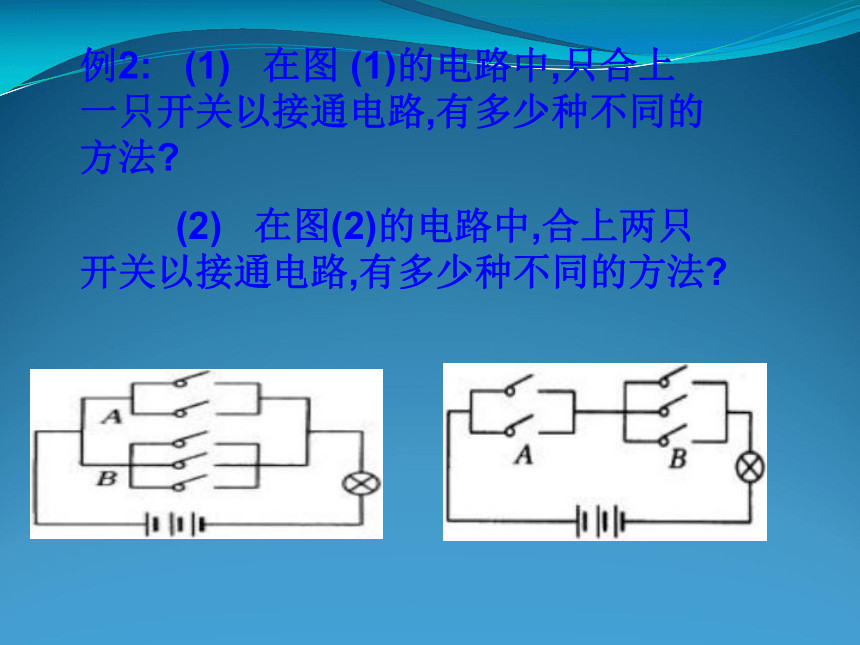
2019/3/13例2: (1) 在图 (1)的电路中,只合上一只开关以接通电路,有多少种不同的方法?
(2) 在图(2)的电路中,合上两只开关以接通电路,有多少种不同的方法?2019/3/13(1) 在图 (1)的电路中,只合上一只开关以接通电路,有多少种不同的方法?
在图(1)中按要求接通电路,只要在A中的两个开关或B中的三个开关中合上一只即可,故有
2+3=5
种不同的方法.2019/3/13(2) 在图(2)的电路中,合上两只开关以接通电路,有多少种不同的方法?在图(2)中,按要求接通电路必须分两步进行:第一步,合上A中的一只开关;第二步,合上B中的一只开关。故有
2×3=6 种不同方法。
答:在图 (1)的电路中,只合上一只开关以接通电路,有5种不同的方法;图(2)的电路中,合上两只开关以接通电路,有6种不同的方法.2019/3/13………...ABABm1m1m2m2mnmn2019/3/13例3:为了确保电子信箱的安全,在注册时通常要设置电子信箱密码.在网站设置的信箱中,
密码为4位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
密码为4位,每位是0到9这10个数字中的一个,或是从A到Z这26个英文字母中的1个,这样的密码共有多少个?
3) 密码为4~6位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
2019/3/13密码为4位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
解:(1) 设置四位密码,每一位上都可以从0到9这10个数字中取一个,有10种取法,根据分步计数原理,四位密码的个数是
10×10×10×10=100002019/3/13密码为4位,每位是0到9这10个数字中的一个,或是从A到Z这26个英文字母中的1个,这样的密码共有多少个?
(2)设置四位密码,每一位上都可以从0到9这10个数字或从A到Z这26个英文字母中的1个中取一个,共有10+26=36种取法.
根据分步计数原理,四位密码的个数是
36×36×36×36=1679616
2019/3/133) 密码为4~6位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
(3)设置一个由0到9这10个数字组成的4~6位密码,有3类方式,其中设置4位密码 、5位密码、6位密码的个数 分别为104,105,106,根据分类计数原理,设置由0到9这10个数字组成的4~6位密码个数是
104+105+106=11100002019/3/13课堂小结1. 分类计数与分步计数原理是两个最基本,也是最重要的原理,是解答排列、组合问题,尤其是较复杂的排列、组合问题的基础.
2.辨别运用分类计数原理还是分步计数原理的关键是“分类”还是“分步”,也就是说“分类”时,各类办法中的每一种方法都是独立的,都能直接完成这件事,而“分步”时,各步中的方法是相关的,缺一不可,当且仅当做完个步骤时,才能完成这件事.课堂小结
完成一件事, 有n类方式, 在第一类方式,中有m1种不同的方法,在第二类方式,中有m2种不同的方法,……,在第n类方式,中有mn种不同的方法. 那么完成这件事共有
种不同的方法。
完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有
N=m1×m2×…×mn
种不同的方法。
注:本原理又称加法原理.注:本原理又称乘法原理.分步计数原理分类计数原理N=m1+m2+…+m n2019/3/13例1: 某班共有男生28名,女生20名,从该班选出学生代表参加校学代会.
若学校分配给该班1名代表,有多少种不同的选法?
若学校分配给该班2名代表,且男女生代表各1名,有多少种不同的选法?
2019/3/13例2: (1) 在图 (1)的电路中,只合上一只开关以接通电路,有多少种不同的方法?
(2) 在图(2)的电路中,合上两只开关以接通电路,有多少种不同的方法?2019/3/13(1) 在图 (1)的电路中,只合上一只开关以接通电路,有多少种不同的方法?
在图(1)中按要求接通电路,只要在A中的两个开关或B中的三个开关中合上一只即可,故有
2+3=5
种不同的方法.2019/3/13(2) 在图(2)的电路中,合上两只开关以接通电路,有多少种不同的方法?在图(2)中,按要求接通电路必须分两步进行:第一步,合上A中的一只开关;第二步,合上B中的一只开关。故有
2×3=6 种不同方法。
答:在图 (1)的电路中,只合上一只开关以接通电路,有5种不同的方法;图(2)的电路中,合上两只开关以接通电路,有6种不同的方法.2019/3/13………...ABABm1m1m2m2mnmn2019/3/13例3:为了确保电子信箱的安全,在注册时通常要设置电子信箱密码.在网站设置的信箱中,
密码为4位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
密码为4位,每位是0到9这10个数字中的一个,或是从A到Z这26个英文字母中的1个,这样的密码共有多少个?
3) 密码为4~6位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
2019/3/13密码为4位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
解:(1) 设置四位密码,每一位上都可以从0到9这10个数字中取一个,有10种取法,根据分步计数原理,四位密码的个数是
10×10×10×10=100002019/3/13密码为4位,每位是0到9这10个数字中的一个,或是从A到Z这26个英文字母中的1个,这样的密码共有多少个?
(2)设置四位密码,每一位上都可以从0到9这10个数字或从A到Z这26个英文字母中的1个中取一个,共有10+26=36种取法.
根据分步计数原理,四位密码的个数是
36×36×36×36=1679616
2019/3/133) 密码为4~6位,每位均为0到9这10个数字中的一个数字,这样的 密码共有多少个?
(3)设置一个由0到9这10个数字组成的4~6位密码,有3类方式,其中设置4位密码 、5位密码、6位密码的个数 分别为104,105,106,根据分类计数原理,设置由0到9这10个数字组成的4~6位密码个数是
104+105+106=11100002019/3/13课堂小结1. 分类计数与分步计数原理是两个最基本,也是最重要的原理,是解答排列、组合问题,尤其是较复杂的排列、组合问题的基础.
2.辨别运用分类计数原理还是分步计数原理的关键是“分类”还是“分步”,也就是说“分类”时,各类办法中的每一种方法都是独立的,都能直接完成这件事,而“分步”时,各步中的方法是相关的,缺一不可,当且仅当做完个步骤时,才能完成这件事.课堂小结
