数学:2.4.3《二次函数的最值问题》课件(北师大版必修1)
文档属性
| 名称 | 数学:2.4.3《二次函数的最值问题》课件(北师大版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 904.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 00:00:00 | ||
图片预览


文档简介
课件18张PPT。二次函数的最值2019-3-13二次函数的最值问题重点 掌握闭区间上的二函数的
最值问题难点 了解并会处理含参数的二
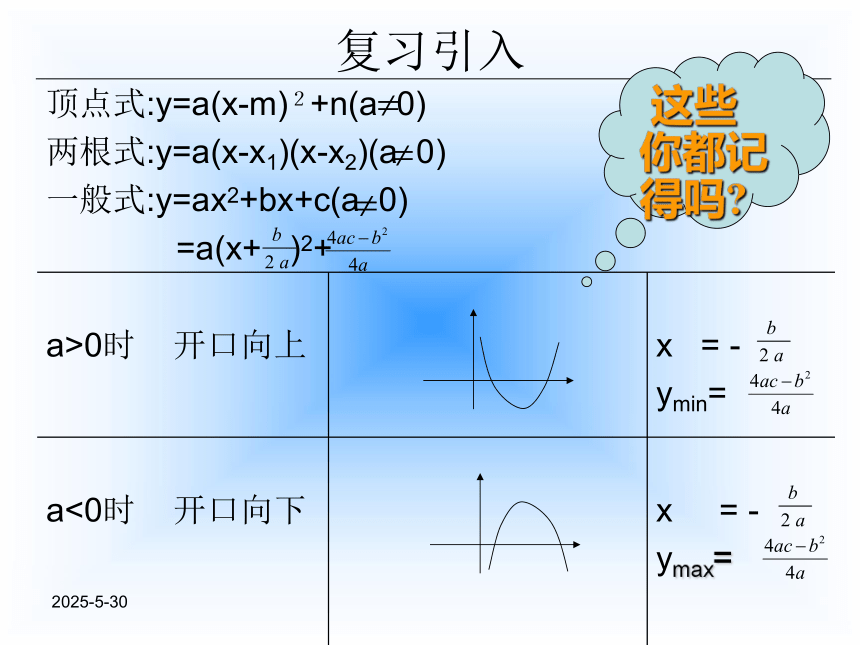
次函数的最值问题核心 区间与对称轴的相对位置思想 数形结合 分类讨论 2019-3-13复习引入 这些你都记得吗?2019-3-13 新 课一、闭区间上的二次函数的最值
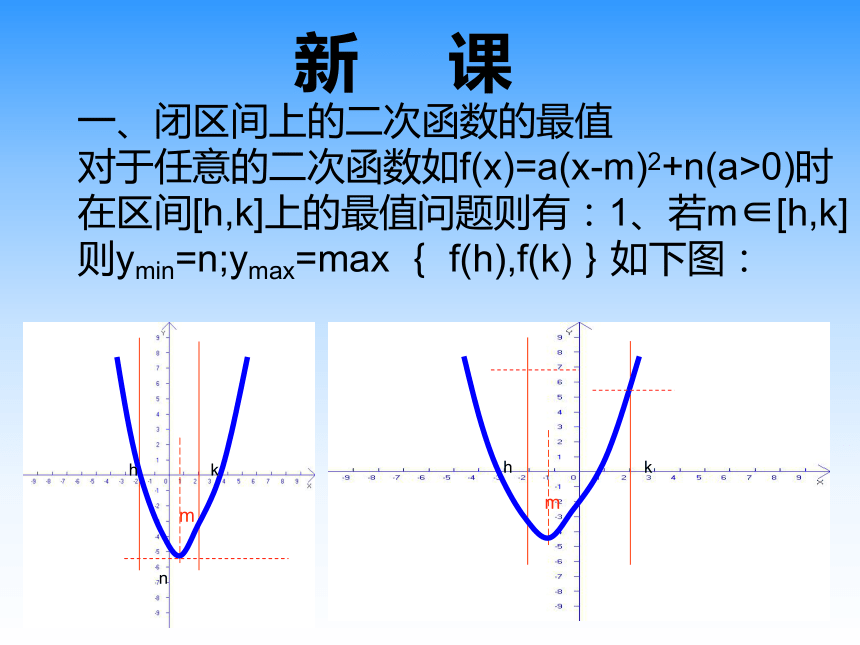
对于任意的二次函数如f(x)=a(x-m)2+n(a>0)时
在区间[h,k]上的最值问题则有:1、若m∈[h,k]
则ymin=n;ymax=max { f(h),f(k)}如下图:
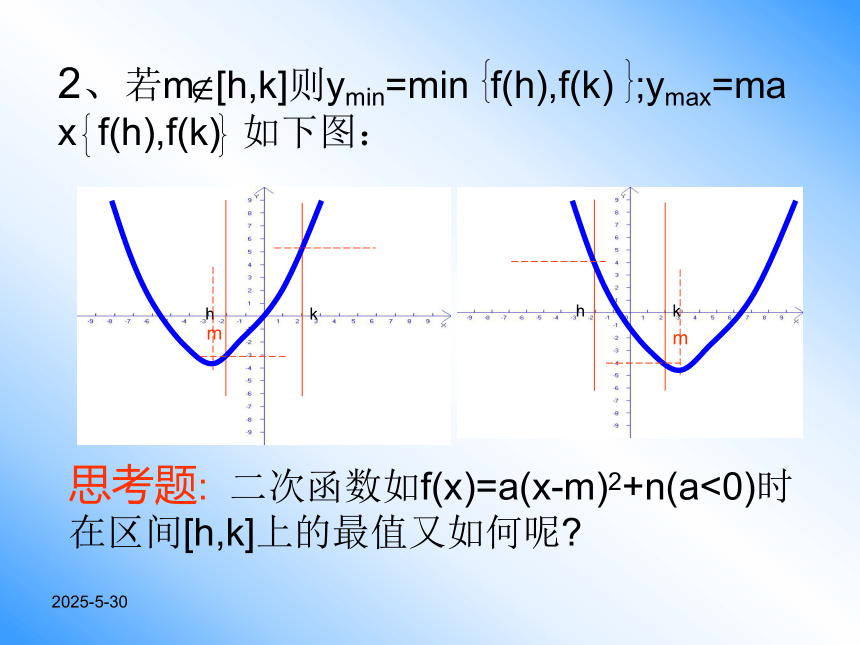
2019-3-13思考题: 二次函数如f(x)=a(x-m)2+n(a<0)时
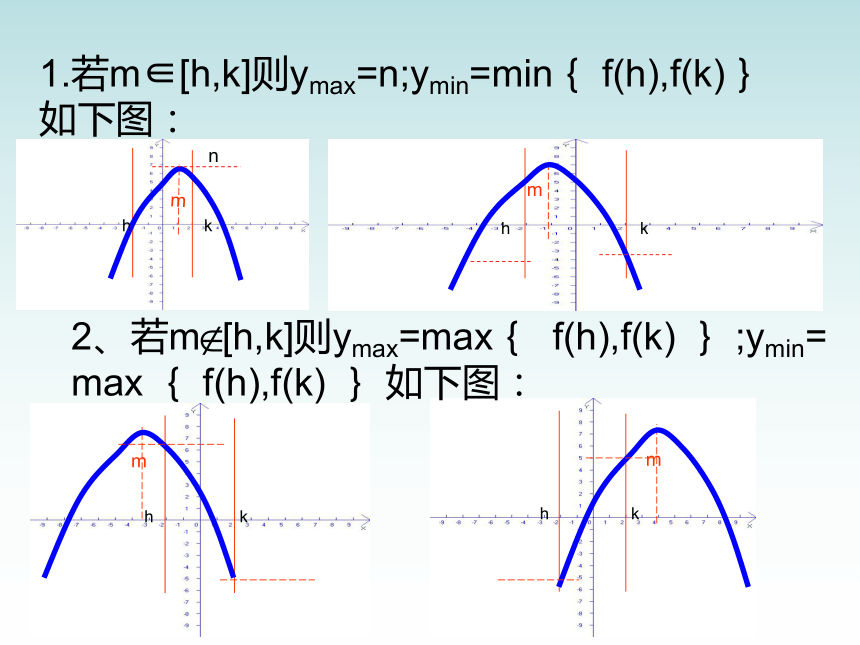
在区间[h,k]上的最值又如何呢?2019-3-131.若m∈[h,k]则ymax=n;ymin=min{ f(h),f(k)}
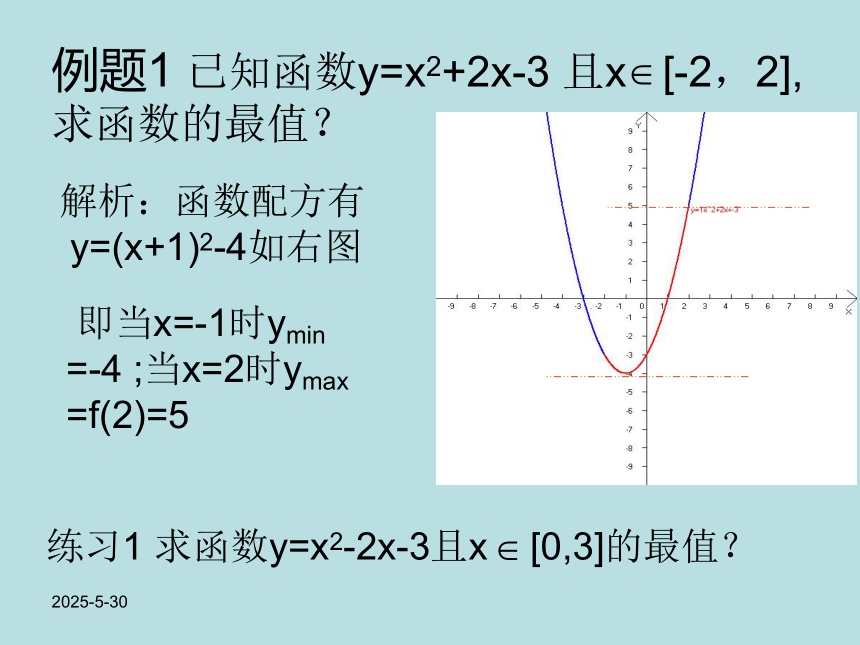
如下图:n2019-3-13 即当x=-1时ymin
=-4 ;当x=2时ymax
=f(2)=5解析:函数配方有
y=(x+1)2-4如右图2019-3-13解析:y= -x2-2x+3
= -(x+1)2+4
2019-3-13二、含参变量的二次函数最值问题
解析:因为函数y=x2+2ax+3 =(x+a)2+3-a2
的对称轴为x=-a。要求最值则要看x=-a
是否在区间[-2,2]之内,则从以下几个
方面解决如图:1、轴动区间静 2、轴静区间动
2019-3-132019-3-13 Ⅱ 当-2<-a≤0时 f(x) max=f(2)=7+4a
(0≤a < 2) f(x) min=f(-a)=3-a2
Ⅰ 当-a≤-2 时 f(x) max= f(2)=7+4a
(a≥2) 时 f(x) min=f(-2)=7-4a
Ⅲ 当0<-a≤2时 f(x) max=f(-2)=7-4a
(-2 ≤a <0) f(x) min=f(-a)=3-a2
Ⅳ 当 -a>2 时 f(x) max=f(-2)=7-4a
(a ≤ -2) f(x) min=f(2)=7+4a 则由上图知解为:2019-3-13 例4 求函数y=x2-2x-3在x∈[k,k+2]的
函数的最值?解析: 因为函数 y=x2-2x-3=(x-1)2-4的对称
轴为 x=1 固定不变,要求函数的最值,
即要看区间[k,k+2]与对称轴 x=1的位
置,则从以下几个方面解决如图:2019-3-13X=12019-3-13则由上图知解为: 当k+2≤1(k ≤-1)时 f(x)max=f(k)=k2-2k-3
f(x)min=f(k+2)=k2+2k+3 当 k <1 < k+2 时 f(x)max=max{f(k),f(k+2)}
(-1 <k <1) f(x)min=f(1)=-4 当k ≥1 时 f(x) max=f(k+2)=k2+2k+3
f(x) min=f(k)=k2-2k-3
2019-3-13例5 求函数y=x2-2x-3在x∈[-3,m]函数的最值?
解析:因为函数 y=x2-2x-3=(x-1)2-4 的对称轴为x=1 固定不变,要求函数的最值, 即要根据具体的区间 [-3,m] 与对称轴x=1的位置,则从以下两个方面解决如图:2019-3-13m2019-3-13则由上图知解为:Ⅰ当-3<m≤1时 f(x)max=f(-3)=12
f(x)min=f(m)=m2+2m+3
Ⅱ当 1<m 时 f(x)max=max{f(-3),f(m)}
f(x)min=f(1)=-4
练习3 求函数y=x2-2ax-3在x∈[0,3]的最值?
练习4 求函数y=x2+2x-3在x∈[m,3]的最值?
2019-3-13课堂小结2019-3-13
最值问题难点 了解并会处理含参数的二
次函数的最值问题核心 区间与对称轴的相对位置思想 数形结合 分类讨论 2019-3-13复习引入 这些你都记得吗?2019-3-13 新 课一、闭区间上的二次函数的最值
对于任意的二次函数如f(x)=a(x-m)2+n(a>0)时
在区间[h,k]上的最值问题则有:1、若m∈[h,k]
则ymin=n;ymax=max { f(h),f(k)}如下图:
2019-3-13思考题: 二次函数如f(x)=a(x-m)2+n(a<0)时
在区间[h,k]上的最值又如何呢?2019-3-131.若m∈[h,k]则ymax=n;ymin=min{ f(h),f(k)}
如下图:n2019-3-13 即当x=-1时ymin
=-4 ;当x=2时ymax
=f(2)=5解析:函数配方有
y=(x+1)2-4如右图2019-3-13解析:y= -x2-2x+3
= -(x+1)2+4
2019-3-13二、含参变量的二次函数最值问题
解析:因为函数y=x2+2ax+3 =(x+a)2+3-a2
的对称轴为x=-a。要求最值则要看x=-a
是否在区间[-2,2]之内,则从以下几个
方面解决如图:1、轴动区间静 2、轴静区间动
2019-3-132019-3-13 Ⅱ 当-2<-a≤0时 f(x) max=f(2)=7+4a
(0≤a < 2) f(x) min=f(-a)=3-a2
Ⅰ 当-a≤-2 时 f(x) max= f(2)=7+4a
(a≥2) 时 f(x) min=f(-2)=7-4a
Ⅲ 当0<-a≤2时 f(x) max=f(-2)=7-4a
(-2 ≤a <0) f(x) min=f(-a)=3-a2
Ⅳ 当 -a>2 时 f(x) max=f(-2)=7-4a
(a ≤ -2) f(x) min=f(2)=7+4a 则由上图知解为:2019-3-13 例4 求函数y=x2-2x-3在x∈[k,k+2]的
函数的最值?解析: 因为函数 y=x2-2x-3=(x-1)2-4的对称
轴为 x=1 固定不变,要求函数的最值,
即要看区间[k,k+2]与对称轴 x=1的位
置,则从以下几个方面解决如图:2019-3-13X=12019-3-13则由上图知解为: 当k+2≤1(k ≤-1)时 f(x)max=f(k)=k2-2k-3
f(x)min=f(k+2)=k2+2k+3 当 k <1 < k+2 时 f(x)max=max{f(k),f(k+2)}
(-1 <k <1) f(x)min=f(1)=-4 当k ≥1 时 f(x) max=f(k+2)=k2+2k+3
f(x) min=f(k)=k2-2k-3
2019-3-13例5 求函数y=x2-2x-3在x∈[-3,m]函数的最值?
解析:因为函数 y=x2-2x-3=(x-1)2-4 的对称轴为x=1 固定不变,要求函数的最值, 即要根据具体的区间 [-3,m] 与对称轴x=1的位置,则从以下两个方面解决如图:2019-3-13m2019-3-13则由上图知解为:Ⅰ当-3<m≤1时 f(x)max=f(-3)=12
f(x)min=f(m)=m2+2m+3
Ⅱ当 1<m 时 f(x)max=max{f(-3),f(m)}
f(x)min=f(1)=-4
练习3 求函数y=x2-2ax-3在x∈[0,3]的最值?
练习4 求函数y=x2+2x-3在x∈[m,3]的最值?
2019-3-13课堂小结2019-3-13
