数学:3.2.2《指数扩充及其运算性质》课件(北师大版必修1)
文档属性
| 名称 | 数学:3.2.2《指数扩充及其运算性质》课件(北师大版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 903.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 05:37:00 | ||
图片预览







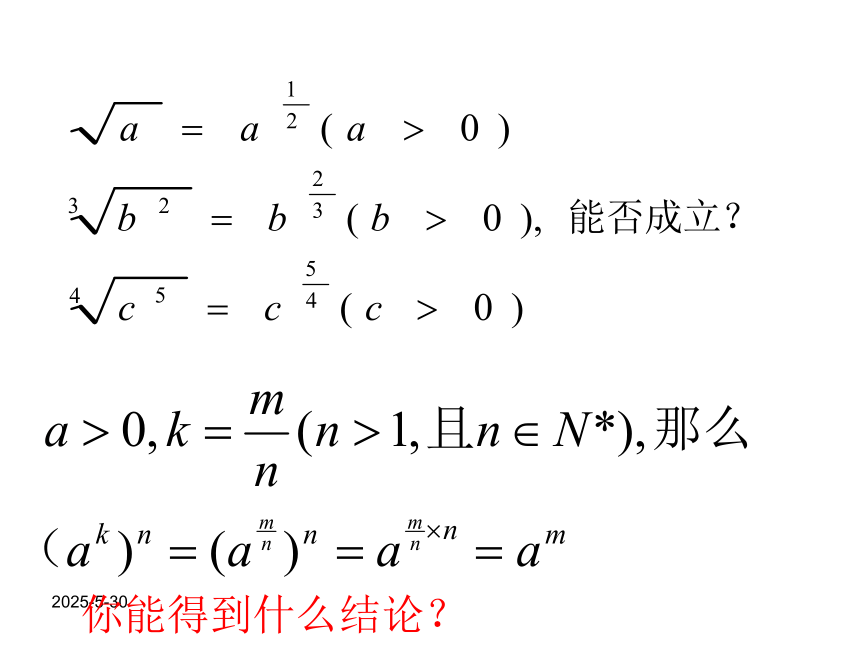
文档简介
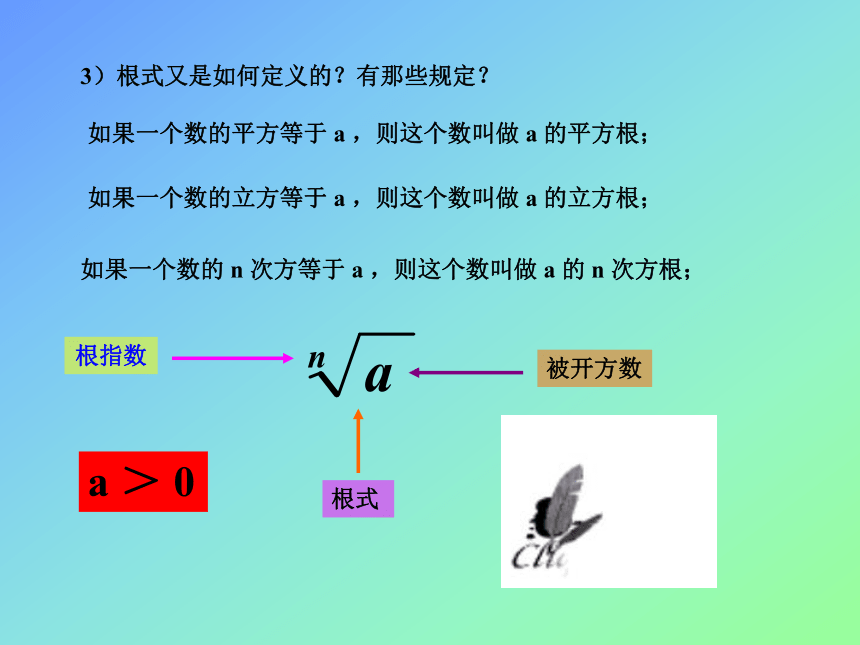
课件22张PPT。2019/3/13§3.2.2指数扩充及其运算性质1)整数指数幂是如何定义的?有何规定?a 0 = 1 ( a ≠ 0 )2019/3/132)整数指数幂有那些运算性质? ( m、n ∈Z )(1)a m ×a n = a m + n(2)( a m ) n = a m × n(3)( a b ) n = a m b na m ÷a n = a m ×b -n = a m-n= ( a ×b -1 ) n = a n × b -n3)根式又是如何定义的?有那些规定?如果一个数的平方等于 a ,则这个数叫做 a 的平方根;如果一个数的立方等于 a ,则这个数叫做 a 的立方根;如果一个数的 n 次方等于 a ,则这个数叫做 a 的 n 次方根;a > 04) 的运算结果如何?当 n 为奇数时, = a ; ( a ∈ R ) 2019/3/13一,引入:1, 的5次方根是________
2, a12的3次方根是___________你发现了什么?1。2。2019/3/132019/3/13你能得到什么结论?2019/3/13规定? 正数的正分数指数幂
(3)0的正分数 指数幂等于0, 0的负分数 指数幂没有意义。
二,分数指数幂的定义例1、 用分数指数幂的形式表示下列各式:
(式中a>0) 解: 2019/3/13题型一将根式转化分数指数幂的形式。(a>0,b>0)小结:1,当有多重根式是,要由里向外层层转化。
2、对于有分母的,可以先把分母写成负指数幂。
3、要熟悉运算性质。【课堂练习】第1题:【课堂练习】第2题:(a+b>0) (1)(2)(3)(4)(5)(6)分数指数幂的运算性质:
整数指数幂的运算性质可以运用到分数指数幂,进而推广到有理数范围:
例3 求值: = 2019/3/13题型二分数指数幂 求值,先把a写成 然后原式便化为
(即:关键先求a的n次方根)【课堂练习】2.用分数指数幂表示下列各式: 【课堂练习】3、用分数指数幂表示下列各式: 2019/3/13条件求值证明问题
例2 已知 ,求下列各式的值
(1) (2) 练习(变式)设 的值。 小结 1、分数指数幂的概念(与整数指数幂对比,有何 差异,注意不能随意约分). 2、分数指数幂的运算性质,进而推广到有理数指数幂的运算性质。 3、根式运算时,先化为指数形式进行运算,原式为根式的,再将结果化为根式。
注意三点:
1. 课本P68-69习题3-2
A 3. 4. 6. B 4
作业:
2, a12的3次方根是___________你发现了什么?1。2。2019/3/132019/3/13你能得到什么结论?2019/3/13规定? 正数的正分数指数幂
(3)0的正分数 指数幂等于0, 0的负分数 指数幂没有意义。
二,分数指数幂的定义例1、 用分数指数幂的形式表示下列各式:
(式中a>0) 解: 2019/3/13题型一将根式转化分数指数幂的形式。(a>0,b>0)小结:1,当有多重根式是,要由里向外层层转化。
2、对于有分母的,可以先把分母写成负指数幂。
3、要熟悉运算性质。【课堂练习】第1题:【课堂练习】第2题:(a+b>0) (1)(2)(3)(4)(5)(6)分数指数幂的运算性质:
整数指数幂的运算性质可以运用到分数指数幂,进而推广到有理数范围:
例3 求值: = 2019/3/13题型二分数指数幂 求值,先把a写成 然后原式便化为
(即:关键先求a的n次方根)【课堂练习】2.用分数指数幂表示下列各式: 【课堂练习】3、用分数指数幂表示下列各式: 2019/3/13条件求值证明问题
例2 已知 ,求下列各式的值
(1) (2) 练习(变式)设 的值。 小结 1、分数指数幂的概念(与整数指数幂对比,有何 差异,注意不能随意约分). 2、分数指数幂的运算性质,进而推广到有理数指数幂的运算性质。 3、根式运算时,先化为指数形式进行运算,原式为根式的,再将结果化为根式。
注意三点:
1. 课本P68-69习题3-2
A 3. 4. 6. B 4
作业:
