数学:3.3.1《指数函数》课件(北师大版必修1)
文档属性
| 名称 | 数学:3.3.1《指数函数》课件(北师大版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 342.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 05:38:00 | ||
图片预览




文档简介
课件14张PPT。2019/3/13少 小 不 学 习,老 来 徒 伤 悲 成功=艰苦的劳动+正确的方法+少谈空话天才就是百分之一的灵感,百分之九十九的汗水!天 才 在 于 勤 奋,努 力 才 能 成 功!2019年3月13日星期三 知 识 改 变 命 运,勤 奋 创 造 奇 迹.§3.3.1指数函数2019/3/13某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……1个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系是在这个函数里,自变量x 作为指数,而底数2是一个大于0且不等于1的常量.2019/3/132019/3/131、指数函数的定义一般地,函数y=a x (a>0,且a≠1)叫做指数函数,其中x是自变量.函数的定义域是R .问: ① y= - 4 x ,y=x 4 , y=(-2) x 是指数函数吗?问: ②为什么规定底数a大于0且不等于1 ?如果a=0 那么当x>0时,a x =0,当x≤0时, a x 无意义
如果a<0 如y=( - 4) x 这时对于x= 等,在实数范围内函数值不存在.
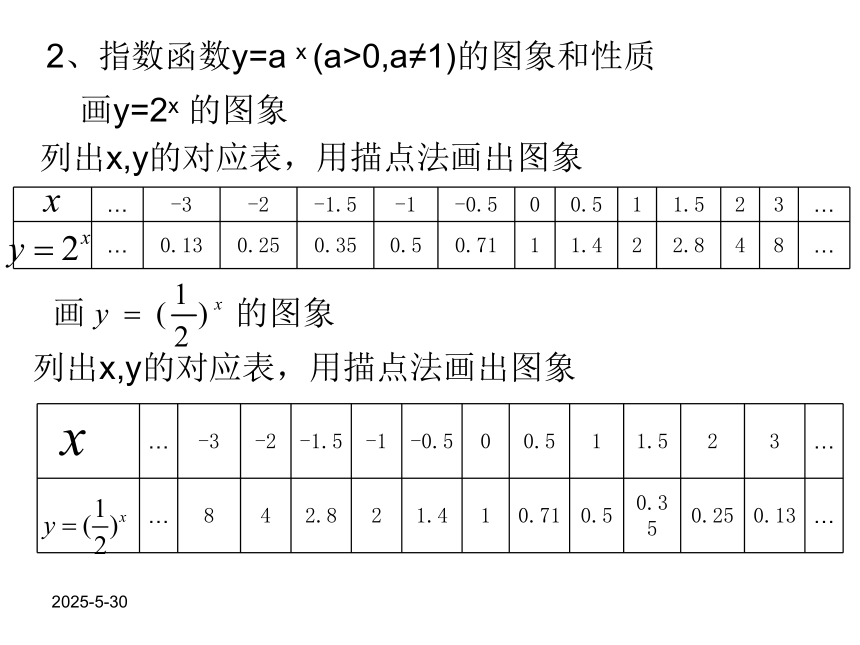
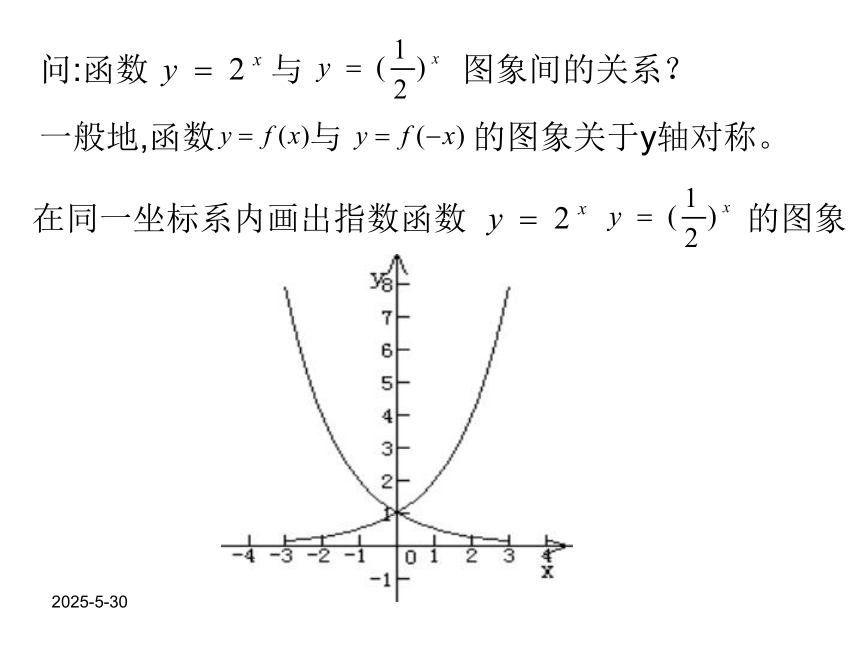
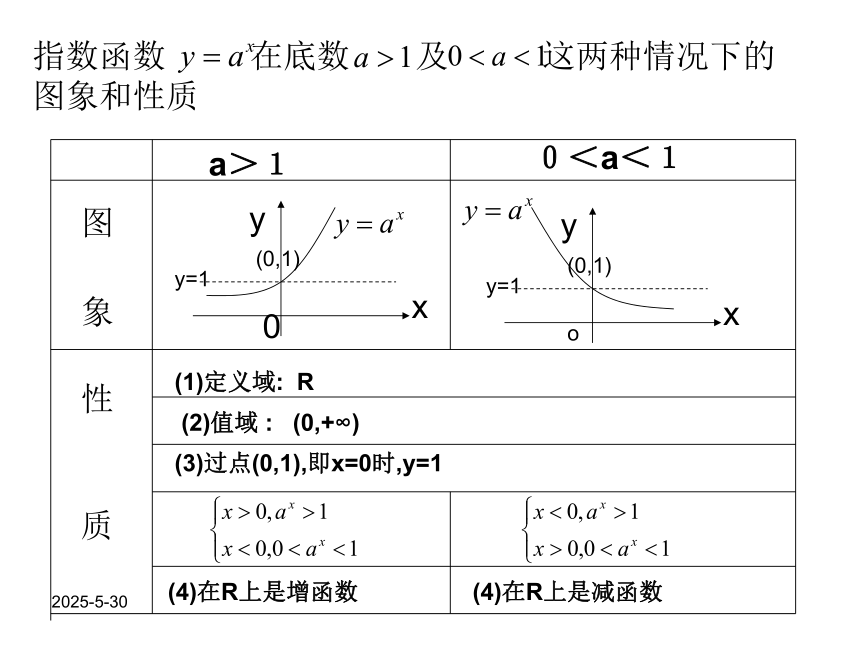
如果a=1 这时y=1x =1是一个常量,对它没有研究的必要为了避免上述各种情况,所以规定a>0,且a≠1即a>1或00,a≠1)的图象和性质画y=2x 的图象列出x,y的对应表,用描点法画出图象 列出x,y的对应表,用描点法画出图象 2019/3/13问:函数 与 图象间的关系?一般地,函数 与 的图象关于y轴对称。 在同一坐标系内画出指数函数 的图象2019/3/13指数函数 在底数 及 这两种情况下的图象和性质 a>10<a<1图 象性 质(1)定义域: R(2)值域 : (0,+∞)(3)过点(0,1),即x=0时,y=1(4)在R上是增函数(4)在R上是减函数2019/3/133、例题分析例1.某种放射性物质不断变化为其他物质,每经过1年剩留的这种物质是原来的84%,画出这种物质的剩留量随时间变化的图象,并从图象上求出经过多少年,剩量留是原来的一半(结果保留1个有效数字)。分析:通过恰当假设,将剩留量y表示成经过年数x的函数,并可列表、描点、作图,进而求得所求。解:设这种物质量初的质量是1,经过x年,剩留量是y 经过1年,剩留量=1×84%=0.841;经过2年,剩留量=1×84%=0.842;……一般地,经过x年,剩留量2019/3/13根据这个函数关系式可以列表如下 用描点法画出指数函数 的图象。从图上看出 ,只需答:约经过4年,剩留量是原来的一半。2019/3/13例2、说明下列函数的图象与指数函数 的图象的关系,并画出它们的示意图: (1)(2)解:(1)比较函数 与 的关系: 与 相等, 与 相等, 与 相等, 由此可以知道,将指数函数 的图象向左平移1个单位长度,就得到函数 的图象。2019/3/13说明:一般地,当时a>0时,将函数y=f(x)的图象向左平移a个单位得到y=f(x+a)的图象;
当时a<0时,将函数y=f(x)的图象向右平移|a|个单位得到的y=f(x+a)图象;2019/3/13例3:比较下列各题中两个值的大小:
(1) 1.72.5, 1.73;
(2) 0.8-0.1, 0.8-0.2;
(3) 1.70.3, 0.93.1.对上述解题过程,可总结出比较同底数幂大小的方法,即用指数函数的单调性,其基本步骤如下:
(1)确定所要考查的指数函数;
(2)根据底数情况指出已确定的指数函数的单调性;
(3)比较指数大小,然后利用指数函数单调性得出同底数幂的大小关系。
(4)对于不同底不同指数的函数值比较大小,一般要找中间量.2019/3/13作 业P76: T1, T32019/3/13再见
如果a<0 如y=( - 4) x 这时对于x= 等,在实数范围内函数值不存在.
如果a=1 这时y=1x =1是一个常量,对它没有研究的必要为了避免上述各种情况,所以规定a>0,且a≠1即a>1或0
当时a<0时,将函数y=f(x)的图象向右平移|a|个单位得到的y=f(x+a)图象;2019/3/13例3:比较下列各题中两个值的大小:
(1) 1.72.5, 1.73;
(2) 0.8-0.1, 0.8-0.2;
(3) 1.70.3, 0.93.1.对上述解题过程,可总结出比较同底数幂大小的方法,即用指数函数的单调性,其基本步骤如下:
(1)确定所要考查的指数函数;
(2)根据底数情况指出已确定的指数函数的单调性;
(3)比较指数大小,然后利用指数函数单调性得出同底数幂的大小关系。
(4)对于不同底不同指数的函数值比较大小,一般要找中间量.2019/3/13作 业P76: T1, T32019/3/13再见
