北京市北京第二外国语学院附属中学2023-2024学年高一下学期期中考试数学试卷(PDF版无答案)
文档属性
| 名称 | 北京市北京第二外国语学院附属中学2023-2024学年高一下学期期中考试数学试卷(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 10:44:07 | ||
图片预览

文档简介
2023-2024学年第二学期期中质量检测
2024年5月8日
高一数学
(北京第二外国语学院附属中学)
:·本试卷共4页,150分。考试时长120分钟。
第I卷(选择题共50分)
.一、选择题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项。
.15已知向量ā=0,-2),6=(x,4),且aii.,则a-=()
A.55
B.2√2
C.25
D.3W5
2.i是虚数单位,若复数(1-2i)(a+i)是纯虚数,则实数a的值为(、
A.2
B.-2
c.
D月
3,己知一个圆锥和圆柱的底面半径和高分别相等,若圆锥的轴截面是等边三角形,则这个圆锥和圆柱的
侧面积之比为()
A:克
B.2
C.
3
D.万
4.已知向量à=(2,4),6=(3,-1),则“k=√5"是“(a+k)1(a-k的()
A.充分不必要条件
B,必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
5.在aABC中,角A,B,C的对边分别为a,b,c,若a=2 bcosC,则△ABC一定是()
A,正三角形
B.直角三角形
C.等腰或直角三角形D.等腰三角形
6.如图,在正方体ABCD-ABCD中,点P是线段AC上的动点,下列与BP始终异面的是()
0
A.DD,
B.AC
C.AD
D.BC
7.已知两条直线m,n和平面a,那么下列命题中的真命题是()
A.若m⊥n,nca,则m⊥a
B.若m⊥n,n⊥a,则m/1a
C.若m⊥a,nca,则m⊥n
D.若m/la,n/1a,则m∥n
8.一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶4h后,船到达C处,
看到这个灯塔在北偏东15°,这时船与灯塔的距离为()
第1页共4页
A.30v2 km
B.306 km
C.156km
D.15√5km
9,已知正方形ABCD的边长为1,点P是对角线BD上任意一点,则P.BD的取值范围为()
a【
B
22
c.【l,
D.[-2
9
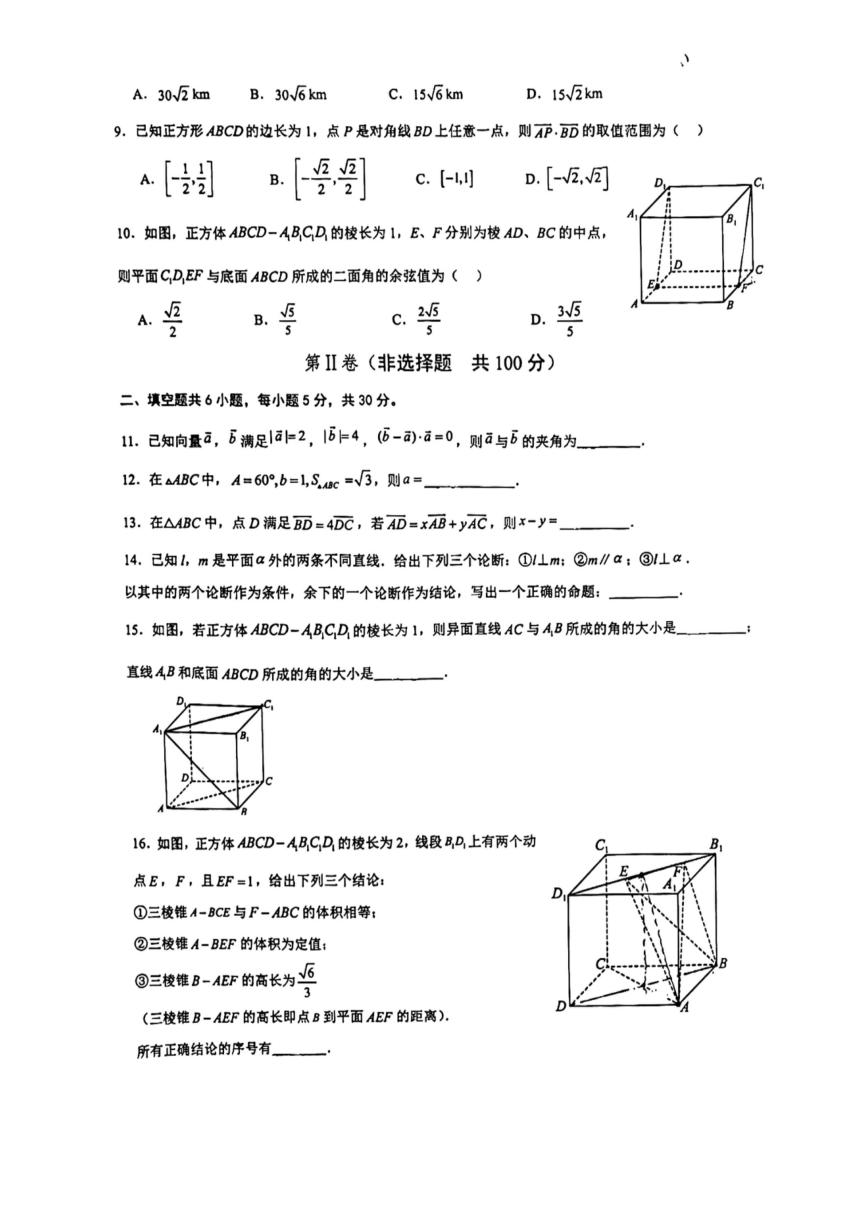
10.如图,正方体ABCD-ABCD的棱长为1,E、F分别为棱AD、BC的中点,
则平面C,D,EF与底面ABCD所成的二面角的余弦值为()
B.5
C.
D.35
第Ⅱ卷(非选择题共100分)
二、填空题共6小题,每小题5分,共30分。
11.已知向量a,6满足a非2,1b=4,(6-a)a=0,则a与6的夹角为。
12.在△MBC中,A=60°,b=l,S.c=√3,则a=_
13.在△ABC中,点D满足BD=4DC,若AD=xAB+yAC,则x-y=」
14.已知l,m是平面a外的两条不同直线.给出下列三个论断:①1⊥m:②m∥a;③lLc,
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:
15.如图,若正方体ABCD-AB,CD的棱长为1,则异面直线AC与A,B所成的角的大小是
直线AB和底面ABCD所成的角的大小是」
16.如图,正方体ABCD-AB,CD的棱长为2,线段BD,上有两个动
C
E
F
点E,F,且EF=1,给出下列三个结论:
①三棱锥A-BCE与F-ABC的体积相等:
②三棱锥A-BEF的体积为定值:
@三棱锥B-AEF的高长为5
(三棱锥B-AEF的高长即点B到平面AEF的距离).
所有正确结论的序号有_
2024年5月8日
高一数学
(北京第二外国语学院附属中学)
:·本试卷共4页,150分。考试时长120分钟。
第I卷(选择题共50分)
.一、选择题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项。
.15已知向量ā=0,-2),6=(x,4),且aii.,则a-=()
A.55
B.2√2
C.25
D.3W5
2.i是虚数单位,若复数(1-2i)(a+i)是纯虚数,则实数a的值为(、
A.2
B.-2
c.
D月
3,己知一个圆锥和圆柱的底面半径和高分别相等,若圆锥的轴截面是等边三角形,则这个圆锥和圆柱的
侧面积之比为()
A:克
B.2
C.
3
D.万
4.已知向量à=(2,4),6=(3,-1),则“k=√5"是“(a+k)1(a-k的()
A.充分不必要条件
B,必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
5.在aABC中,角A,B,C的对边分别为a,b,c,若a=2 bcosC,则△ABC一定是()
A,正三角形
B.直角三角形
C.等腰或直角三角形D.等腰三角形
6.如图,在正方体ABCD-ABCD中,点P是线段AC上的动点,下列与BP始终异面的是()
0
A.DD,
B.AC
C.AD
D.BC
7.已知两条直线m,n和平面a,那么下列命题中的真命题是()
A.若m⊥n,nca,则m⊥a
B.若m⊥n,n⊥a,则m/1a
C.若m⊥a,nca,则m⊥n
D.若m/la,n/1a,则m∥n
8.一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶4h后,船到达C处,
看到这个灯塔在北偏东15°,这时船与灯塔的距离为()
第1页共4页
A.30v2 km
B.306 km
C.156km
D.15√5km
9,已知正方形ABCD的边长为1,点P是对角线BD上任意一点,则P.BD的取值范围为()
a【
B
22
c.【l,
D.[-2
9
10.如图,正方体ABCD-ABCD的棱长为1,E、F分别为棱AD、BC的中点,
则平面C,D,EF与底面ABCD所成的二面角的余弦值为()
B.5
C.
D.35
第Ⅱ卷(非选择题共100分)
二、填空题共6小题,每小题5分,共30分。
11.已知向量a,6满足a非2,1b=4,(6-a)a=0,则a与6的夹角为。
12.在△MBC中,A=60°,b=l,S.c=√3,则a=_
13.在△ABC中,点D满足BD=4DC,若AD=xAB+yAC,则x-y=」
14.已知l,m是平面a外的两条不同直线.给出下列三个论断:①1⊥m:②m∥a;③lLc,
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:
15.如图,若正方体ABCD-AB,CD的棱长为1,则异面直线AC与A,B所成的角的大小是
直线AB和底面ABCD所成的角的大小是」
16.如图,正方体ABCD-AB,CD的棱长为2,线段BD,上有两个动
C
E
F
点E,F,且EF=1,给出下列三个结论:
①三棱锥A-BCE与F-ABC的体积相等:
②三棱锥A-BEF的体积为定值:
@三棱锥B-AEF的高长为5
(三棱锥B-AEF的高长即点B到平面AEF的距离).
所有正确结论的序号有_
同课章节目录
