数学:3.3.3《指数函数》课件(北师大版必修1)
文档属性
| 名称 | 数学:3.3.3《指数函数》课件(北师大版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 295.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 05:38:00 | ||
图片预览


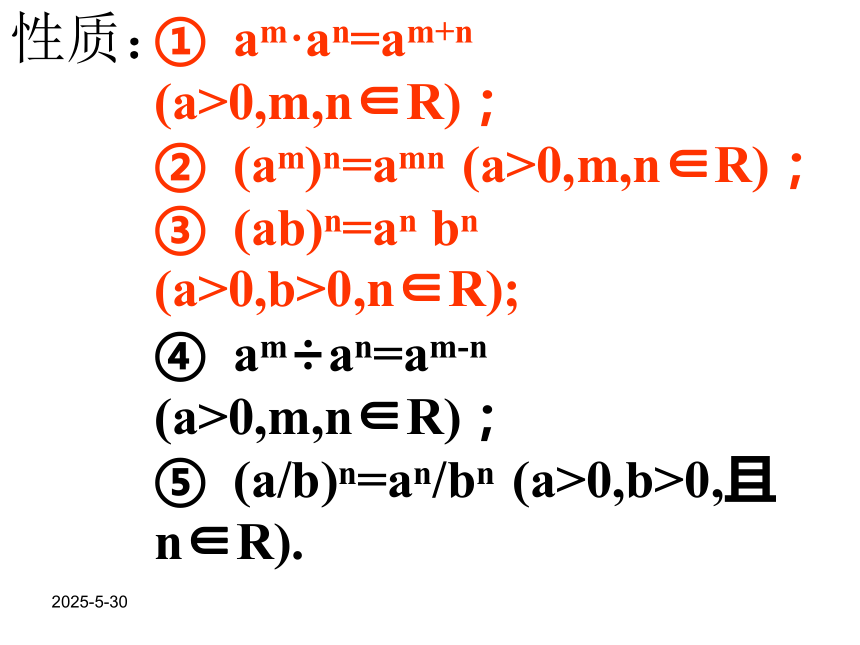


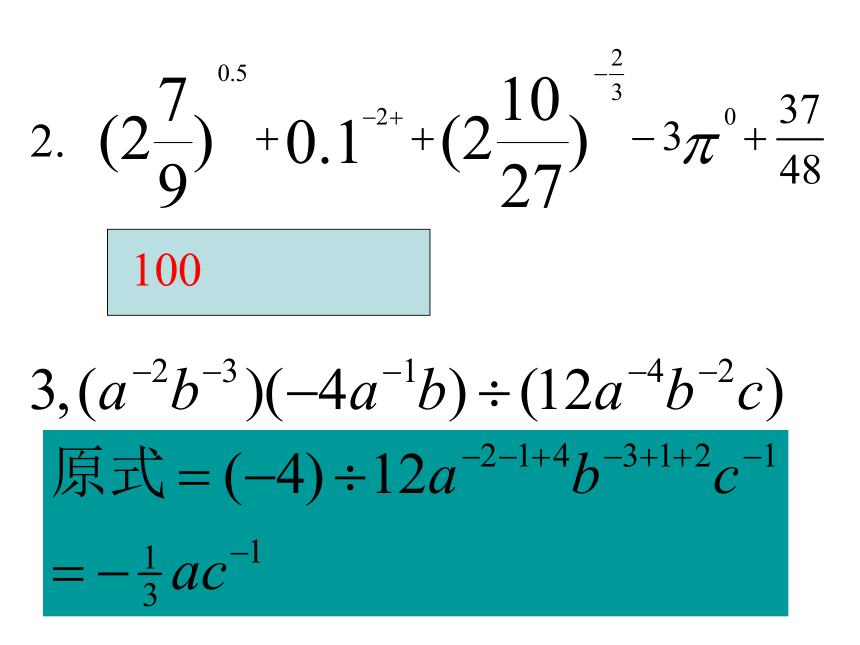


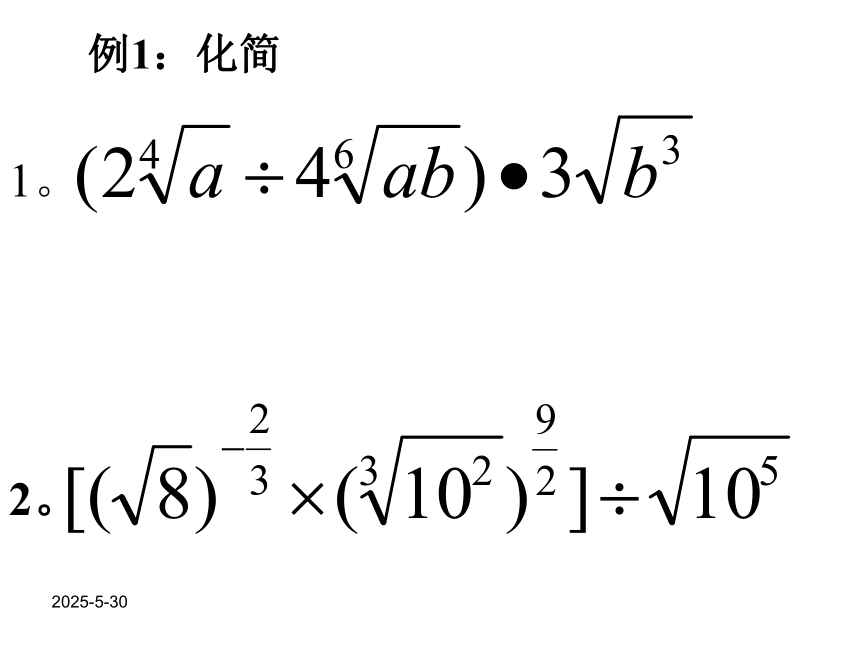
文档简介
课件27张PPT。§3.3.2指数函数2019-3-13规定正数的正分数指数幂的意义:规定正数的负分数指数幂的意义:0的正数次幂等于0,
0的负数次幂无意义,0的0次幂无意义。2019-3-13① am·an=am+n (a>0,m,n∈R);
② (am)n=amn (a>0,m,n∈R);
③ (ab)n=an bn (a>0,b>0,n∈R);
④ am÷an=am-n (a>0,m,n∈R);
⑤ (a/b)n=an/bn (a>0,b>0,且n∈R).
性质:2019-3-13题型一将根式转化分数指数幂的形式。(a>0,b>0)1,当有多重根式是,要由里向外层层转化。
2、对于有分母的,可以先把分母写成负指数幂。
3、要熟悉运算性质。题型二分数指数幂 求值, 关键先求a的n次方根2019-3-13题型三分数指数幂的运算1、系数先放在起运算。2、同底数幂
进行运算,乘的指数相加,除的指数相减。2019-3-132.1002019-3-13例4 计算例5 计算2019-3-13题型四根式运算,先把每个根式用分数指数幂表示;题目便转化为
分数指数幂的运算。
注意:结果可以用根式表示,也可以用分数指数幂表示。
但同一结果中不能既有根式又有分数指数幂,并且分
母中不能含有负分数指数幂。2019-3-13例1:化简2。1。2019-3-13例2:化简1。2。2019-3-13计算1。2。2019-3-13题型五利用代数公式进行化简:2019-3-13例1:化简2019-3-13例2:2019-3-13232019-3-137182019-3-13解:原式 =2019-3-134、已知 x -3 + 1 = a ,求 a 2 -2ax -3 + x -6 的值。解法一:a 2 -2ax -3 + x -6 = ( x -3 + 1 ) 2 -2( x -3 + 1 )x -3 + x -6= x -6 + 2x -3 + 1 -2 x -6 -2x -3 + x -6= 1解法二:由 x -3 + 1 = a 得x -3 = a -1x -6 = ( x -3 ) 2 = ( a -1 ) 2故 原式 = 1由题 a -x -3 = 1原式 = ( a -x -3 ) 2解法3:= 1= a 2 -2a 2 + 2a + a 2 -2a + 1 = a 2 -2a( a -1 ) + ( a -1 ) 2 a 2 -2ax -3 + x -6 2019-3-13题型六分数指数幂或根式中x的定义域问题。例:求下列各式中x的范围2019-3-13测试题2019-3-13 1. 已知 那么x等于
(A)8 (B) (C) (D)2.对任意实数a,下列等式正确的是
(A) (B)
(C) (D) 3.2019-3-136.已知 ,其中a>0, , 将下列各式分别用u表示出来:
(1) (2)
5.4.2019-3-139. 设 求 的值
10. 已知 且 a>0,
求 的值.
?
7.8.2019-3-1311.12.2019-3-13
0的负数次幂无意义,0的0次幂无意义。2019-3-13① am·an=am+n (a>0,m,n∈R);
② (am)n=amn (a>0,m,n∈R);
③ (ab)n=an bn (a>0,b>0,n∈R);
④ am÷an=am-n (a>0,m,n∈R);
⑤ (a/b)n=an/bn (a>0,b>0,且n∈R).
性质:2019-3-13题型一将根式转化分数指数幂的形式。(a>0,b>0)1,当有多重根式是,要由里向外层层转化。
2、对于有分母的,可以先把分母写成负指数幂。
3、要熟悉运算性质。题型二分数指数幂 求值, 关键先求a的n次方根2019-3-13题型三分数指数幂的运算1、系数先放在起运算。2、同底数幂
进行运算,乘的指数相加,除的指数相减。2019-3-132.1002019-3-13例4 计算例5 计算2019-3-13题型四根式运算,先把每个根式用分数指数幂表示;题目便转化为
分数指数幂的运算。
注意:结果可以用根式表示,也可以用分数指数幂表示。
但同一结果中不能既有根式又有分数指数幂,并且分
母中不能含有负分数指数幂。2019-3-13例1:化简2。1。2019-3-13例2:化简1。2。2019-3-13计算1。2。2019-3-13题型五利用代数公式进行化简:2019-3-13例1:化简2019-3-13例2:2019-3-13232019-3-137182019-3-13解:原式 =2019-3-134、已知 x -3 + 1 = a ,求 a 2 -2ax -3 + x -6 的值。解法一:a 2 -2ax -3 + x -6 = ( x -3 + 1 ) 2 -2( x -3 + 1 )x -3 + x -6= x -6 + 2x -3 + 1 -2 x -6 -2x -3 + x -6= 1解法二:由 x -3 + 1 = a 得x -3 = a -1x -6 = ( x -3 ) 2 = ( a -1 ) 2故 原式 = 1由题 a -x -3 = 1原式 = ( a -x -3 ) 2解法3:= 1= a 2 -2a 2 + 2a + a 2 -2a + 1 = a 2 -2a( a -1 ) + ( a -1 ) 2 a 2 -2ax -3 + x -6 2019-3-13题型六分数指数幂或根式中x的定义域问题。例:求下列各式中x的范围2019-3-13测试题2019-3-13 1. 已知 那么x等于
(A)8 (B) (C) (D)2.对任意实数a,下列等式正确的是
(A) (B)
(C) (D) 3.2019-3-136.已知 ,其中a>0, , 将下列各式分别用u表示出来:
(1) (2)
5.4.2019-3-139. 设 求 的值
10. 已知 且 a>0,
求 的值.
?
7.8.2019-3-1311.12.2019-3-13
