数学:3.4.3《对数》课件(北师大版必修1)
文档属性
| 名称 | 数学:3.4.3《对数》课件(北师大版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 146.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 00:00:00 | ||
图片预览








文档简介
课件24张PPT。2019/3/13对数2019/3/13学习目标什么是对数?
学会指数和对数互化.
对数的公式有那些?
利用对数的公式计算2019/3/13 引例:假设1995年我国的国民生产总值为 1亿元,
如每年平均增长8%,那么经过多少年国民
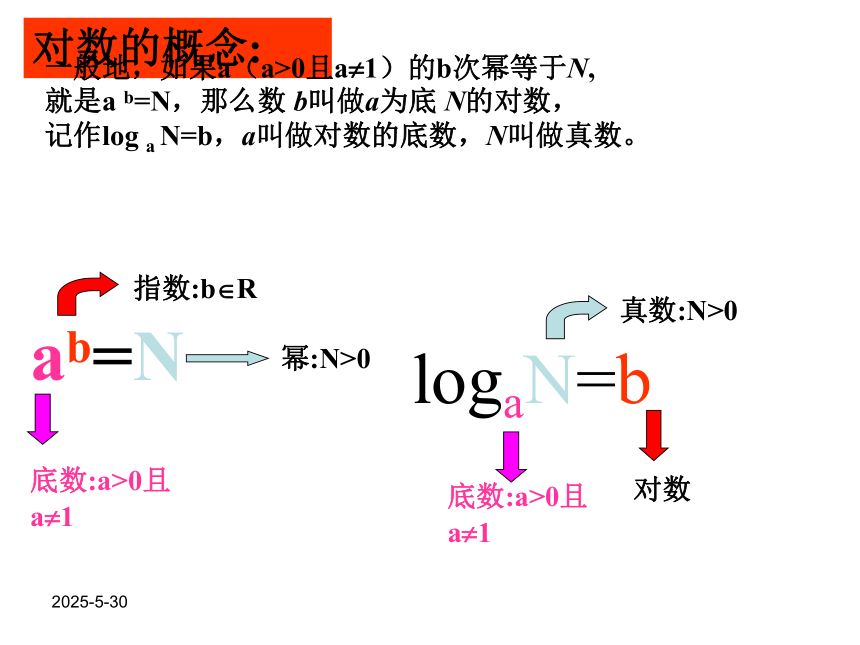
生产总值是1995年的2倍? 2019/3/13对数的概念: 一般地,如果a(a>0且a?1)的b次幂等于N,
就是a b=N,那么数 b叫做a为底 N的对数,
记作log a N=b,a叫做对数的底数,N叫做真数。2019/3/13性质:(1)负数与零没有对数;(2)1的对数是0;即loga1=0(3)底数的对数是1,即log a a=1(4)2019/3/13两个特殊对数:
以无理数e(e=2.71828‥‥‥ )为底的对数叫做自然对数,N的自然对数记作lnN. 以10为底的对数叫做常用对数,即N的常用对数记作lgN;
2019/3/13指数式与对数式的互化:例1:将下列指数式写成对数式: (1) 54=625 (2) ;
(3)3 a =27 ; (4) .例2.将下列对数式写成指数式:
(1) ; (2) ;
(3) ;(4) 2019/3/13例3:求下列各式的值:(1)log749=____ (2)lg100=________ (3)log0.351=____
(4) (5)log??=________ (6)lne=_______
(8)
(9)log2(sin300)=_______
2019/3/13积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:2019/3/13证明:①设 由对数的定义可以得: ∴MN= 即证得 2019/3/13上述证明是运用转化的思想,先通过假设,将对数
式化成指数式,并利用幂的运算性质进行恒等变形;
然后再根据对数定义将指数式化成对数式。①简易语言表达:“积的对数 = 对数的和”……②有时逆向运用公式 ③真数的取值范围必须是 ④对公式容易错误记忆,要特别注意:2019/3/13其他重要公式1:证明:设 由对数的定义可以得: ∴即证得 2019/3/13其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式2019/3/13其他重要公式3:证明:由换底公式 取以b为底的对数得: 还可以变形,得 2019/3/13例4 计算(1) (2) 讲解范例 解 :=5+14=19解 :2019/3/13讲解范例 (3) 解 :=32019/3/13例5 讲解范例 解(1) 解(2) 用 表示下列各式: 2019/3/13(1) 例6计算: 讲解范例 解法一: 解法二: 2019/3/13(2) 例3计算: 讲解范例 解: 2019/3/132019/3/13练习 (1) (4) (3) (2) 求下列各式的值:2019/3/13对数定义:一般地,如果a(a>0且a?1)的b次幂等于N,
就是a b=N,那么数 b叫做a为底 N的对数,
记作log a N=b,a叫做对数的底数,N叫做真数。性质:小结:2019/3/13积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:其他重要公式:2019/3/13预习提纲对数函数?
对数函数的图象?
对数函数的性质?
学会指数和对数互化.
对数的公式有那些?
利用对数的公式计算2019/3/13 引例:假设1995年我国的国民生产总值为 1亿元,
如每年平均增长8%,那么经过多少年国民
生产总值是1995年的2倍? 2019/3/13对数的概念: 一般地,如果a(a>0且a?1)的b次幂等于N,
就是a b=N,那么数 b叫做a为底 N的对数,
记作log a N=b,a叫做对数的底数,N叫做真数。2019/3/13性质:(1)负数与零没有对数;(2)1的对数是0;即loga1=0(3)底数的对数是1,即log a a=1(4)2019/3/13两个特殊对数:
以无理数e(e=2.71828‥‥‥ )为底的对数叫做自然对数,N的自然对数记作lnN. 以10为底的对数叫做常用对数,即N的常用对数记作lgN;
2019/3/13指数式与对数式的互化:例1:将下列指数式写成对数式: (1) 54=625 (2) ;
(3)3 a =27 ; (4) .例2.将下列对数式写成指数式:
(1) ; (2) ;
(3) ;(4) 2019/3/13例3:求下列各式的值:(1)log749=____ (2)lg100=________ (3)log0.351=____
(4) (5)log??=________ (6)lne=_______
(8)
(9)log2(sin300)=_______
2019/3/13积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:2019/3/13证明:①设 由对数的定义可以得: ∴MN= 即证得 2019/3/13上述证明是运用转化的思想,先通过假设,将对数
式化成指数式,并利用幂的运算性质进行恒等变形;
然后再根据对数定义将指数式化成对数式。①简易语言表达:“积的对数 = 对数的和”……②有时逆向运用公式 ③真数的取值范围必须是 ④对公式容易错误记忆,要特别注意:2019/3/13其他重要公式1:证明:设 由对数的定义可以得: ∴即证得 2019/3/13其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式2019/3/13其他重要公式3:证明:由换底公式 取以b为底的对数得: 还可以变形,得 2019/3/13例4 计算(1) (2) 讲解范例 解 :=5+14=19解 :2019/3/13讲解范例 (3) 解 :=32019/3/13例5 讲解范例 解(1) 解(2) 用 表示下列各式: 2019/3/13(1) 例6计算: 讲解范例 解法一: 解法二: 2019/3/13(2) 例3计算: 讲解范例 解: 2019/3/132019/3/13练习 (1) (4) (3) (2) 求下列各式的值:2019/3/13对数定义:一般地,如果a(a>0且a?1)的b次幂等于N,
就是a b=N,那么数 b叫做a为底 N的对数,
记作log a N=b,a叫做对数的底数,N叫做真数。性质:小结:2019/3/13积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:其他重要公式:2019/3/13预习提纲对数函数?
对数函数的图象?
对数函数的性质?
