数学:3.4.4《对数》课件(北师大版必修1)
文档属性
| 名称 | 数学:3.4.4《对数》课件(北师大版必修1) |
|
|
| 格式 | rar | ||
| 文件大小 | 131.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 00:00:00 | ||
图片预览




文档简介
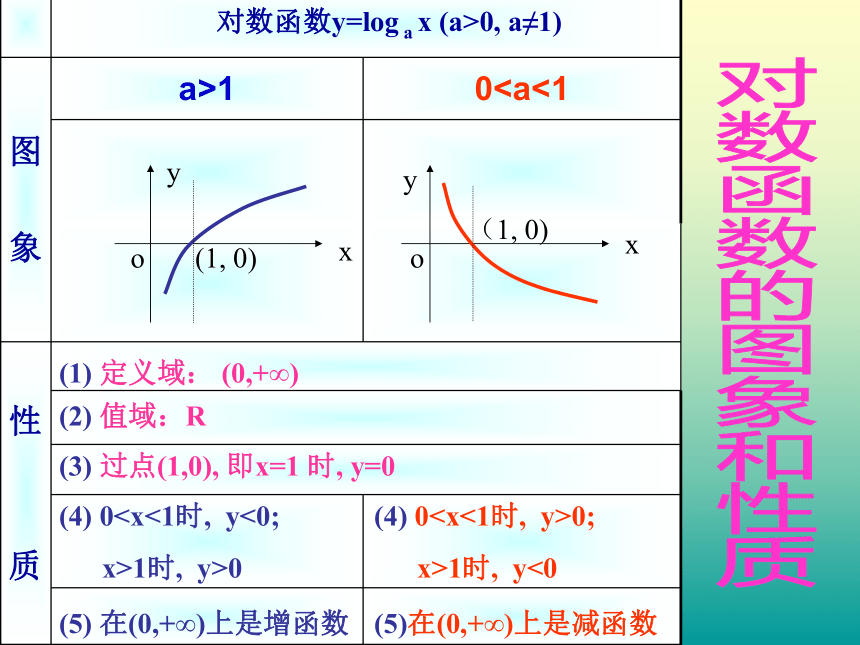
课件11张PPT。对数函数的性质应用对数函数y=log a x (a>0, a≠1)(4) 0 x>1时, y>0(4) 00;
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质例1 比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )解 ⑴考察对数函数 y = log 2x,因为它的底数2>1,
所以它在(0,+∞)上是增函数,于是
log 23.4<log 28.5 ⑵考察对数函数 y = log 0.3 x,因为它的底数0.3,
即0<0.3<1,所以它在(0,+∞)上是减函数,于是
log 0.31.8>log 0.32.7探求之一:底数相同的两个对数比较解:当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
log a5.1<log a5.9
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
log a5.1>log a5.9⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )分析:对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
小结:怎样比较同底的两个对数的大小?(1)确定函数的底数是否大于1:(2)判断对数函数的增减;(3)确定两数的大小;练习1:
比较下列各题中两个值的大小:
⑴ log106 log108
⑵ log0.56 log0.54
⑶ log0.10.5 log0.10.6
⑷ log1.51.6 log1.51.4
<<>>例2 比较下列各组中两个值的大小:
(1) log 3π , log 2 0.8 .
(2)log 67 , log 7 6 ; 解:(1)∵ log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8分析:㏒3 π>1=㏒33
㏒3π>0㏒20.8<0探求之二:不同底的两个对数比较解:∵ log67>log66=1
log76<log77=1
∴ log67>log76(2)log 67 , log 7 6 ; 分析: log 67>1 log 7 6 <1小结:若底数不同,真数也不同的两个对数比较大小时,先作相对应的函数图进行估值,再采用插入中间变量“0”或“1”来确定两对数值得大小。 练习2:
(1)㏒0.30.7 , ㏒2.12.9解:㏒0.30.7<㏒0.30.3=1
㏒2.12.9>㏒2.12.1=1
㏒0.30.7 < ㏒2.12.9探求之三:底数不同但真数相同例3 ㏒1.10.7 , ㏒1.20.7
解:由图可知: ㏒1.10.7 < ㏒1.20.7小结:底数不同但真数相同的题目中,一般
采用作图法。练习3:
(1)㏒1.1 2.3 ,㏒1.2 2.2解:㏒1.1 2.3>㏒1.1 2.2㏒1.12.2> ㏒1.2 2.2
㏒1.1 2.3> ㏒1.2 2.2小 结比较两个对数值的大小1、若底数为同一常数,则可由对数函数的单调性直接进行判断2、若底数为同一字母,则按对数函数的单调性对底数进行分类讨论3、若底数、真数都不相同,则常借助1、0、-1等中间量进行比较. 4、若底数不同真数相同,则常借助对数函数图象进行比较
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质例1 比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )解 ⑴考察对数函数 y = log 2x,因为它的底数2>1,
所以它在(0,+∞)上是增函数,于是
log 23.4<log 28.5 ⑵考察对数函数 y = log 0.3 x,因为它的底数0.3,
即0<0.3<1,所以它在(0,+∞)上是减函数,于是
log 0.31.8>log 0.32.7探求之一:底数相同的两个对数比较解:当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
log a5.1<log a5.9
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
log a5.1>log a5.9⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )分析:对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
小结:怎样比较同底的两个对数的大小?(1)确定函数的底数是否大于1:(2)判断对数函数的增减;(3)确定两数的大小;练习1:
比较下列各题中两个值的大小:
⑴ log106 log108
⑵ log0.56 log0.54
⑶ log0.10.5 log0.10.6
⑷ log1.51.6 log1.51.4
<<>>例2 比较下列各组中两个值的大小:
(1) log 3π , log 2 0.8 .
(2)log 67 , log 7 6 ; 解:(1)∵ log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8分析:㏒3 π>1=㏒33
㏒3π>0㏒20.8<0探求之二:不同底的两个对数比较解:∵ log67>log66=1
log76<log77=1
∴ log67>log76(2)log 67 , log 7 6 ; 分析: log 67>1 log 7 6 <1小结:若底数不同,真数也不同的两个对数比较大小时,先作相对应的函数图进行估值,再采用插入中间变量“0”或“1”来确定两对数值得大小。 练习2:
(1)㏒0.30.7 , ㏒2.12.9解:㏒0.30.7<㏒0.30.3=1
㏒2.12.9>㏒2.12.1=1
㏒0.30.7 < ㏒2.12.9探求之三:底数不同但真数相同例3 ㏒1.10.7 , ㏒1.20.7
解:由图可知: ㏒1.10.7 < ㏒1.20.7小结:底数不同但真数相同的题目中,一般
采用作图法。练习3:
(1)㏒1.1 2.3 ,㏒1.2 2.2解:㏒1.1 2.3>㏒1.1 2.2㏒1.12.2> ㏒1.2 2.2
㏒1.1 2.3> ㏒1.2 2.2小 结比较两个对数值的大小1、若底数为同一常数,则可由对数函数的单调性直接进行判断2、若底数为同一字母,则按对数函数的单调性对底数进行分类讨论3、若底数、真数都不相同,则常借助1、0、-1等中间量进行比较. 4、若底数不同真数相同,则常借助对数函数图象进行比较
