数学:3.5.1《对数函数》课件(北师大版必修1)
文档属性
| 名称 | 数学:3.5.1《对数函数》课件(北师大版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 139.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 00:00:00 | ||
图片预览





文档简介
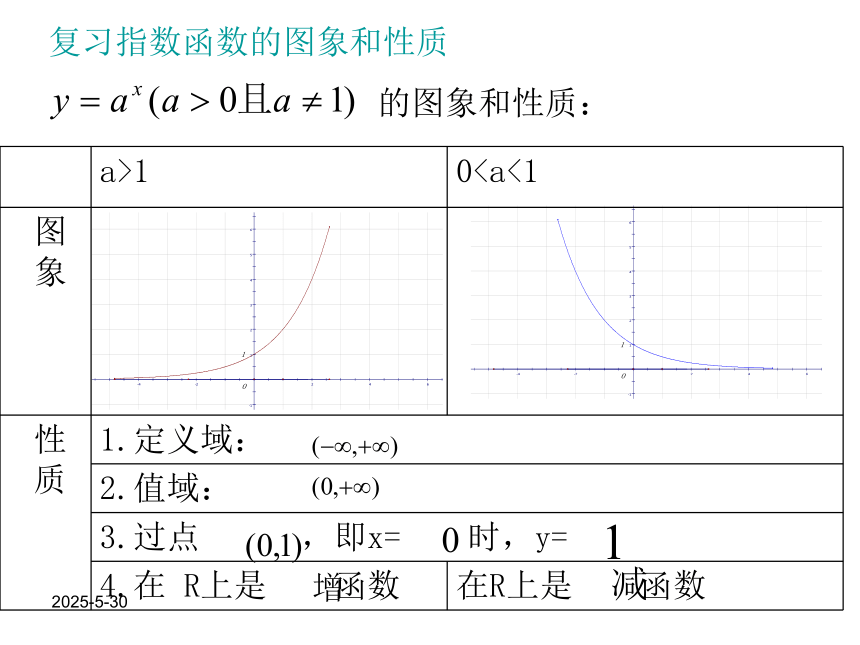
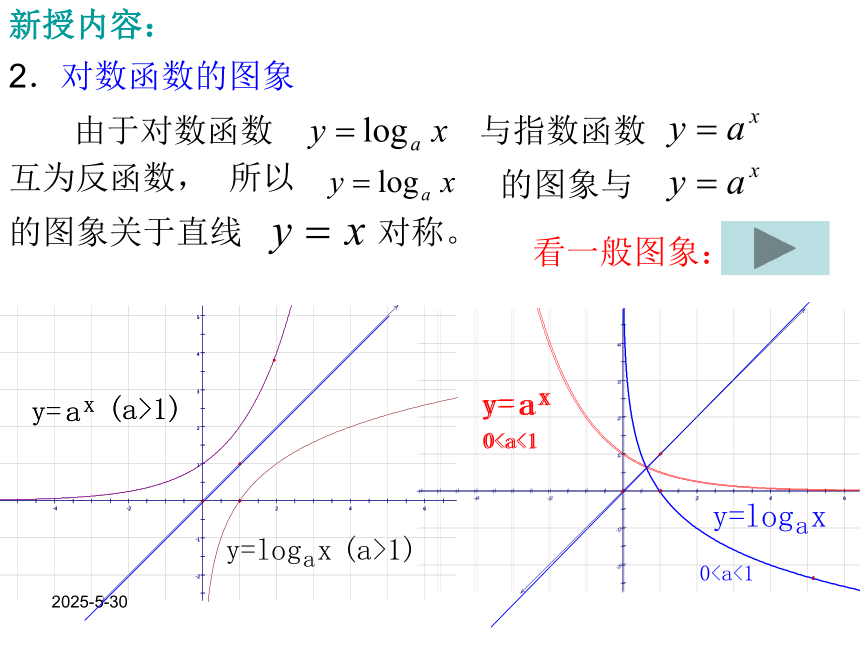
课件15张PPT。2019/3/13对数函数 2019/3/13一般地,如果 的b次幂等于N, 就是 ,那么数 b叫做以a为底 N的对数,记作 a叫做对数的底数,N叫做真数。定义:复习对数的概念2019/3/13⑴负数与零没有对数⑵ ⑶对数恒等式复习对数的性质⑷常用对数: =lgN⑸自然对数: =lnN(6)底数a的取值范围: 真数N的取值范围 :2019/3/13复习对数运算法则2019/3/13的图象和性质: 复习指数函数的图象和性质2019/3/13新授内容: 1.对数函数的定义:函数 叫做对数函数; 它是指数函数 的反函数。的定义域为 值域为 2019/3/13新授内容: 2.对数函数的图象由于对数函数 与指数函数 互为反函数, 所以 的图象与 的图象关于直线 对称。 看一般图象:2019/3/13新授内容: 3.对数函数的性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减2019/3/13例1求下列函数的定义域:(1) (2) 讲解范例 解 :解 :由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是(3) 解 :由 得 ∴函数 的定义域是2019/3/13讲解范例 (1) 解 :例2求下列函数的反函数(1) (2) (2) 2019/3/13例3 讲解范例 解(1) 解(2) 比较下列各组数中两个值的大小: (1) (2)考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是 2019/3/13练习 1.画出函数 的图象,并且说明这两个函数的相同性质和不同性质.解:相同性质: y轴右方,都经过点(1,0),
这说明两函数的定义域
都是(0,+∞),且当
x=1,y=0.不同性质: 两图象都位于的图象是上升的曲线, 在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞)上是减函数.2019/3/13练习 2.求下列函数的定义域:(1)(2)(3)(4)2019/3/13小结 :1.对数函数的定义:函数 叫做对数函数; 它是指数函数 的反函数。的定义域为 值域为 2019/3/13小结 :2.对数函数的图象和性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减
(0,+∞)过点(1,0),即当x=1时,y=0 增减2019/3/13例1求下列函数的定义域:(1) (2) 讲解范例 解 :解 :由 得 ∴函数 的定义域是由 得 ∴函数 的定义域是(3) 解 :由 得 ∴函数 的定义域是2019/3/13讲解范例 (1) 解 :例2求下列函数的反函数(1) (2) (2) 2019/3/13例3 讲解范例 解(1) 解(2) 比较下列各组数中两个值的大小: (1) (2)考查对数函数 因为它的底数2>1,所以它在(0,+∞)上是增函数,于是 考查对数函数 因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是 2019/3/13练习 1.画出函数 的图象,并且说明这两个函数的相同性质和不同性质.解:相同性质: y轴右方,都经过点(1,0),
这说明两函数的定义域
都是(0,+∞),且当
x=1,y=0.不同性质: 两图象都位于的图象是上升的曲线, 在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞)上是减函数.2019/3/13练习 2.求下列函数的定义域:(1)(2)(3)(4)2019/3/13小结 :1.对数函数的定义:函数 叫做对数函数; 它是指数函数 的反函数。的定义域为 值域为 2019/3/13小结 :2.对数函数的图象和性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减
