数学:3.5.2《对数函数》课件(北师大版必修1)
文档属性
| 名称 | 数学:3.5.2《对数函数》课件(北师大版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 383.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-23 05:39:00 | ||
图片预览




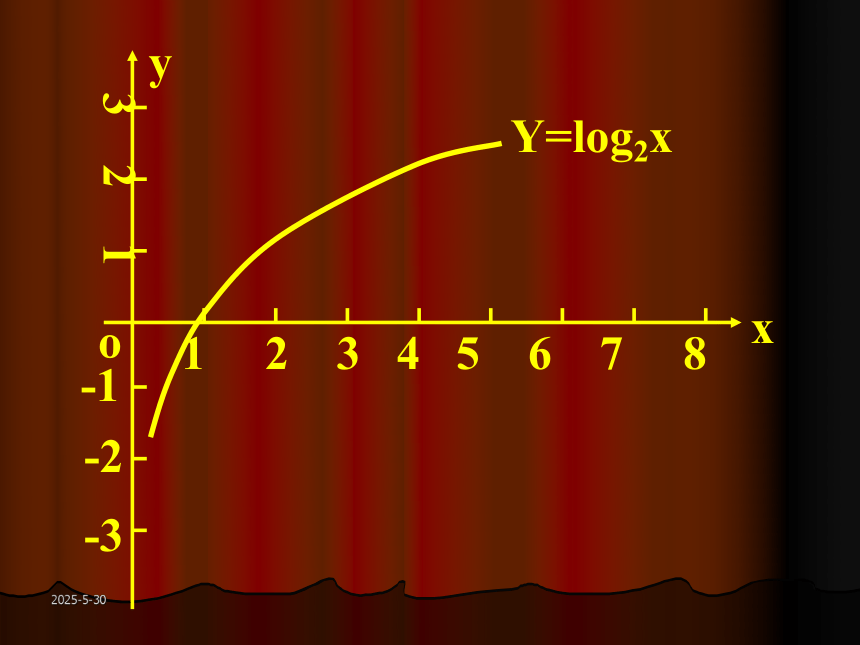

文档简介
课件21张PPT。 对数函数2019-3-13一?定义:函数 y= logax(a>0,a≠??,定义域是(0,+??,叫对数函数。2019-3-13判断:以下函数是对数函数的是 ( )
A y=log2(3x-2) B y=log(x-1)x
C y=log1/3x2 D y=lnx2019-3-132019-3-132019-3-132019-3-132019-3-132019-3-13因为指数函数y=ax (0●
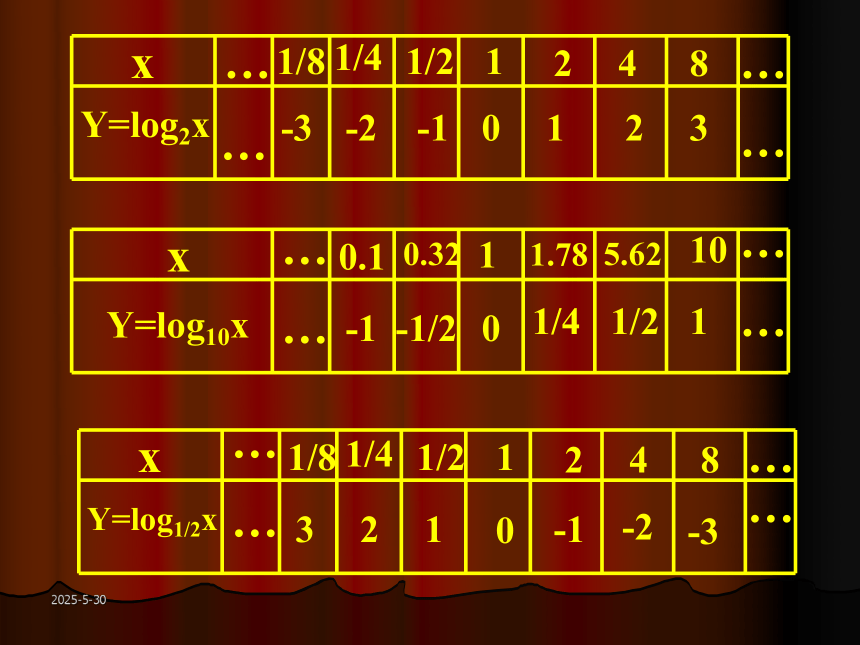
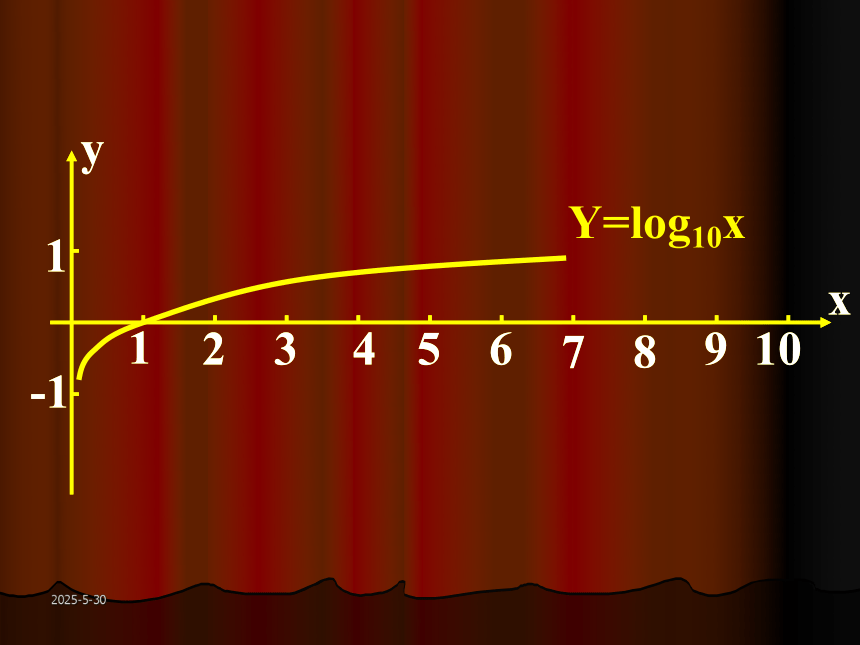
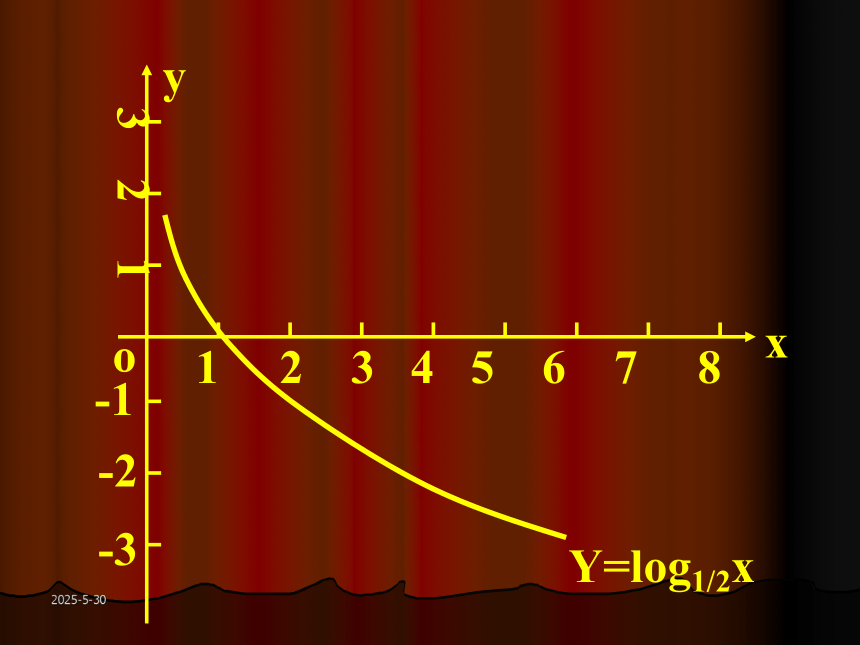
2019-3-13OXY123456789123-1-2-3Y=log2xY=lgxY=log1/2x2019-3-13三.对数函数的性质:观察图象,总结性质.2019-3-13a>100x=1时,y=0x>1时,y>0
00
x>1时,y<0在(0,+??上是增函数在(0,+??上是减函数2019-3-13其它性质:(1)随着底数a的增大,图象在同一象限内的位置按顺时针转。(2)y=logax与y=log1/ax的图象关于x轴对称。(3)对数函数是非奇非偶函数。2019-3-13 例一:求下列函数的定义域:(1) y=logax2 (2) y=loga(4-x)解:(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为 ?-???? ? (0,+?? (2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为(-??4) (3) y=log(x-1)(3-x) (4) y=?log0.5(4x-3)2019-3-13(3) 因为 3-x>0
x-1>0
x-1≠?所以 10
log0.5(4x-3)?0x>3/4
4x-3≤?定义域为(3/4,1]2019-3-13例2:比较下列各组中两个值的大小: (1) log23 , log23.5 (2) log0.71.6 , logo.71.8 解:(1)考察对数函数y=log2x,因为 2>1, 3<3.5所以log23log0.71.82019-3-13思考题2019-3-13小结
(2)对数函数的图象和性质.(3)性质的应用.(1)对数函数的定义.2019-3-13注意(2)看见函数式想图象,结合图象记性质。(1) 类比记忆指数函数和对数函数。2019-3-13作业P97 1 , 22019-3-13
A y=log2(3x-2) B y=log(x-1)x
C y=log1/3x2 D y=lnx2019-3-132019-3-132019-3-132019-3-132019-3-132019-3-13因为指数函数y=ax (0
2019-3-13OXY123456789123-1-2-3Y=log2xY=lgxY=log1/2x2019-3-13三.对数函数的性质:观察图象,总结性质.2019-3-13a>10
0
x>1时,y<0在(0,+??上是增函数在(0,+??上是减函数2019-3-13其它性质:(1)随着底数a的增大,图象在同一象限内的位置按顺时针转。(2)y=logax与y=log1/ax的图象关于x轴对称。(3)对数函数是非奇非偶函数。2019-3-13 例一:求下列函数的定义域:(1) y=logax2 (2) y=loga(4-x)解:(1)因为x2>0,所以x≠?,即函数y=logax2的定义域为 ?-???? ? (0,+?? (2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为(-??4) (3) y=log(x-1)(3-x) (4) y=?log0.5(4x-3)2019-3-13(3) 因为 3-x>0
x-1>0
x-1≠?所以 1
log0.5(4x-3)?0x>3/4
4x-3≤?定义域为(3/4,1]2019-3-13例2:比较下列各组中两个值的大小: (1) log23 , log23.5 (2) log0.71.6 , logo.71.8 解:(1)考察对数函数y=log2x,因为 2>1, 3<3.5所以log23
(2)对数函数的图象和性质.(3)性质的应用.(1)对数函数的定义.2019-3-13注意(2)看见函数式想图象,结合图象记性质。(1) 类比记忆指数函数和对数函数。2019-3-13作业P97 1 , 22019-3-13
