2023-2024学年苏教版小学数学五年级下册第七单元《解决问题的策略》检测卷(含答案解析)
文档属性
| 名称 | 2023-2024学年苏教版小学数学五年级下册第七单元《解决问题的策略》检测卷(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 817.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 12:51:27 | ||
图片预览




文档简介
2023-2024学年五年级下册数学单元检测卷
第七单元《解决问题的策略》
姓名:_________ 班级:_________ 学号:_________
一、填空题(满分20分)
1.(2分)观察下面的算式:
5×9=45
55×99=5445
555×999=554445
5555×9999=55544445
……
则555555×999999=_________.
2.(2分)小亮用计算器算出了四个算式的结果:7×202=1414,12×202=2424,23×202=4646,36×202=7272。根据这些算式的规律可知45×202=_________。
3.(2分)根据算式的规律填空。
,,, 。
4.(2分),按照这样的规律, 。
5.(2分)5个同样的小长方形拼成一个面积为的大长方形(如图),阴影部分的面积是 。
6.(2分)街心公园里有一种“围树座椅”,形状如图。这种“围树座椅”椅面的面积是 。
7.(2分)非遗文化之手工剪纸。盈盈用一张直径是的圆形纸片剪出如图所示的“风车”图案(空白部分),则被剪掉的纸片(阴影部分)的面积是 。
8.(2分)一种可以折叠的圆形餐桌,桌面直径2米,把四周折叠后就是一个正方形餐桌(如图)。这个餐桌的折叠部分(阴影部分)的面积是 平方米。
9.(2分)已知,,,那么 , 。
10.(2分)根据算式的规律填空:,,在计算中,写出〇、□表示的整数:〇 ,□ 。
二、判断题(满分10分)
11.(2分)如图是由7个同样的正方形拼成的,涂色部分甲与涂色部分乙的面积相等。
12.(2分)如图是三个完全相同的长方形,它们阴影部分的面积相等. .
13.(2分)由,,能推出。
14.(2分)在中,从“1”到数“13”的和是49. .
15.(2分)求下面图形的周长和面积.(单位:厘米.2只求面积)
三、选择题(满分10分)
16.(2分)不计算,用发现的规律得到最后一道题的商是()
?
A.0.2020 B. C. D.
17.(2分)仔细观察下面这组算式:
根据规律接着往下写,第4个算式是()
A. B.
C. D.
18.(2分)根据,那么
A. B. C.
19.(2分)下列各图中的正方形面积相等,图()的阴影面积与另外三图不同.
A. B. C. D.
20.(2分)如图,圆的直径是7厘米,正方形的面积是()平方厘米。
A.21.98 B.10.99 C.49 D.24.5
四、计算题(满分24分)
21.(6分)求如图中阴影部分的面积(图中单位:。
22.(6分)找规律,写得数。
。
23.(6分)先计算,再思考后完成填空.
根据:,,
可以得出:
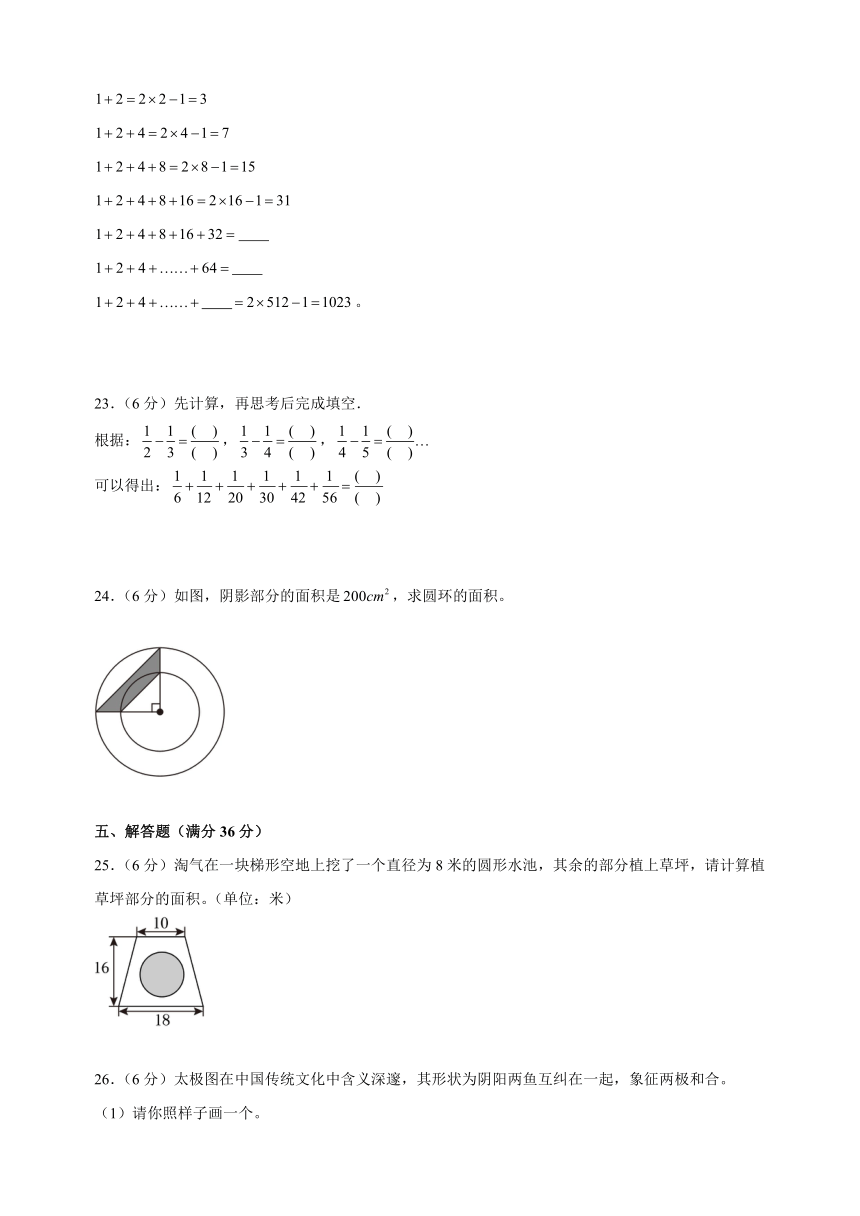
24.(6分)如图,阴影部分的面积是,求圆环的面积。
五、解答题(满分36分)
25.(6分)淘气在一块梯形空地上挖了一个直径为8米的圆形水池,其余的部分植上草坪,请计算植草坪部分的面积。(单位:米)
26.(6分)太极图在中国传统文化中含义深邃,其形状为阴阳两鱼互纠在一起,象征两极和合。
(1)请你照样子画一个。
(2)如果大圆半径是6厘米,请求出阴鱼(即阴影部分)的面积。
求面积的计算过程是:
27.(6分)如图,一张可折叠的圆桌折叠后成了正方形,如果正方形的边长是1.2米,那么圆桌原来的面积是多少平方米?(结果保留两位小数。
28.(6分)先计算—探究规律,然后运用规律—完成填空。
;
;
;
。
29.(6分)先阅读理解,再解决问题。
有这样的一组算式:
;
;
;
;
(1)我发现:像上面这种加法的和数,等于 乘 。
(2)根据规律直接写出下面几题的结果。
。
。
30.(6分)亲爱的同学们,在小学阶段我们认识了许多新的数,比如质数(素数)、合数、奇数、偶数等。下面的数你能找到其中的规律吗?写出你的猜想。
8=3+5;10=3+7;12=5+7;14=3+11;16=3+13=5+11;18=5+13=7+11
20=3+17=7+13;22=3+19=5+17;24=5+19=7+17=11+13;26=______+______=______+______……你的猜想是:任何一个大于6的偶数可以______。
我国数学家陈景润在这一方面做了深入的研究,这种探索和钻研精神非常值得我们同学们学习。1742年,德国数学家哥德巴赫发现了这个规律,这个设想被简称为“1+1”,也就是著名的“哥德巴赫猜想”。请你仿照例子填空:30=______+______,40=______+______。
参考答案
一、填空题(满分20分)
1.【分析】通过仔细观察,得出规律:n个5×n个9=(n-1)个5,n个4,最后是一个5.因此,当n=6时,据此规律,很快就可写出.
【解答】解:555555×999999=555554444445;
故答案为:555554444445.
【点评】此题属于找规律的题目,解答这类问题,应仔细观察给出的例子,找出规律,据规律解答.
2.【分析】观察四个算式可知,算式的第二个因数都是202,把第一因数乘2的积写2次,即为算式的积。
【解答】解:,所以。
故答案为:9090。
【点评】找出积与因数之间的关系,本题主要考查学生分析归纳能力。
3.【分析】根据,,可以发现的规律,据此解答即可。
【解答】解:,,,。
故答案为:;。
【点评】本题考查了算式的规律,结合题意分析解答即可。
4.【分析】根据,可知,从开始,依次加前面加数的,最后的结果等于1减去最后的分数,按照这样的规律,解答即可。
【解答】解:分析可知,。
故答案为:,。
【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题。
5.【分析】阴影部分的面积占4个长方形面积的一半,先求出1个小长方形的面积再乘4求出4个长方形的面积,最后再除以2即可。
【解答】解:
答:阴影部分的面积是。
故答案为:16。
【点评】本题考查的是组合图形的面积的应用。
6.【分析】根据圆环的面积公式即可解答。
【解答】解:大圆半径:(米
小圆半径:(米
圆环面积
(平方米)
答:这种“围树座椅”椅面的面积是。
故答案为:9.42。
【点评】本题主要考查圆环的面积公式。
7.【分析】根据图示,阴影部分的面积等于半径是(厘米)的圆的面积减去2个半径是(厘米)的圆的面积,据此解答即可。
【解答】解:大圆半径是:
(厘米)
小圆半径是:
(厘米)
(平方厘米)
答:被剪掉的纸片(阴影部分)的面积是157平方厘米。
故答案为:157。
【点评】本题考查了组合图形面积计算知识,结合圆的面积公式解答即可。
8.【分析】阴影部分的面积圆的面积正方形面积,把正方形分成两个完全一样的三角形,每个三角形的底等于圆的直径,每个三角形的高等于圆的半径,根据圆的面积公式:,三角形的面积公式:,把数据代入公式解答。
【解答】解:
(平方米)
答:这个餐桌的折叠部分(阴影部分)的面积是1.14平方米。
故答案为:1.14。
【点评】此题主要考查圆的面积公式、正方形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式。
9.【分析】根据题意,,,,由此发现规律:,据此解答即可。
【解答】解:已知,,,那么,。
故答案为:444444,。
【点评】根据所给的算式,发现规律是,然后利用规律解答即可。
10.【分析】根据题意,,,可以发现如下规律:,据此解答即可。
【解答】解:分析可以发现如下规律:,所以在计算中,写出〇、□表示的整数:〇,□。
故答案为:7;42。
【点评】本题考查了算式中的规律知识,结合题意分析解答即可。
二、判断题(满分10分)
11.【分析】等底等高的三角形面积相等。同样的正方形,则每个正方形的边长相等。甲三角形的底是2个正方形的边长,高是1个正方形的边长。乙三角形是底也是2个正方形的边长,高是1个正方形的边长。结合三角形的面积底高,解答即可。
【解答】解:设正方形的边长为1。
甲三角形的底是2个正方形的边长,高是1个正方形的边长。甲面积:
乙三角形是底也是2个正方形的边长,高是1个正方形的边长。乙面积:
答:涂色部分甲与涂色部分乙的面积相等。所以原题说法正确。
故答案为:。
【点评】本题考查了组合图形面积计算知识,结合三角形的面积公式解答即可。
12.【分析】图中的阴影部分均为三角形,根据三角形的面积公式可知三角形的面积是由三角形的底和高决定的,图中阴影部分的三角形的底相等,高相等,所以面积也相等.
【解答】解:三角形的面积底高,
图中阴影部分的三角形,底相等,高相等,
所以阴影部分的面积也相等.
故判:.
【点评】此题主要考查的是等底等高的三角形的面积也相等.
13.【分析】依据题意可知,利用除法的计算方法计算的商,由此解答本题。
【解答】解:
,本题说法错误。
故答案为:。
【点评】本题从题中算式可知,被除数是几,商的小数部分就是被除数的9倍。
14.【分析】在中首先求出“13”是第几项(由于项数比较少,可能用数的方法),由于相邻两数的差是1,所以项数等于(末项首项),据即可求13是第几项;前项和的计算公式是(末项首项),根据公式可求出前13项的和,根据计算结果进行判断.
【解答】解:在中,从“1”到数“13”的项数为:
前6项的和为:
因此,在中,从“1”到数“13”的和是49,原题的说法是正确的.
故答案为:.
【点评】此题项数较少,写出所有项,通过计算即可得到正确的结果.如果项数较多,只能先总结出求项数、前项和公式解答.
15.【分析】(1)这个图形的周长等于直径2厘米的半圆的弧长与两条2.5厘米和一条2厘米的线段的长度之和,面积等于这个半圆的面积与下面的长方形的面积之和,据此计算即可解答;
(2)阴影部分的面积等于直径10厘米的圆的面积与中间的正方形的面积之差,正方形的面积可以看做两个直角三角形的面积来计算,这两个三角形的底都是10厘米,高都是厘米,所以这个正方形的面积平方厘米,据此计算即可解答.
【解答】解:(1)阴影部分的周长是:
(厘米)
面积是:
(平方厘米)
(2)面积是:
(平方厘米)
【点评】此题主要考查图形的周长和面积,求阴影部分的周长时容易错,关键要理解周长的意义,即围成图形一周的长度.
三、选择题(满分10分)
16.【分析】观察题中算式可知,除数都是99,商是循环小数,循环节是被除数,由此解答本题。
【解答】解:由分析可知,
故选:。
【点评】解决本题的关键是找出题中的规律,利用规律去解答。
17.【分析】根据题目给出的算式发现,每个算式第二个数都是8,第一个数位数依次递增,可以推测第四个式子的第一个数是1234,第三个数依次递加1,可以推测第四个式子的第三个数是4,得数的位数也分别递增,而且第几个式子得数就是几位数,应为9876。
【解答】解:
根据分析,第4个算式是。
故选:。
【点评】此题考查式的规律,找出规律是解决此类题目的关键。
18.【分析】,即是正整数),由此求解。
【解答】解:根据,
那么。
故选:。
【点评】解决本题先从已知的算式中找出规律,再根据规律求解。
19.【分析】从图中可以看出阴影部分的面积正方形的面积圆的面积.观察图形可发现:四个正方形是全等的,面积是相等;、、三个图形中空白部分可以组成一个完整的圆,根据圆的面积相等可得这三个图形中阴影部分的面积相等,得出答案.
【解答】解:由图可知:从左到右、、的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,
根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等.
故选:.
【点评】此题考查了面积及等积变换,将阴影面积转化为易求的图形的面积的差或和是解题的常用方法.
20.【分析】由图可知,图中的大正方形是由4个底和高都等于圆半径的三角形组成,据此计算。
【解答】解:
(平方厘米)
答:正方形的面积是24.5平方厘米。
故选:。
【点评】解答本题的关键是分析出小正方形的底和高与圆的直径之间的关系。
四.计算题(满分24分)
21.【分析】根据图示,阴影部分的面积等于正方形的面积减去半径是(厘米)的圆的面积,根据正方形的面积公式:,圆的面积公式:,解答即可。
【解答】解:半径是:
(厘米)
阴影部分的面积:
(平方厘米)
答:阴影部分的面积是21.5平方厘米。
【点评】本题考查了正方形和圆的面积公式的灵活运用,结合题意分析解答即可。
22.【分析】连加算式的第一个加数都是1,后面的每一个加数都是前面一个加数的2倍,不难发现:这样的连加算式都可以用最后一个加数乘2减1来计算。
【解答】解:
故答案为:63;127;512。
【点评】解决本题的关键是根据数据之间的特征,推理出转化的规律。
23.【分析】各式都是两个分数相减,各分数的分子都是1,分母是从2开始的相邻两个自然数.通过计算可知,两个分数之差的分子是两分母之差,分母是两分母之积.根据这一规律,把中的看作、看作、看作然后即可计算等于几.
【解答】解:,,
.
故答案为:,,,.
【点评】解答此题的关键是根据前面的三个算式摸出此类分数相减的规律,然后再把下面一个算式的各分数分解成两个分数之差,然后即可进行计算.
24.【分析】根据阴影部分的面积为大三角形的面积减去小三角形的面积,大三角形的面积等于大圆半径的平方除以2,小三角形面积同理即可解答。
【解答】解:
(平方厘米)
圆环面积:(平方厘米)
答:圆环的面积是1256平方厘米。
【点评】本题主要考查阴影部分的面积为大三角形的面积减去小三角形的面积。
五.解答题(满分36分)
25.【分析】根据图示,草坪部分的面积等于梯形的面积减去直径为8米的圆形水池面积,据此解答即可。
【解答】解:
(平方米)
答:草坪部分的面积是173.76 平方米。
【点评】本题考查了组合图形面积计算知识,结合题意分析解答即可。
26.【分析】(1)画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
据此先画出一个大圆,在大圆中画出一条竖直的直径,分别以两条半径的中点为圆心,向右和向左画出两个半圆,再以两个半圆的圆心为圆心分别画出两个小圆即可,据此作图。
(2)根据图示,阴鱼的面积大圆面积的一半,根据圆的面积圆周率半径的平方,求出大圆面积,除以2即可。
【解答】解:(1)照样子画一个,如图:
(2)
(平方厘米)
答:如果大圆半径是6厘米,阴鱼的面积是56.52平方厘米。
【点评】此题主要考查了圆的画法以及圆的面积公式的灵活运用,关键是熟记公式。
27.【分析】设圆桌的半径是米,圆桌的直径等于正方形的对角线的长,根据“正方形的面积边长边长正方形对角线的长对角线长的一半”,据此求出半径的平方,再根据“圆的面积半径的平方”解答。
【解答】解:设圆桌的半径是米。
(平方米)
答:那么圆桌原来的面积大约是2.26平方米。
【点评】根据“正方形的面积边长边长正方形对角线的长对角线长的一半”求出圆桌的半径的平方是解题的关键。
28.【分析】根据异分母分数加法的计算方法,求出第一个算式的结果,发现结果的分母与最后一个加数的分母相同,分子比分母少1,后边都是这个规律;到最后一个算式,,加,结果就是1,据此分析解答即可。
【解答】解:
故答案为:;;;。
【点评】本题考查了算式的规律知识,结合题意找出规律,然后分析解答即可。
29.【分析】观察题干可知,
根据上面的计算可得规律:,据此即可解答问题。
【解答】解:(1)我发现:像上面这种加法的和数,等于中间数乘中间数。
(2)根据规律直接写出下面几题的结果。
。
。
故答案为:中间数,中间数;7,7,49,15,15,225。
【点评】对于此类问题,首先应仔细审题,根据数字特点,得出计算规律再进行解答。
30.【分析】仔细观察式的规律,等式的左边是一个偶数,右边是两个奇质数(质数是奇数)的和,据此解答即可。
【解答】解:根据分析可得:你的猜想是:任何一个大于6的偶数可以表示为两个奇质数之和。
我国数学家陈景润在这一方面做了深入的研究,这种探索和钻研精神非常值得我们同学们学习。1742年,德国数学家哥德巴赫发现了这个规律,这个设想被简称为“”,也就是著名的“哥德巴赫猜想”。请你仿照例子填空:,。(答案不唯一)
【点评】本题主要考查了质数与合数,奇数与偶数的问题,要掌握常见的质数。
第七单元《解决问题的策略》
姓名:_________ 班级:_________ 学号:_________
一、填空题(满分20分)
1.(2分)观察下面的算式:
5×9=45
55×99=5445
555×999=554445
5555×9999=55544445
……
则555555×999999=_________.
2.(2分)小亮用计算器算出了四个算式的结果:7×202=1414,12×202=2424,23×202=4646,36×202=7272。根据这些算式的规律可知45×202=_________。
3.(2分)根据算式的规律填空。
,,, 。
4.(2分),按照这样的规律, 。
5.(2分)5个同样的小长方形拼成一个面积为的大长方形(如图),阴影部分的面积是 。
6.(2分)街心公园里有一种“围树座椅”,形状如图。这种“围树座椅”椅面的面积是 。
7.(2分)非遗文化之手工剪纸。盈盈用一张直径是的圆形纸片剪出如图所示的“风车”图案(空白部分),则被剪掉的纸片(阴影部分)的面积是 。
8.(2分)一种可以折叠的圆形餐桌,桌面直径2米,把四周折叠后就是一个正方形餐桌(如图)。这个餐桌的折叠部分(阴影部分)的面积是 平方米。
9.(2分)已知,,,那么 , 。
10.(2分)根据算式的规律填空:,,在计算中,写出〇、□表示的整数:〇 ,□ 。
二、判断题(满分10分)
11.(2分)如图是由7个同样的正方形拼成的,涂色部分甲与涂色部分乙的面积相等。
12.(2分)如图是三个完全相同的长方形,它们阴影部分的面积相等. .
13.(2分)由,,能推出。
14.(2分)在中,从“1”到数“13”的和是49. .
15.(2分)求下面图形的周长和面积.(单位:厘米.2只求面积)
三、选择题(满分10分)
16.(2分)不计算,用发现的规律得到最后一道题的商是()
?
A.0.2020 B. C. D.
17.(2分)仔细观察下面这组算式:
根据规律接着往下写,第4个算式是()
A. B.
C. D.
18.(2分)根据,那么
A. B. C.
19.(2分)下列各图中的正方形面积相等,图()的阴影面积与另外三图不同.
A. B. C. D.
20.(2分)如图,圆的直径是7厘米,正方形的面积是()平方厘米。
A.21.98 B.10.99 C.49 D.24.5
四、计算题(满分24分)
21.(6分)求如图中阴影部分的面积(图中单位:。
22.(6分)找规律,写得数。
。
23.(6分)先计算,再思考后完成填空.
根据:,,
可以得出:
24.(6分)如图,阴影部分的面积是,求圆环的面积。
五、解答题(满分36分)
25.(6分)淘气在一块梯形空地上挖了一个直径为8米的圆形水池,其余的部分植上草坪,请计算植草坪部分的面积。(单位:米)
26.(6分)太极图在中国传统文化中含义深邃,其形状为阴阳两鱼互纠在一起,象征两极和合。
(1)请你照样子画一个。
(2)如果大圆半径是6厘米,请求出阴鱼(即阴影部分)的面积。
求面积的计算过程是:
27.(6分)如图,一张可折叠的圆桌折叠后成了正方形,如果正方形的边长是1.2米,那么圆桌原来的面积是多少平方米?(结果保留两位小数。
28.(6分)先计算—探究规律,然后运用规律—完成填空。
;
;
;
。
29.(6分)先阅读理解,再解决问题。
有这样的一组算式:
;
;
;
;
(1)我发现:像上面这种加法的和数,等于 乘 。
(2)根据规律直接写出下面几题的结果。
。
。
30.(6分)亲爱的同学们,在小学阶段我们认识了许多新的数,比如质数(素数)、合数、奇数、偶数等。下面的数你能找到其中的规律吗?写出你的猜想。
8=3+5;10=3+7;12=5+7;14=3+11;16=3+13=5+11;18=5+13=7+11
20=3+17=7+13;22=3+19=5+17;24=5+19=7+17=11+13;26=______+______=______+______……你的猜想是:任何一个大于6的偶数可以______。
我国数学家陈景润在这一方面做了深入的研究,这种探索和钻研精神非常值得我们同学们学习。1742年,德国数学家哥德巴赫发现了这个规律,这个设想被简称为“1+1”,也就是著名的“哥德巴赫猜想”。请你仿照例子填空:30=______+______,40=______+______。
参考答案
一、填空题(满分20分)
1.【分析】通过仔细观察,得出规律:n个5×n个9=(n-1)个5,n个4,最后是一个5.因此,当n=6时,据此规律,很快就可写出.
【解答】解:555555×999999=555554444445;
故答案为:555554444445.
【点评】此题属于找规律的题目,解答这类问题,应仔细观察给出的例子,找出规律,据规律解答.
2.【分析】观察四个算式可知,算式的第二个因数都是202,把第一因数乘2的积写2次,即为算式的积。
【解答】解:,所以。
故答案为:9090。
【点评】找出积与因数之间的关系,本题主要考查学生分析归纳能力。
3.【分析】根据,,可以发现的规律,据此解答即可。
【解答】解:,,,。
故答案为:;。
【点评】本题考查了算式的规律,结合题意分析解答即可。
4.【分析】根据,可知,从开始,依次加前面加数的,最后的结果等于1减去最后的分数,按照这样的规律,解答即可。
【解答】解:分析可知,。
故答案为:,。
【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题。
5.【分析】阴影部分的面积占4个长方形面积的一半,先求出1个小长方形的面积再乘4求出4个长方形的面积,最后再除以2即可。
【解答】解:
答:阴影部分的面积是。
故答案为:16。
【点评】本题考查的是组合图形的面积的应用。
6.【分析】根据圆环的面积公式即可解答。
【解答】解:大圆半径:(米
小圆半径:(米
圆环面积
(平方米)
答:这种“围树座椅”椅面的面积是。
故答案为:9.42。
【点评】本题主要考查圆环的面积公式。
7.【分析】根据图示,阴影部分的面积等于半径是(厘米)的圆的面积减去2个半径是(厘米)的圆的面积,据此解答即可。
【解答】解:大圆半径是:
(厘米)
小圆半径是:
(厘米)
(平方厘米)
答:被剪掉的纸片(阴影部分)的面积是157平方厘米。
故答案为:157。
【点评】本题考查了组合图形面积计算知识,结合圆的面积公式解答即可。
8.【分析】阴影部分的面积圆的面积正方形面积,把正方形分成两个完全一样的三角形,每个三角形的底等于圆的直径,每个三角形的高等于圆的半径,根据圆的面积公式:,三角形的面积公式:,把数据代入公式解答。
【解答】解:
(平方米)
答:这个餐桌的折叠部分(阴影部分)的面积是1.14平方米。
故答案为:1.14。
【点评】此题主要考查圆的面积公式、正方形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式。
9.【分析】根据题意,,,,由此发现规律:,据此解答即可。
【解答】解:已知,,,那么,。
故答案为:444444,。
【点评】根据所给的算式,发现规律是,然后利用规律解答即可。
10.【分析】根据题意,,,可以发现如下规律:,据此解答即可。
【解答】解:分析可以发现如下规律:,所以在计算中,写出〇、□表示的整数:〇,□。
故答案为:7;42。
【点评】本题考查了算式中的规律知识,结合题意分析解答即可。
二、判断题(满分10分)
11.【分析】等底等高的三角形面积相等。同样的正方形,则每个正方形的边长相等。甲三角形的底是2个正方形的边长,高是1个正方形的边长。乙三角形是底也是2个正方形的边长,高是1个正方形的边长。结合三角形的面积底高,解答即可。
【解答】解:设正方形的边长为1。
甲三角形的底是2个正方形的边长,高是1个正方形的边长。甲面积:
乙三角形是底也是2个正方形的边长,高是1个正方形的边长。乙面积:
答:涂色部分甲与涂色部分乙的面积相等。所以原题说法正确。
故答案为:。
【点评】本题考查了组合图形面积计算知识,结合三角形的面积公式解答即可。
12.【分析】图中的阴影部分均为三角形,根据三角形的面积公式可知三角形的面积是由三角形的底和高决定的,图中阴影部分的三角形的底相等,高相等,所以面积也相等.
【解答】解:三角形的面积底高,
图中阴影部分的三角形,底相等,高相等,
所以阴影部分的面积也相等.
故判:.
【点评】此题主要考查的是等底等高的三角形的面积也相等.
13.【分析】依据题意可知,利用除法的计算方法计算的商,由此解答本题。
【解答】解:
,本题说法错误。
故答案为:。
【点评】本题从题中算式可知,被除数是几,商的小数部分就是被除数的9倍。
14.【分析】在中首先求出“13”是第几项(由于项数比较少,可能用数的方法),由于相邻两数的差是1,所以项数等于(末项首项),据即可求13是第几项;前项和的计算公式是(末项首项),根据公式可求出前13项的和,根据计算结果进行判断.
【解答】解:在中,从“1”到数“13”的项数为:
前6项的和为:
因此,在中,从“1”到数“13”的和是49,原题的说法是正确的.
故答案为:.
【点评】此题项数较少,写出所有项,通过计算即可得到正确的结果.如果项数较多,只能先总结出求项数、前项和公式解答.
15.【分析】(1)这个图形的周长等于直径2厘米的半圆的弧长与两条2.5厘米和一条2厘米的线段的长度之和,面积等于这个半圆的面积与下面的长方形的面积之和,据此计算即可解答;
(2)阴影部分的面积等于直径10厘米的圆的面积与中间的正方形的面积之差,正方形的面积可以看做两个直角三角形的面积来计算,这两个三角形的底都是10厘米,高都是厘米,所以这个正方形的面积平方厘米,据此计算即可解答.
【解答】解:(1)阴影部分的周长是:
(厘米)
面积是:
(平方厘米)
(2)面积是:
(平方厘米)
【点评】此题主要考查图形的周长和面积,求阴影部分的周长时容易错,关键要理解周长的意义,即围成图形一周的长度.
三、选择题(满分10分)
16.【分析】观察题中算式可知,除数都是99,商是循环小数,循环节是被除数,由此解答本题。
【解答】解:由分析可知,
故选:。
【点评】解决本题的关键是找出题中的规律,利用规律去解答。
17.【分析】根据题目给出的算式发现,每个算式第二个数都是8,第一个数位数依次递增,可以推测第四个式子的第一个数是1234,第三个数依次递加1,可以推测第四个式子的第三个数是4,得数的位数也分别递增,而且第几个式子得数就是几位数,应为9876。
【解答】解:
根据分析,第4个算式是。
故选:。
【点评】此题考查式的规律,找出规律是解决此类题目的关键。
18.【分析】,即是正整数),由此求解。
【解答】解:根据,
那么。
故选:。
【点评】解决本题先从已知的算式中找出规律,再根据规律求解。
19.【分析】从图中可以看出阴影部分的面积正方形的面积圆的面积.观察图形可发现:四个正方形是全等的,面积是相等;、、三个图形中空白部分可以组成一个完整的圆,根据圆的面积相等可得这三个图形中阴影部分的面积相等,得出答案.
【解答】解:由图可知:从左到右、、的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,
根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等.
故选:.
【点评】此题考查了面积及等积变换,将阴影面积转化为易求的图形的面积的差或和是解题的常用方法.
20.【分析】由图可知,图中的大正方形是由4个底和高都等于圆半径的三角形组成,据此计算。
【解答】解:
(平方厘米)
答:正方形的面积是24.5平方厘米。
故选:。
【点评】解答本题的关键是分析出小正方形的底和高与圆的直径之间的关系。
四.计算题(满分24分)
21.【分析】根据图示,阴影部分的面积等于正方形的面积减去半径是(厘米)的圆的面积,根据正方形的面积公式:,圆的面积公式:,解答即可。
【解答】解:半径是:
(厘米)
阴影部分的面积:
(平方厘米)
答:阴影部分的面积是21.5平方厘米。
【点评】本题考查了正方形和圆的面积公式的灵活运用,结合题意分析解答即可。
22.【分析】连加算式的第一个加数都是1,后面的每一个加数都是前面一个加数的2倍,不难发现:这样的连加算式都可以用最后一个加数乘2减1来计算。
【解答】解:
故答案为:63;127;512。
【点评】解决本题的关键是根据数据之间的特征,推理出转化的规律。
23.【分析】各式都是两个分数相减,各分数的分子都是1,分母是从2开始的相邻两个自然数.通过计算可知,两个分数之差的分子是两分母之差,分母是两分母之积.根据这一规律,把中的看作、看作、看作然后即可计算等于几.
【解答】解:,,
.
故答案为:,,,.
【点评】解答此题的关键是根据前面的三个算式摸出此类分数相减的规律,然后再把下面一个算式的各分数分解成两个分数之差,然后即可进行计算.
24.【分析】根据阴影部分的面积为大三角形的面积减去小三角形的面积,大三角形的面积等于大圆半径的平方除以2,小三角形面积同理即可解答。
【解答】解:
(平方厘米)
圆环面积:(平方厘米)
答:圆环的面积是1256平方厘米。
【点评】本题主要考查阴影部分的面积为大三角形的面积减去小三角形的面积。
五.解答题(满分36分)
25.【分析】根据图示,草坪部分的面积等于梯形的面积减去直径为8米的圆形水池面积,据此解答即可。
【解答】解:
(平方米)
答:草坪部分的面积是173.76 平方米。
【点评】本题考查了组合图形面积计算知识,结合题意分析解答即可。
26.【分析】(1)画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
据此先画出一个大圆,在大圆中画出一条竖直的直径,分别以两条半径的中点为圆心,向右和向左画出两个半圆,再以两个半圆的圆心为圆心分别画出两个小圆即可,据此作图。
(2)根据图示,阴鱼的面积大圆面积的一半,根据圆的面积圆周率半径的平方,求出大圆面积,除以2即可。
【解答】解:(1)照样子画一个,如图:
(2)
(平方厘米)
答:如果大圆半径是6厘米,阴鱼的面积是56.52平方厘米。
【点评】此题主要考查了圆的画法以及圆的面积公式的灵活运用,关键是熟记公式。
27.【分析】设圆桌的半径是米,圆桌的直径等于正方形的对角线的长,根据“正方形的面积边长边长正方形对角线的长对角线长的一半”,据此求出半径的平方,再根据“圆的面积半径的平方”解答。
【解答】解:设圆桌的半径是米。
(平方米)
答:那么圆桌原来的面积大约是2.26平方米。
【点评】根据“正方形的面积边长边长正方形对角线的长对角线长的一半”求出圆桌的半径的平方是解题的关键。
28.【分析】根据异分母分数加法的计算方法,求出第一个算式的结果,发现结果的分母与最后一个加数的分母相同,分子比分母少1,后边都是这个规律;到最后一个算式,,加,结果就是1,据此分析解答即可。
【解答】解:
故答案为:;;;。
【点评】本题考查了算式的规律知识,结合题意找出规律,然后分析解答即可。
29.【分析】观察题干可知,
根据上面的计算可得规律:,据此即可解答问题。
【解答】解:(1)我发现:像上面这种加法的和数,等于中间数乘中间数。
(2)根据规律直接写出下面几题的结果。
。
。
故答案为:中间数,中间数;7,7,49,15,15,225。
【点评】对于此类问题,首先应仔细审题,根据数字特点,得出计算规律再进行解答。
30.【分析】仔细观察式的规律,等式的左边是一个偶数,右边是两个奇质数(质数是奇数)的和,据此解答即可。
【解答】解:根据分析可得:你的猜想是:任何一个大于6的偶数可以表示为两个奇质数之和。
我国数学家陈景润在这一方面做了深入的研究,这种探索和钻研精神非常值得我们同学们学习。1742年,德国数学家哥德巴赫发现了这个规律,这个设想被简称为“”,也就是著名的“哥德巴赫猜想”。请你仿照例子填空:,。(答案不唯一)
【点评】本题主要考查了质数与合数,奇数与偶数的问题,要掌握常见的质数。
