5.4函数的奇偶性 课件(共33张PPT)
文档属性
| 名称 | 5.4函数的奇偶性 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-11 00:00:00 | ||
图片预览





文档简介
(共33张PPT)
5.4函数的奇偶性
年 级:高一年级 学 科:数学(苏教版)
轴对称
中心对称
对称是一个广阔的主题,在艺术和自然两个方面意义重大,数学则是它的根本。
——赫尔曼·外尔
(德国数学家、物理学家)
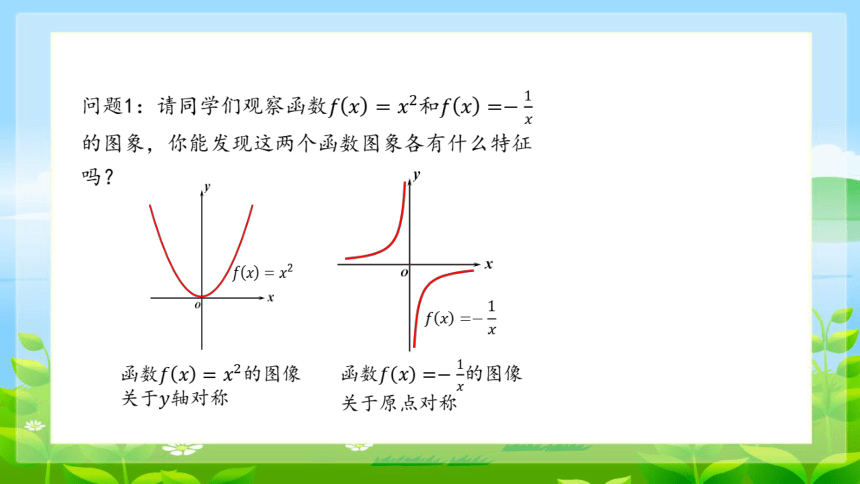
问题1:请同学们观察函数和 的图象,你能发现这两个函数图象各有什么特征吗?
函数的图像关于轴对称
函数的图像关于原点对称
数缺形时少直观,形少数时难入微
——华罗庚
(中国科学院院士、数学家)
这启发了我们可以从数量关系角度来精准刻画这两种对称
追问:如何精准刻画函数图象的这两种对称性呢?
A
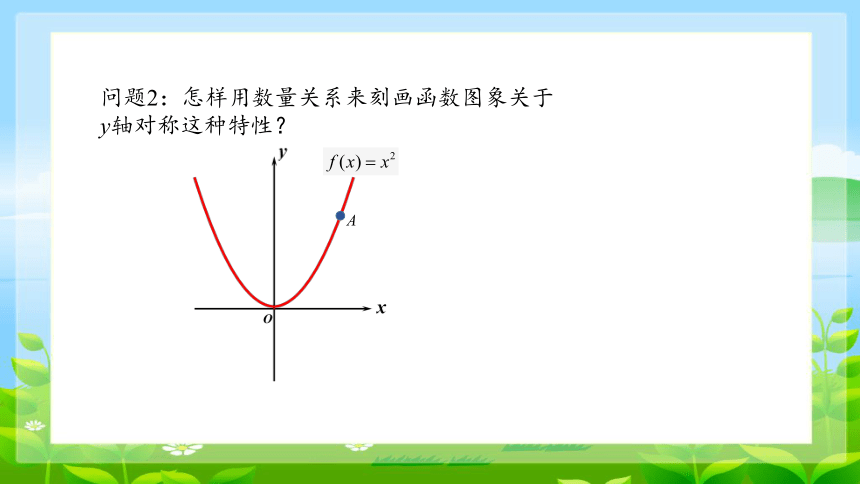
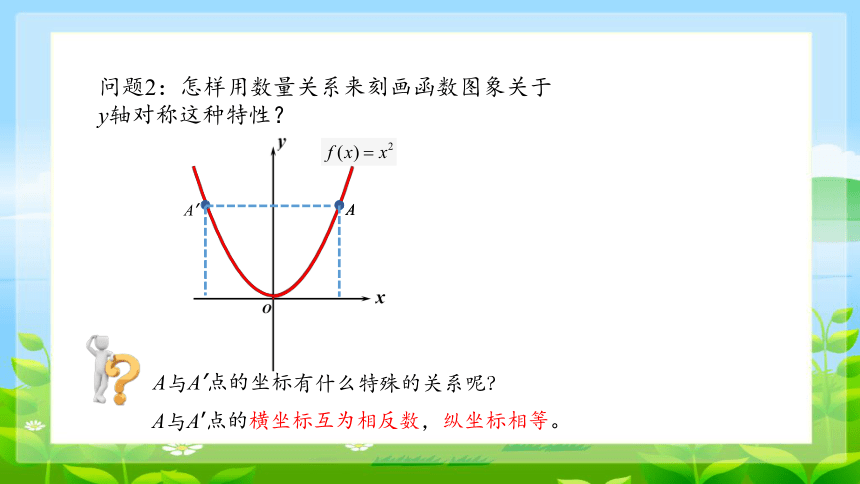
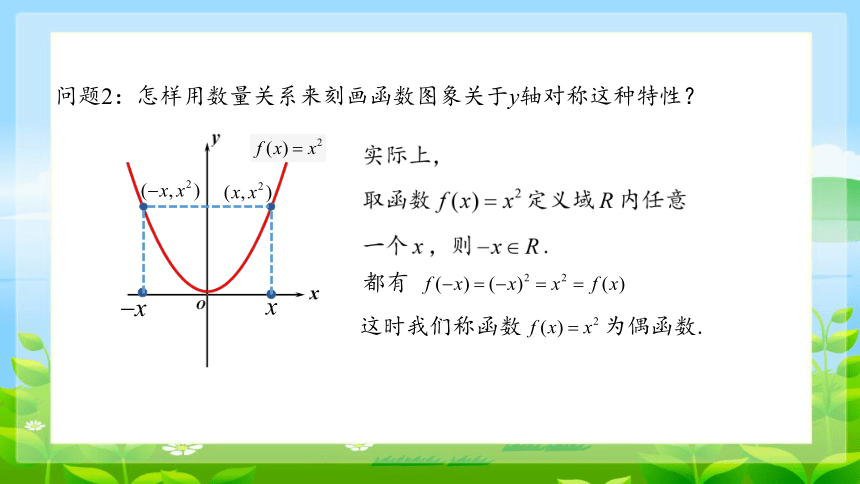
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
A与A’点的坐标有什么特殊的关系呢?
A
A
A’
A与A’点的横坐标互为相反数,纵坐标相等。
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
… …
… …
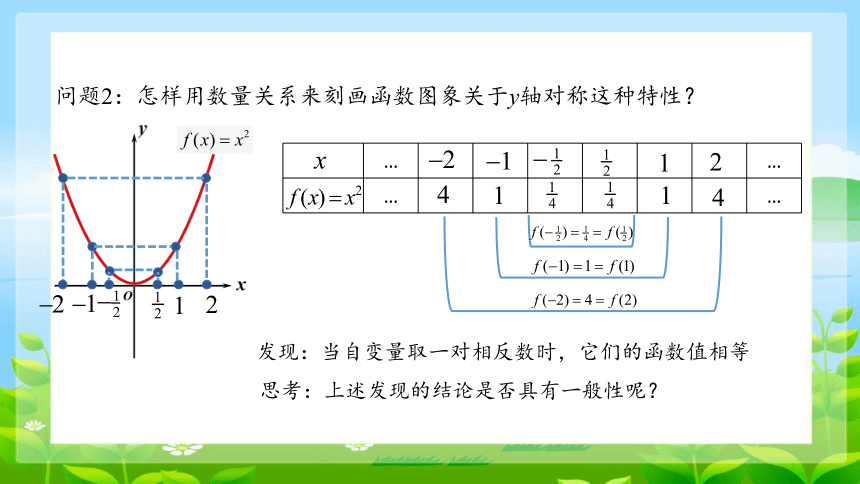
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
发现:当自变量取一对相反数时,它们的函数值相等
思考:上述发现的结论是否具有一般性呢?
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
都有
这时我们称函数 为偶函数.
根据偶函数定义可知:偶函数的图象关于y轴对称; 反之,一个函数的图象关于y轴对称,那么这个函数是偶函数.
函数 是偶函数的充要条件是它的图象关于y轴对称.
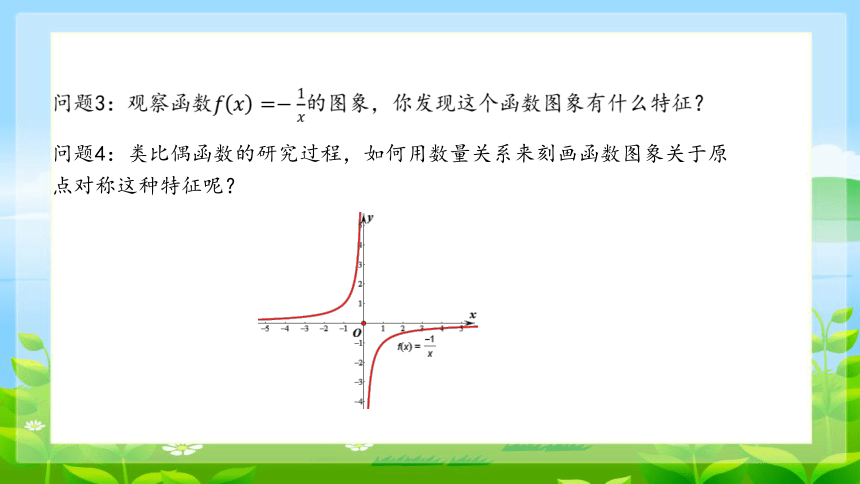
问题3:观察函数的图象,你发现这个函数图象有什么特征?
问题4:类比偶函数的研究过程,如何用数量关系来刻画函数图象关于原点对称这种特征呢?
… …
… …
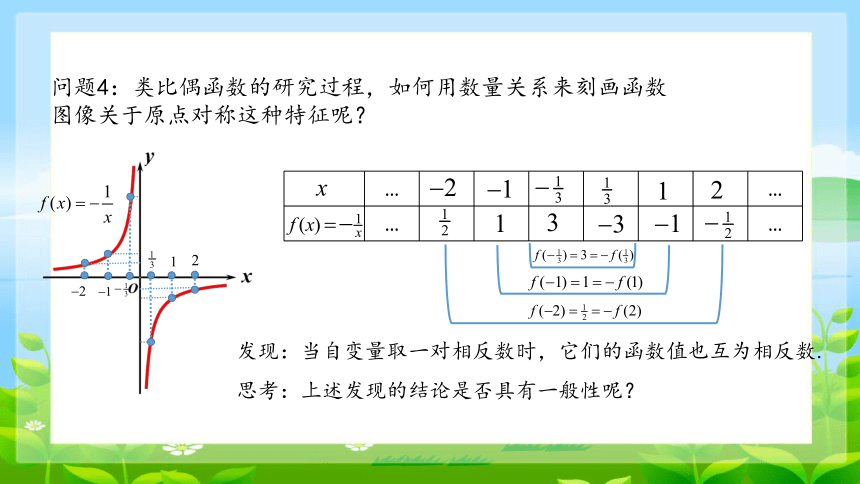
发现:当自变量取一对相反数时,它们的函数值也互为相反数.
思考:上述发现的结论是否具有一般性呢?
问题4:类比偶函数的研究过程,如何用数量关系来刻画函数图像关于原点对称这种特征呢?
都有
这时我们称函数 为奇函数.
问题4:类比偶函数的研究过程,如何用数量关系来刻画函数图像关于原点对称这种特征呢?
A
A’
根据奇函数定义可知:奇函数的图象关于原点对称; 反之,一个函数的图象关于原点对称,那么这个函数是奇函数.
函数是奇函数的充要条件是它的图象关于原点对称
思考:如何理解奇(偶)函数定义中“任意A,都有A”这句符号语言的含义?
思考:如何理解“任意A,都有A”这句符号语言的含义?
1.说明与同在定义域中;
也说明:奇偶函数定义域是关于原点对称;
进一步说明:定义域关于原点对称是函数具有奇偶性的必要不充分条件.
2.说明要取遍定义域中的每一个值;
也说明:奇偶性是函数的整体性质.
3.体现了数学符号语言的简洁和严谨;
相同点 不同点
1.定义域都关于原点对称
2.奇偶性都是函数的整体性质
2.(从图象角度)偶函数的图象关于轴对称,而奇函数的图象关于原点对称.
1.(从数量关系角度)当自变量取一对相反数时,偶函数的函数值相等(即),而奇函数的函数值是一对相反数(即).
思考:奇偶函数的相同点和不同点有哪些?
例1 判定下列函数是否为偶函数或奇函数:
解:(1)函数的定义域为R.
因为对于任意R,都有R,
且,
所以,函数为偶函数
例1 判定下列函数是否为偶函数或奇函数:
解:(2)函数的定义域为R.
因为对于任意R,都有R,
所以,函数为奇函数
且,
例1 判定下列函数是否为偶函数或奇函数:
(1)函数的定义域为R.
因为对于任意R,都有R,
且,
所以,函数为偶函数
(2)函数的定义域为R.
因为对于任意R,都有R,
所以,函数为奇函数
且,
第一步:
求定义域,并判断定义域是否关于原点对称.
第二步:
计算,判断与的关系.
第三步:
根据奇偶性的定义作结论
思考:用定义判断函数奇偶性的步骤是什么?
解:(3)函数的定义域为R.
因为对于任意R,都有R,
所以,函数为偶函数
且,
例1 判定下列函数是否为偶函数或奇函数:
解:(4)函数定义域为R.
因为,,所以
,,
因此,根据函数奇偶性定义可以知道,函数既不是奇函数,也不是偶函数.
例1 判定下列函数是否为偶函数或奇函数:
观察例1中四个函数图象,并判断函数的奇偶性.
偶函数
奇函数
偶函数
既不是奇函数,
也不是偶函数
(1)
(2)
(3)
(4)
利用图象的对称性可以快速、直观的判断函数的奇偶性
观察下面两个函数图象,并判断函数奇偶性.
既不是奇函数,
也不是偶函数
判断函数奇偶性的前提:判断函数定义域是否关于原点对称.
1
-1
既是奇函数,
也是偶函数
(2)
(1)
例2 判定函数是否具有奇偶性.
解:函数的定义域为R.
因为对于任意R,都有R,且
所以,函数为奇函数.
问题5:研究奇(偶)函数的好处是什么?
研究奇偶性好处───简化对函数的认识过程
部分
整体
函数图象
图象特征(对称性)
数量刻画
符号语言
抽象定义
1.函数奇偶性的研究方法:
奇偶性判断
课堂总结:
函数奇偶性的定义
判断(证明)
函数奇偶性的方法
图象法
定义法
1、求函数定义域,并判断函数定义域是否关于原点对称
3、根据奇偶性的定义作出结论
2、计算,并判断与的关系.
2.奇偶函数的定义和判断函数奇偶性的方法:
根据奇偶函数图象对称特征作出判断
课堂总结:
3.本节课用到的两个重要的数学思想:
①数形结合思想
②特殊与一般思想
课堂总结:
课后作业
【基础巩固】(必做)
教材118—119页练习4、5、6
【能力提升】(必做)
已知函数为奇函数且定义域为R,时,,求的解析式.
【探究发现】(选做)
函数的图象关于直线对称,你能用数量关系来刻画图象的这种对称性吗?
新的数学方法和概念,常常比解决数学问题本身更重要。
——华罗庚
(中国科学院院士、数学家)
5.4函数的奇偶性
年 级:高一年级 学 科:数学(苏教版)
轴对称
中心对称
对称是一个广阔的主题,在艺术和自然两个方面意义重大,数学则是它的根本。
——赫尔曼·外尔
(德国数学家、物理学家)
问题1:请同学们观察函数和 的图象,你能发现这两个函数图象各有什么特征吗?
函数的图像关于轴对称
函数的图像关于原点对称
数缺形时少直观,形少数时难入微
——华罗庚
(中国科学院院士、数学家)
这启发了我们可以从数量关系角度来精准刻画这两种对称
追问:如何精准刻画函数图象的这两种对称性呢?
A
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
A与A’点的坐标有什么特殊的关系呢?
A
A
A’
A与A’点的横坐标互为相反数,纵坐标相等。
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
… …
… …
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
发现:当自变量取一对相反数时,它们的函数值相等
思考:上述发现的结论是否具有一般性呢?
问题2:怎样用数量关系来刻画函数图象关于y轴对称这种特性?
都有
这时我们称函数 为偶函数.
根据偶函数定义可知:偶函数的图象关于y轴对称; 反之,一个函数的图象关于y轴对称,那么这个函数是偶函数.
函数 是偶函数的充要条件是它的图象关于y轴对称.
问题3:观察函数的图象,你发现这个函数图象有什么特征?
问题4:类比偶函数的研究过程,如何用数量关系来刻画函数图象关于原点对称这种特征呢?
… …
… …
发现:当自变量取一对相反数时,它们的函数值也互为相反数.
思考:上述发现的结论是否具有一般性呢?
问题4:类比偶函数的研究过程,如何用数量关系来刻画函数图像关于原点对称这种特征呢?
都有
这时我们称函数 为奇函数.
问题4:类比偶函数的研究过程,如何用数量关系来刻画函数图像关于原点对称这种特征呢?
A
A’
根据奇函数定义可知:奇函数的图象关于原点对称; 反之,一个函数的图象关于原点对称,那么这个函数是奇函数.
函数是奇函数的充要条件是它的图象关于原点对称
思考:如何理解奇(偶)函数定义中“任意A,都有A”这句符号语言的含义?
思考:如何理解“任意A,都有A”这句符号语言的含义?
1.说明与同在定义域中;
也说明:奇偶函数定义域是关于原点对称;
进一步说明:定义域关于原点对称是函数具有奇偶性的必要不充分条件.
2.说明要取遍定义域中的每一个值;
也说明:奇偶性是函数的整体性质.
3.体现了数学符号语言的简洁和严谨;
相同点 不同点
1.定义域都关于原点对称
2.奇偶性都是函数的整体性质
2.(从图象角度)偶函数的图象关于轴对称,而奇函数的图象关于原点对称.
1.(从数量关系角度)当自变量取一对相反数时,偶函数的函数值相等(即),而奇函数的函数值是一对相反数(即).
思考:奇偶函数的相同点和不同点有哪些?
例1 判定下列函数是否为偶函数或奇函数:
解:(1)函数的定义域为R.
因为对于任意R,都有R,
且,
所以,函数为偶函数
例1 判定下列函数是否为偶函数或奇函数:
解:(2)函数的定义域为R.
因为对于任意R,都有R,
所以,函数为奇函数
且,
例1 判定下列函数是否为偶函数或奇函数:
(1)函数的定义域为R.
因为对于任意R,都有R,
且,
所以,函数为偶函数
(2)函数的定义域为R.
因为对于任意R,都有R,
所以,函数为奇函数
且,
第一步:
求定义域,并判断定义域是否关于原点对称.
第二步:
计算,判断与的关系.
第三步:
根据奇偶性的定义作结论
思考:用定义判断函数奇偶性的步骤是什么?
解:(3)函数的定义域为R.
因为对于任意R,都有R,
所以,函数为偶函数
且,
例1 判定下列函数是否为偶函数或奇函数:
解:(4)函数定义域为R.
因为,,所以
,,
因此,根据函数奇偶性定义可以知道,函数既不是奇函数,也不是偶函数.
例1 判定下列函数是否为偶函数或奇函数:
观察例1中四个函数图象,并判断函数的奇偶性.
偶函数
奇函数
偶函数
既不是奇函数,
也不是偶函数
(1)
(2)
(3)
(4)
利用图象的对称性可以快速、直观的判断函数的奇偶性
观察下面两个函数图象,并判断函数奇偶性.
既不是奇函数,
也不是偶函数
判断函数奇偶性的前提:判断函数定义域是否关于原点对称.
1
-1
既是奇函数,
也是偶函数
(2)
(1)
例2 判定函数是否具有奇偶性.
解:函数的定义域为R.
因为对于任意R,都有R,且
所以,函数为奇函数.
问题5:研究奇(偶)函数的好处是什么?
研究奇偶性好处───简化对函数的认识过程
部分
整体
函数图象
图象特征(对称性)
数量刻画
符号语言
抽象定义
1.函数奇偶性的研究方法:
奇偶性判断
课堂总结:
函数奇偶性的定义
判断(证明)
函数奇偶性的方法
图象法
定义法
1、求函数定义域,并判断函数定义域是否关于原点对称
3、根据奇偶性的定义作出结论
2、计算,并判断与的关系.
2.奇偶函数的定义和判断函数奇偶性的方法:
根据奇偶函数图象对称特征作出判断
课堂总结:
3.本节课用到的两个重要的数学思想:
①数形结合思想
②特殊与一般思想
课堂总结:
课后作业
【基础巩固】(必做)
教材118—119页练习4、5、6
【能力提升】(必做)
已知函数为奇函数且定义域为R,时,,求的解析式.
【探究发现】(选做)
函数的图象关于直线对称,你能用数量关系来刻画图象的这种对称性吗?
新的数学方法和概念,常常比解决数学问题本身更重要。
——华罗庚
(中国科学院院士、数学家)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
